- グループ名ボタンをクリックで各グループ一覧にジャンプします。
- 左にあるA~Cは重要度で、Aが一番重要度の高いコンポーネントになります。
- 「詳しい機能を見る」をクリックで詳細説明が開きます。
- *は書籍『Rhino×Grasshopper All in 1 パーフェクトリファレンス』に記載しているコンポーネントです。

Analysis
Control Points*
B

Curve>Analysis
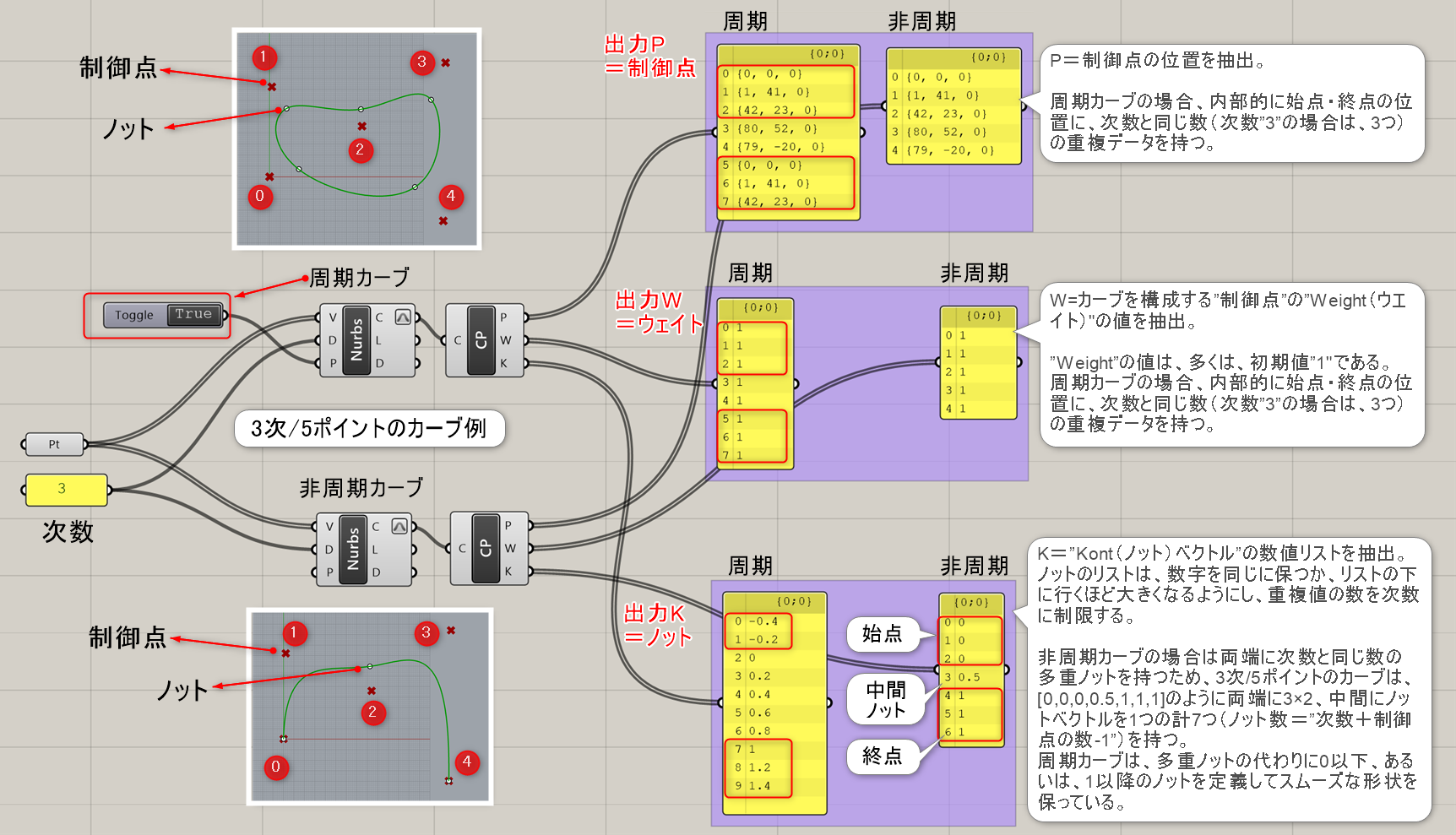
曲線(Curve)を入力し、曲線の制御点(Points)、ウェイト(Weights)、ノットの値(Knots)をそれぞれ出力する。
Control Polygon
C


Curve>Analysis
曲線(Curve)を入力し、制御点(Point)と制御点を繋いだポリライン(PolyLine)を出力する。
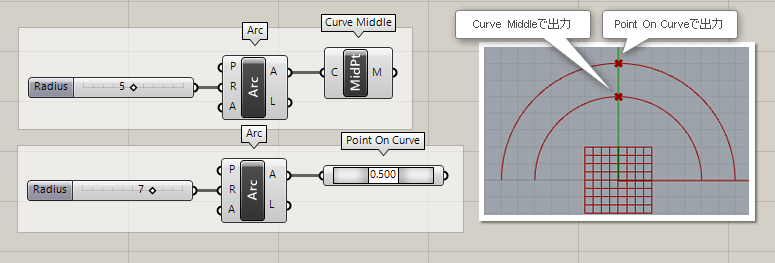
Curve Middle*
B


Curve>Analysis
曲線(Curve)を入力し、その中点(MidPoint)を出力する。
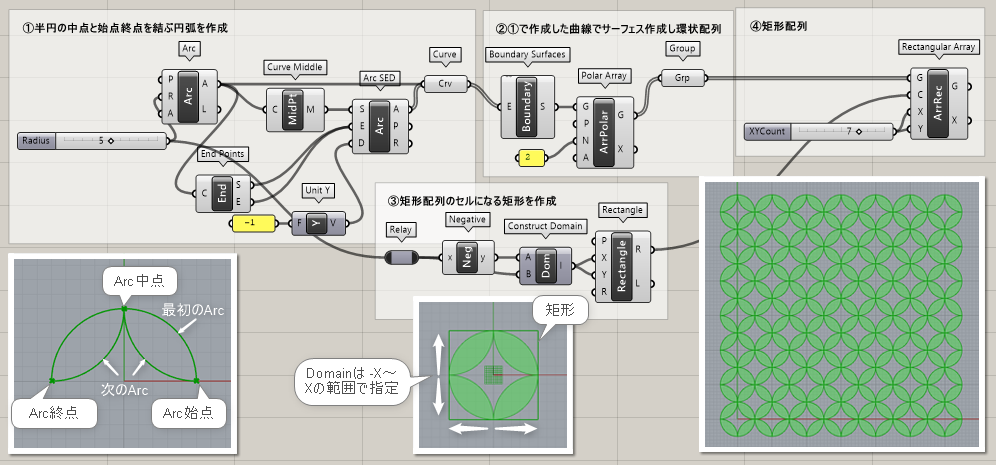
詳細1:C端子に曲線を入力して、M端子から中点を出力する。Point On Curve の0.5と同じ機能。
詳細2:半円の中点と始点終点を使ってモチーフを作成し、矩形配列でパターン化した例。
①半円の中点と始点終点を結ぶ円弧を作成
②Boudary Surfeceでサーフェス作成、Polar Arrayで環状配列
③矩形配列のため、②のモチーフが入る矩形を作成、半径を-X~Xになるように設定
④Recutangrer Arayで矩形配列、パターンを作成
Deconstruct Arc
C
Curve>Analysis
円弧(Arc)を入力し、円弧が描かれた平面(Plane)、半径(Radius)と角度(Angle)を出力する。Arcコンポーネントの反対の効果。
Deconstruct Rectangle*
C
Curve>Analysis
矩形(Rectangle)を入力し、平面(Plane)とX・Y方向の範囲(Domain)をそれぞれ出力する。
End Points*
B


Curve>Analysis
曲線(Curve)を入力し、始点(Start)・終点(End)をそれぞれ出力する。 曲線の向きは、Flip Curveコンポーネントなどで修正可能。
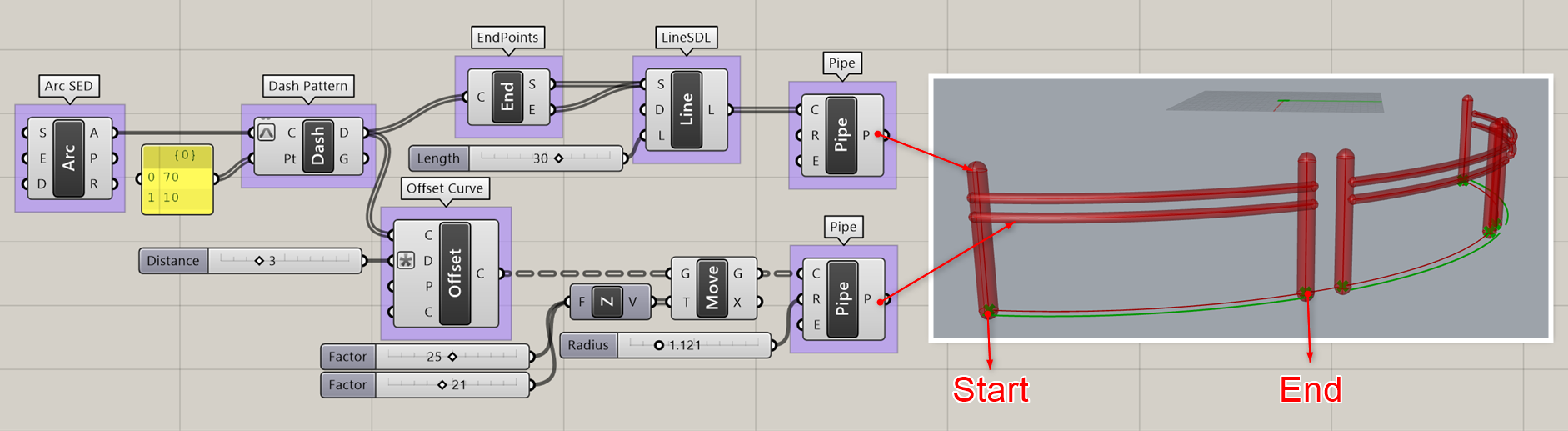
詳細1:カーブの始点・終点を抽出する。閉じたカーブに使用すれば、つなぎ目を取得できる。図は、カーブに対して[Dash Pattern] で作成した隙間のあるカーブ群に対し[End Points]でその両端に支柱を配置し、ガードレールを作成した例。
Polygon Center
C

Curve>Analysis
ポリライン(PolyLine)を入力し、その中心となる点を出力する。Cvは頂点の、Ceはエッジの、Caは面積の中心点を出力する。
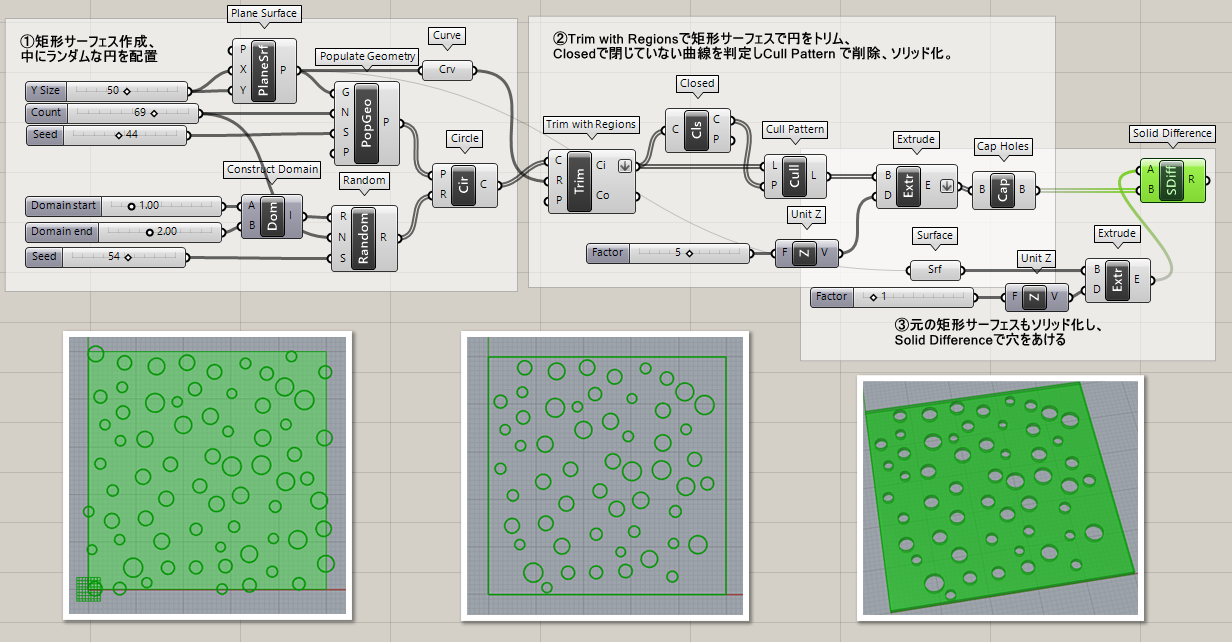
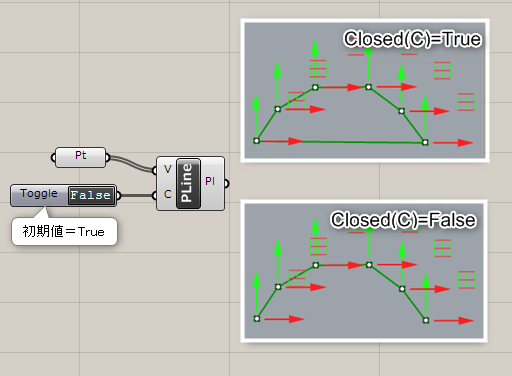
Closed*
B


Curve>Analysis
曲線(Curve)を入力し、閉じているかどうか(Close)、周期曲線(Periodic)かどうかをTrue・Falseで出力する。
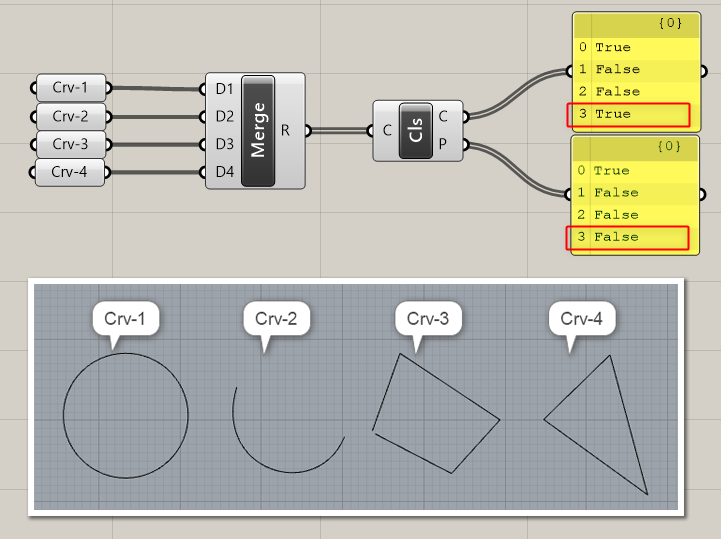
詳細1:カーブを入力すると、
C出力端子:閉じている/閉じていない
P出力端子:周期曲線である/周期曲線でない
をTrue/Falseで出力する。
周期曲線は「キンク(折れ目)のない閉じた曲線」のことである。この例ではCrv-4は閉じてはいるが、キンクがあるため周期曲線ではない。
詳細2:下図はClosedを用いて外形と重なるオブジェクトを削除した例。
①矩形サーフェスの中にランダムな円を作成
②矩形外形よりはみ出している円をトリム後、Closedで閉じていない曲線を判定しCull Patternで削除し、閉じた曲線のみソリッド化
③①の矩形サーフェスもソリッド化、②とのSolid Differenceで穴を抜いてパンチングメタルを作成
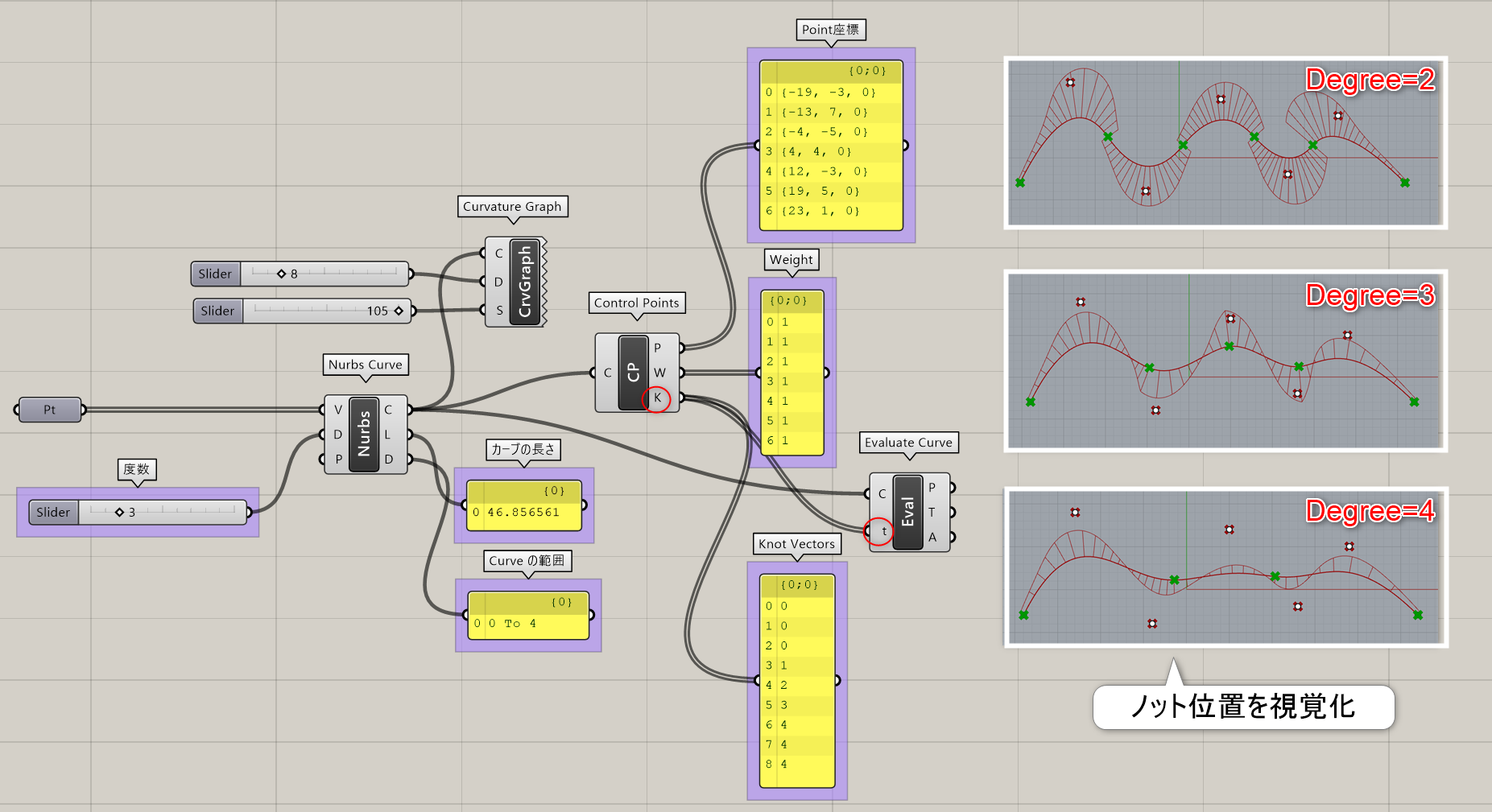
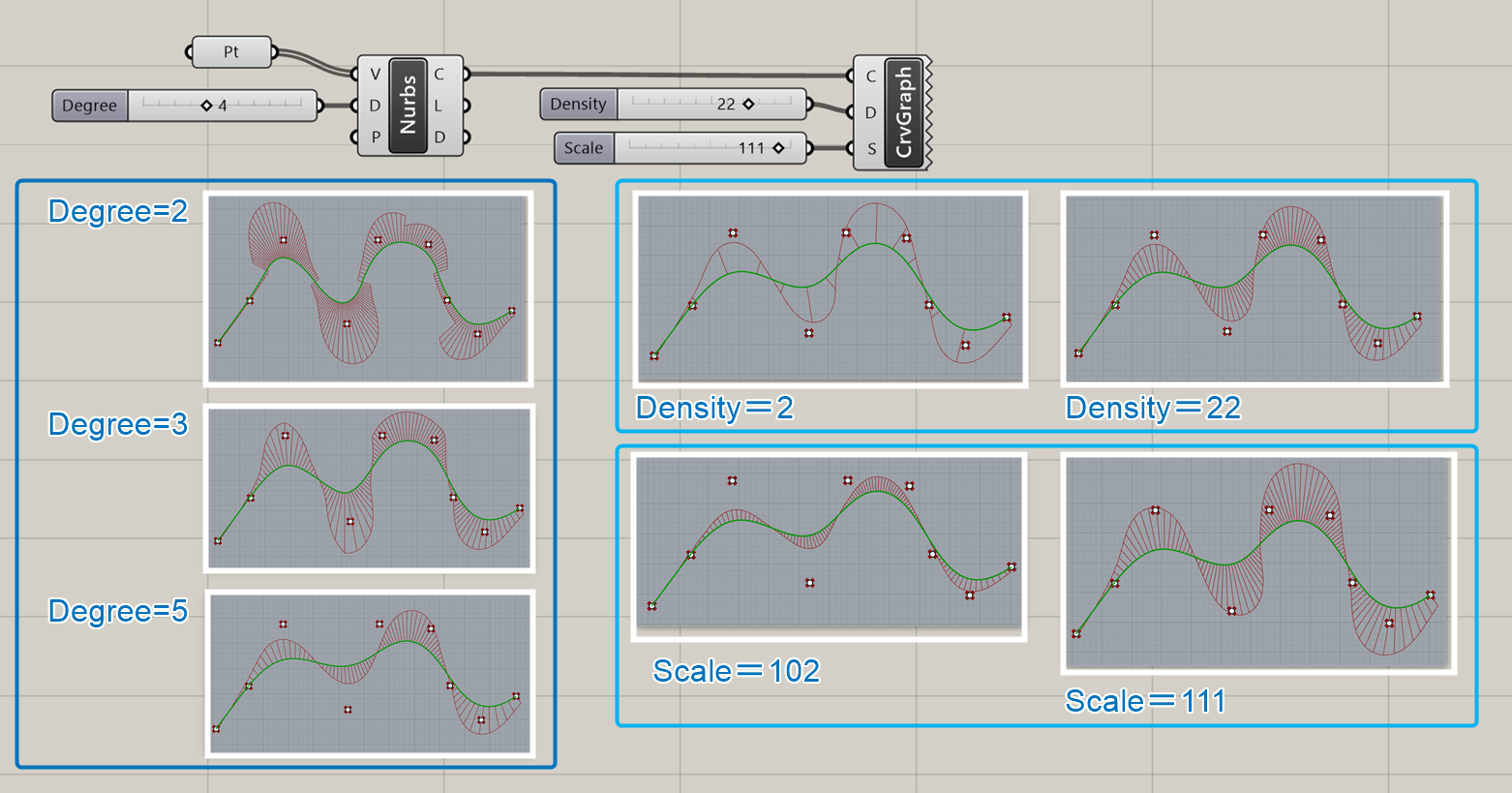
Curvature Graph*
詳細1:曲線(Curve)と密度(Density)、大きさ(Scale)を指定し、曲線の曲率を表示する。図はポイントから作成した[Nurbs Curve]の曲率を次数を変えて[CurvatureGraph]で表示し、密度や大きさを変更した例。
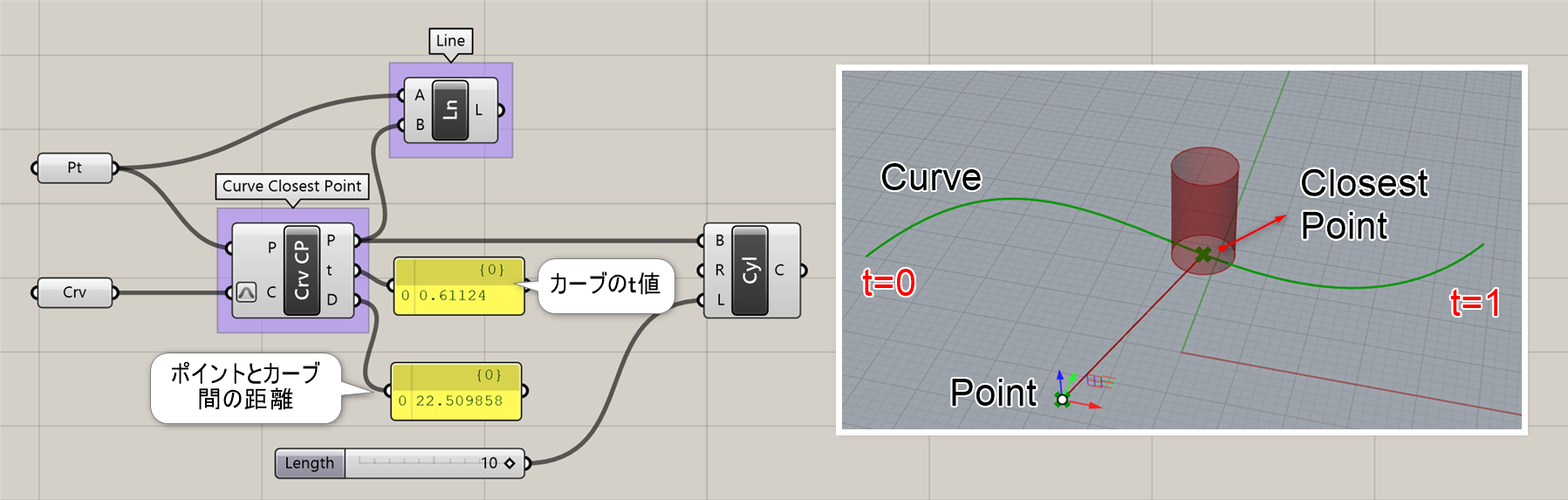
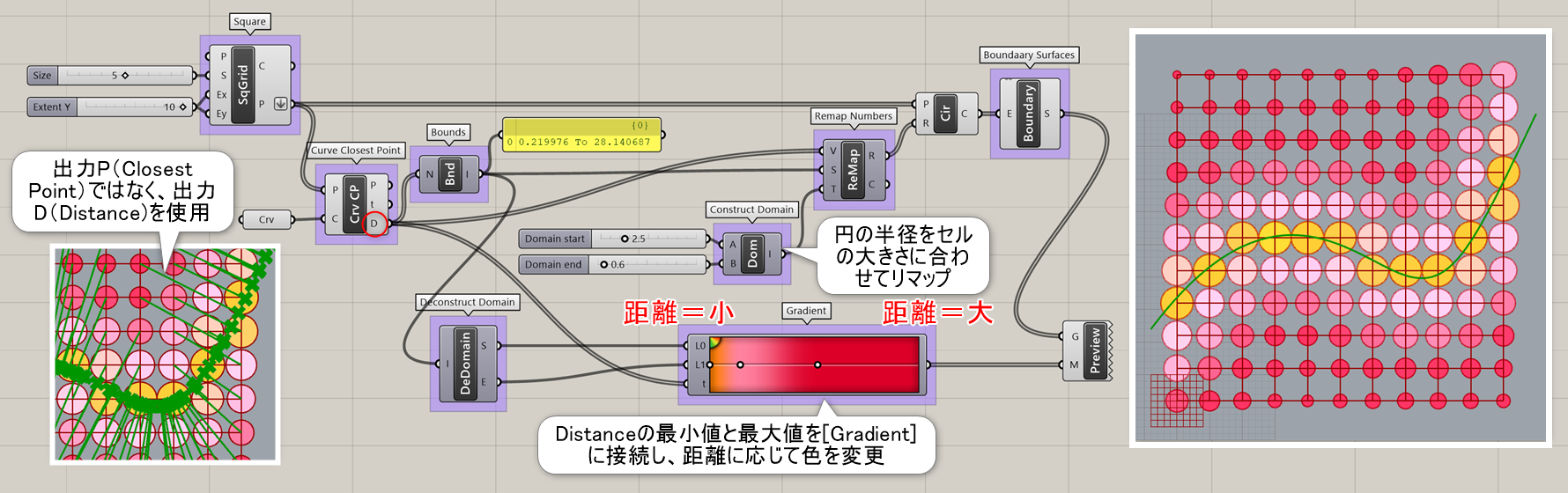
Curve Closest Point
B
Curve>Analysis
点(Point)と曲線(Curve)を入力し、曲線上の最も近い点(Point)を出力する。また該当の箇所のtパラメータ値、移動した距離(Distance)も出力される。
Curve Nearest Object
C
Curve>Analysis
曲線(Curve)と複数のジオメトリ(Geometry)を入力し、曲線に最も近いジオメトリのインデックス(Index)を出力する。また点Aからは曲線上の最も近い点、点Bからはジオメトリ上の最も近い点が出力される。
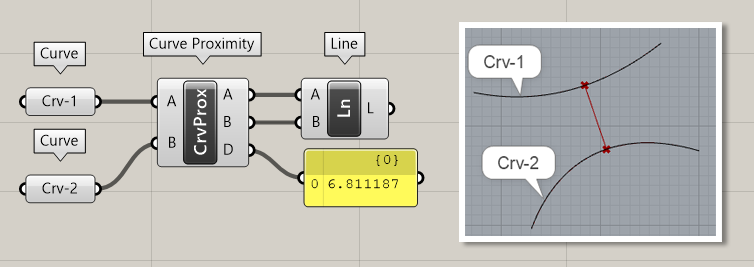
Curve Proximity*
B
Curve>Analysis
曲線A・Bを入力し、それぞれの曲線に最も近い箇所に点(Point)を作成する。またその距離(Distance)も出力する。
Curve Side
C


Curve>Analysis
曲線(Curve)と点(Point)を入力し、左右のどちら側にあるのかを出力する。Sideからは、-1が左、0が曲線上、1が右。LとRからはTrue・Falseで出力される。
Discontinuity*
B

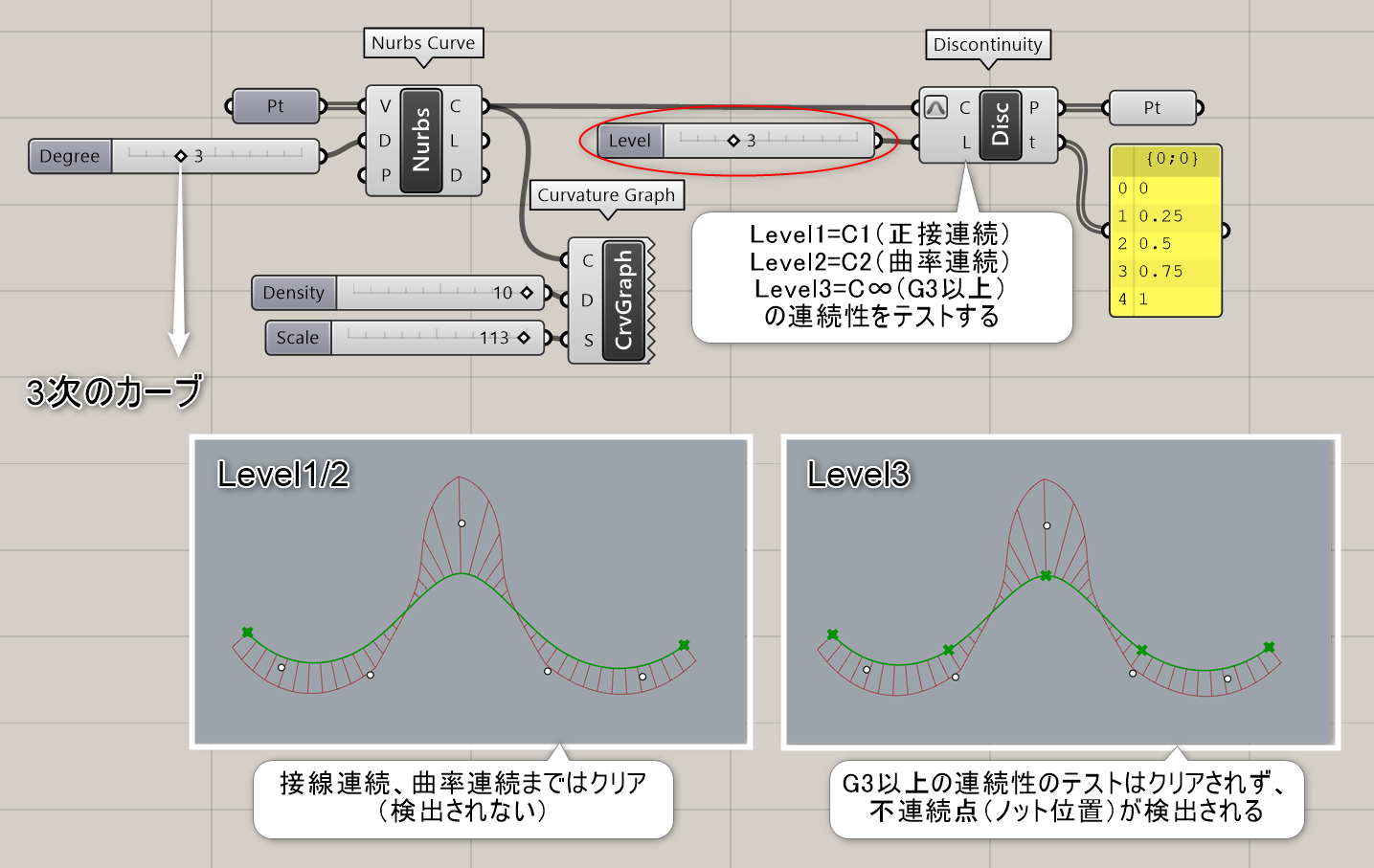
Curve>Analysis
曲線(Curve)と連続性の段階(Level)を指定することで、該当箇所の点(Points)とtパラメータ値を出力する。Levelは1は正接連続、2は曲率連続、3はG3以上の箇所が該当箇所になる。
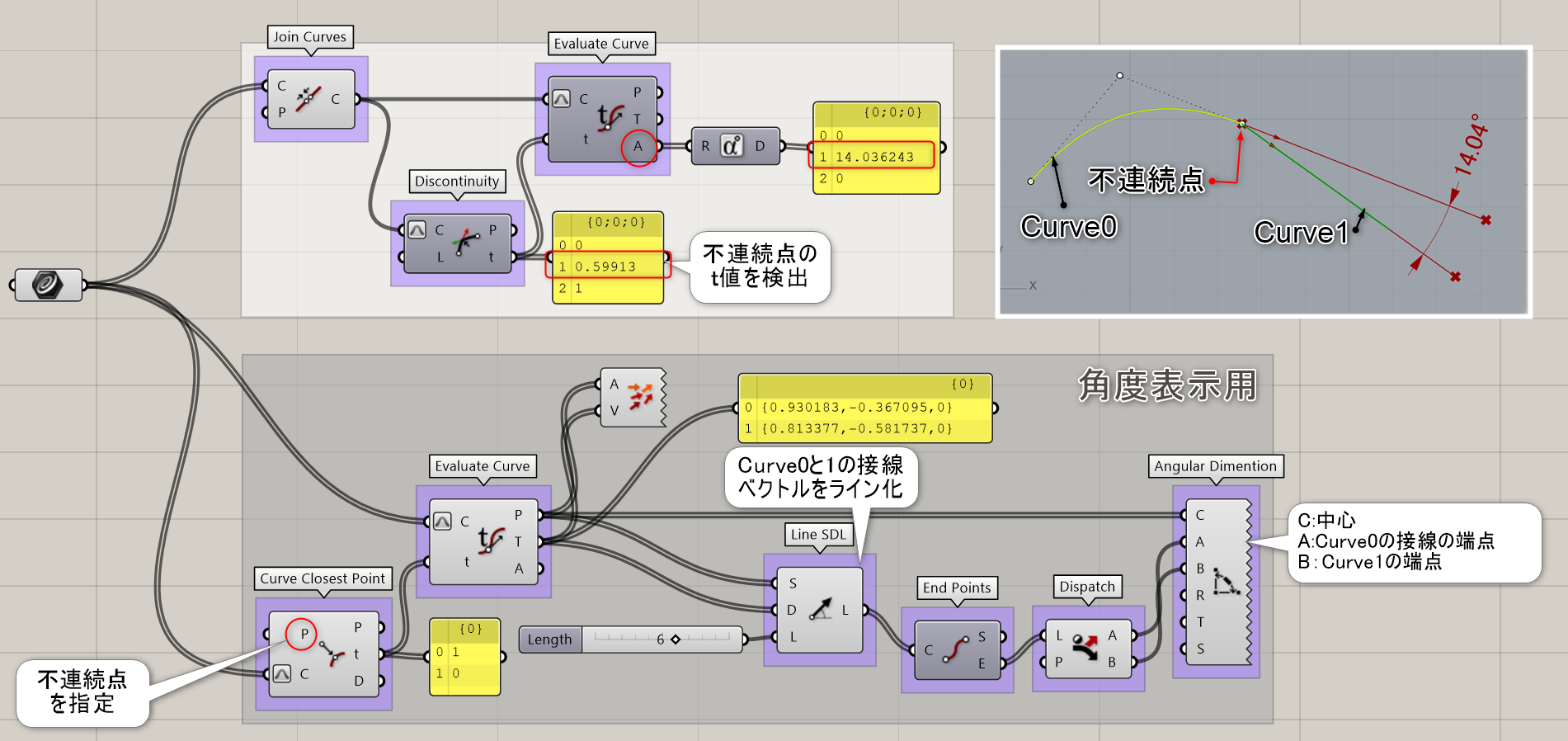
詳細1:曲線(Curve)とテストする連続性の段階(Level)を指定し、レベルごとの不連続点(Points)とtパラメータ値を出力する。Level1=C1は正接連続、2=C2は曲率連続、3=C∞はG3以上の箇所が該当箇所になる。
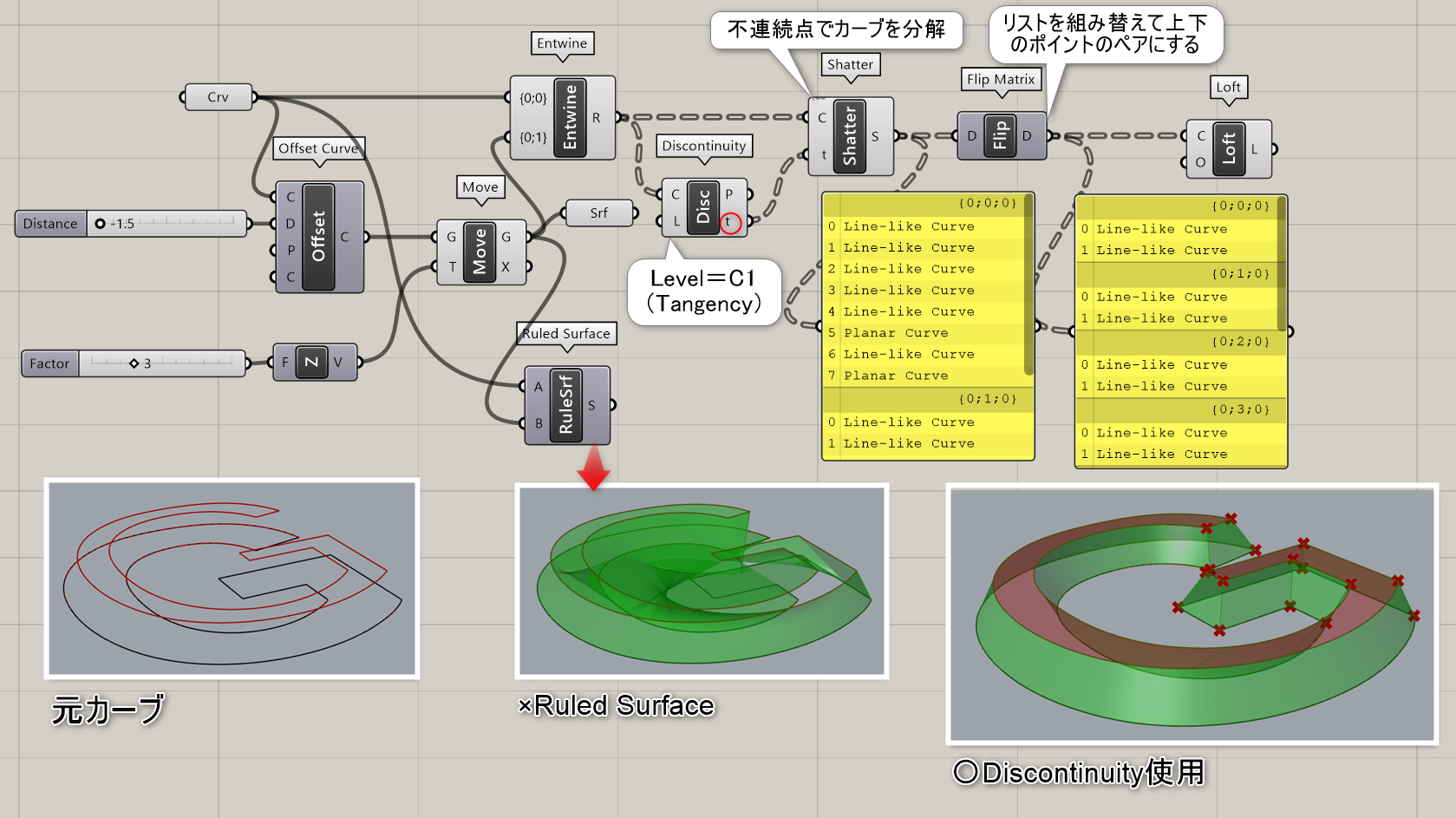
詳細2:オフセットした上下のカーブ間にサーフェスを貼る場合、[Ruled Surface]や[Loft]ではうまくゆかないカーブに対し、[Discontinuity]で検出した不連続点のt値を利用して[Shatter]で分割し、[Flip Matrix]でリストを組み替えてロフト面を生成した例。
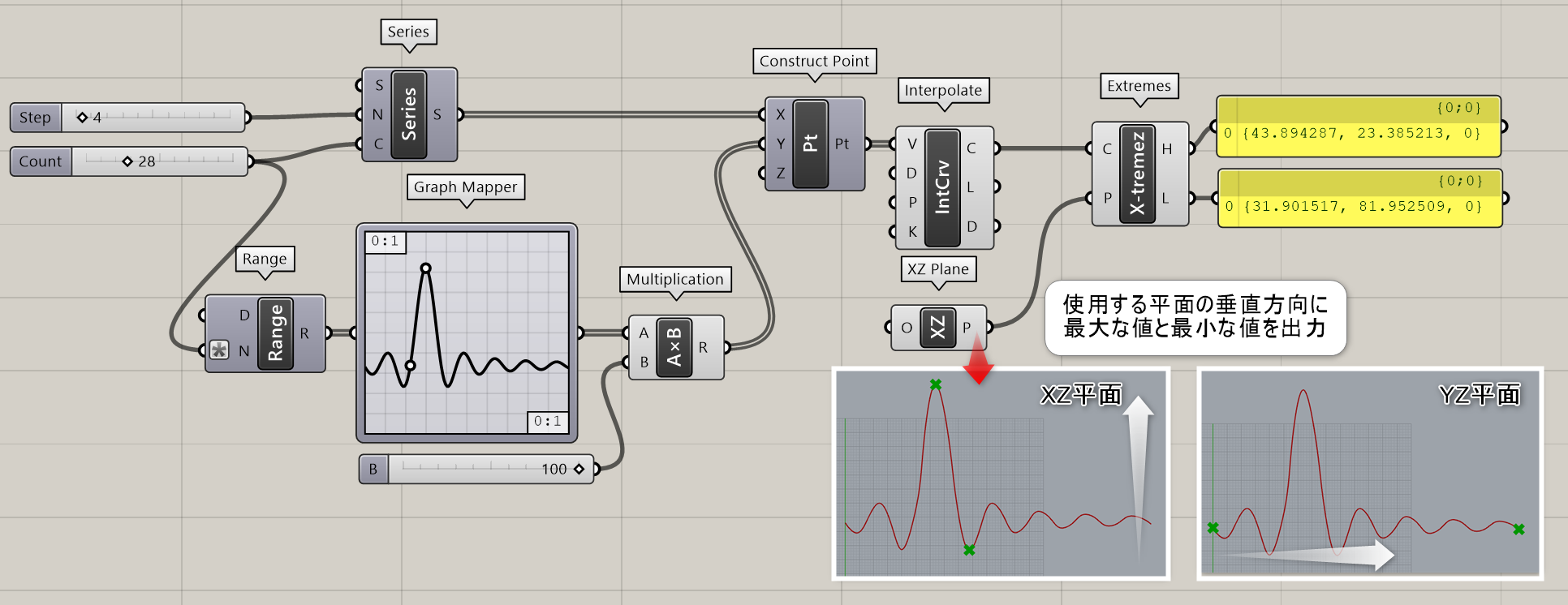
Extremes*
B
Curve>Analysis
曲線(Curve)と平面(Plane)を入力し、平面の垂直方向に最大(Highest)と最小(Lowest)となる点をそれぞれ出力する。(平面の水平ではなく垂直方向に注意すること)
詳細1:曲線(Curve)と平面(Plane)を入力し、平面の垂直方向に最大(Highest)と最小(Lowest)となる点をそれぞれ出力する。平面の水平ではなく垂直方向になるので注意すること。図は、[Graph Mapper]で作成したグラフに対し、[XZ平面]で最大/最小値を出力した例。
また、Math>Utilにも同名の[Extremes]が存在するので注意。
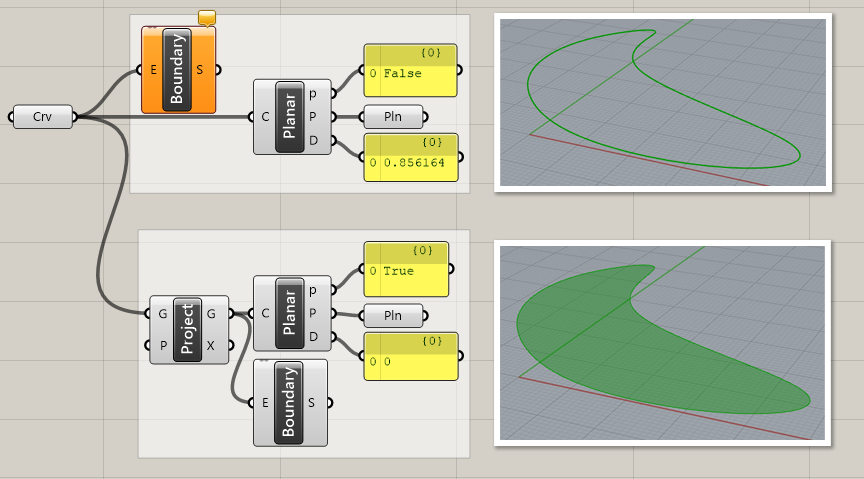
Planar*
B


Curve>Analysis
曲線(Curve)を入力し、平面上にあるかどうか(Planar)をTrue・Falseで判別する。またその平面(Plane)、偏差(Deviation)も出力する。
詳細1:カーブを入力すると、上のP端子からは平面上にあるかをTrue/Falseで出力する。2番目のP端子からはPlane、D端子からは平面との偏差を出力する。下図は平面上にない僅かに歪みのあるカーブからBoundaryが作成できない場合にPlanarで確認、Projectを用いて平面上に投影して再度Boundaryでサーフェス化した例。
Curvature*
B
Curve>Analysis
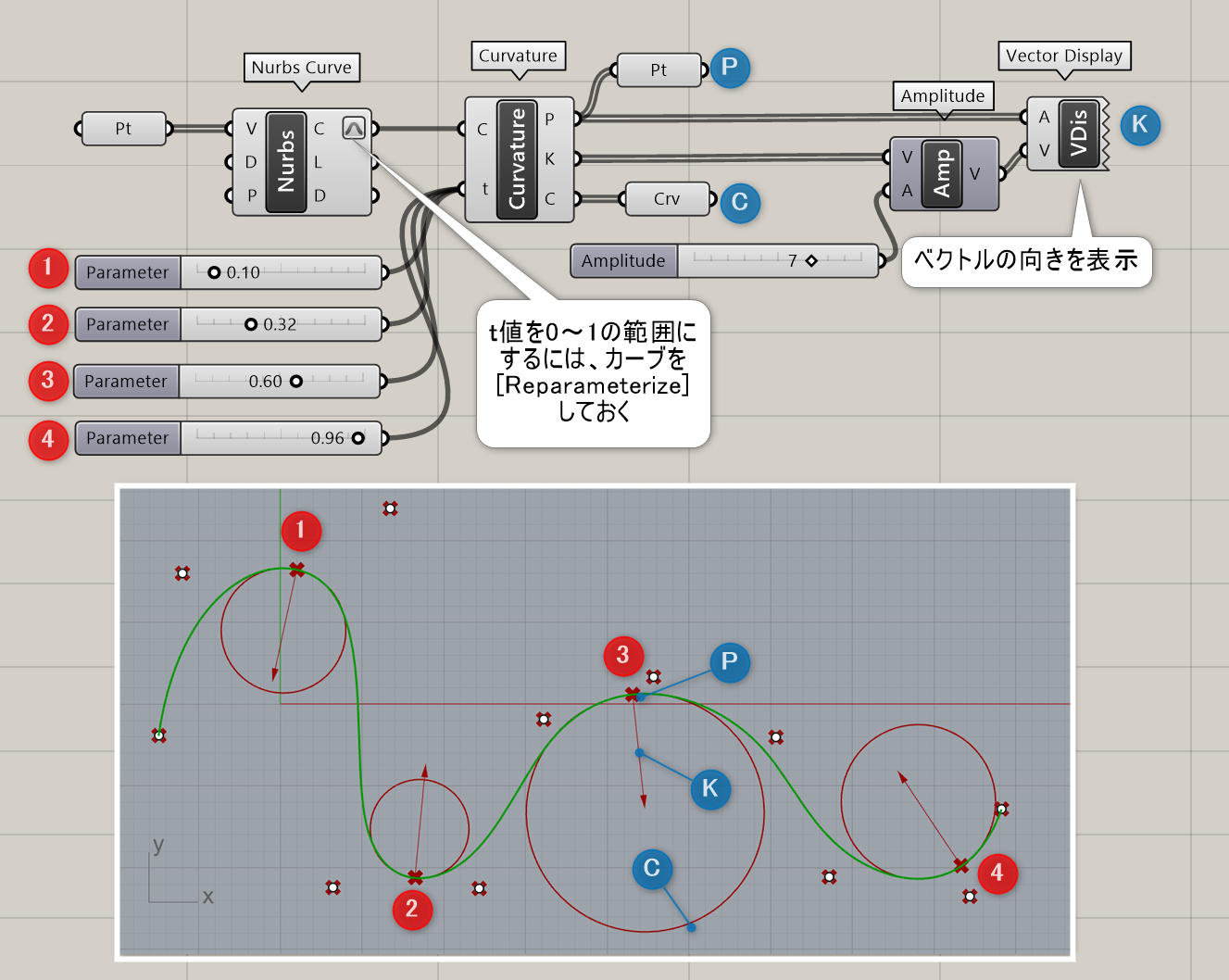
曲線(Curve)とtパラメータ値を入力し、該当箇所の点(Point)、垂線ベクトル(K)、曲率の値に応じた円を作成する。
詳細1:曲線(Curve)とtパラメータ値を入力し、該当箇所の点(P)、垂線ベクトル(K)、曲率の値に応じた円(C)を作成する。図は、4点のtパラメータにおいてそれぞれを出力したもの。
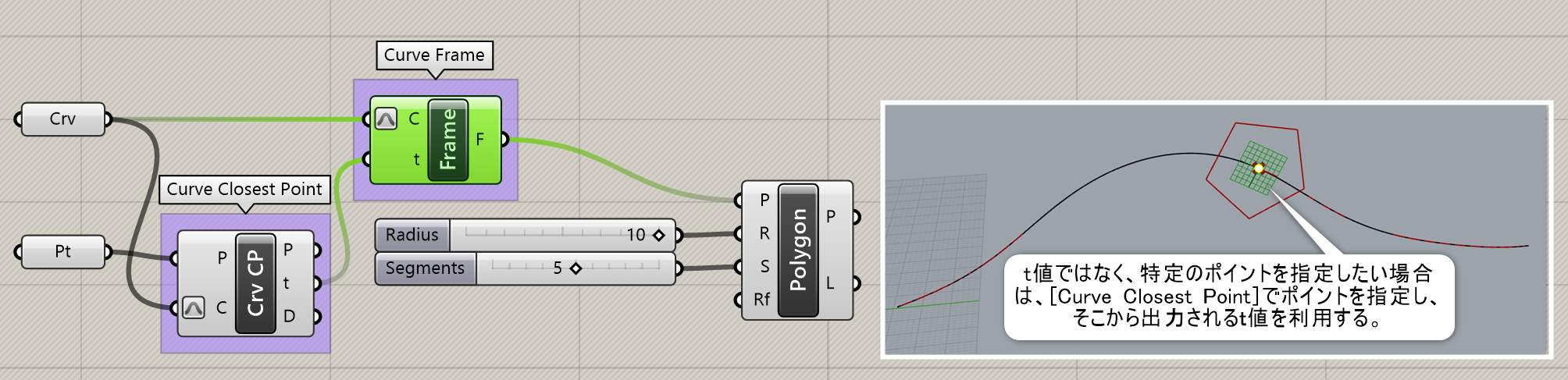
Curve Frame*
B

Curve>Analysis
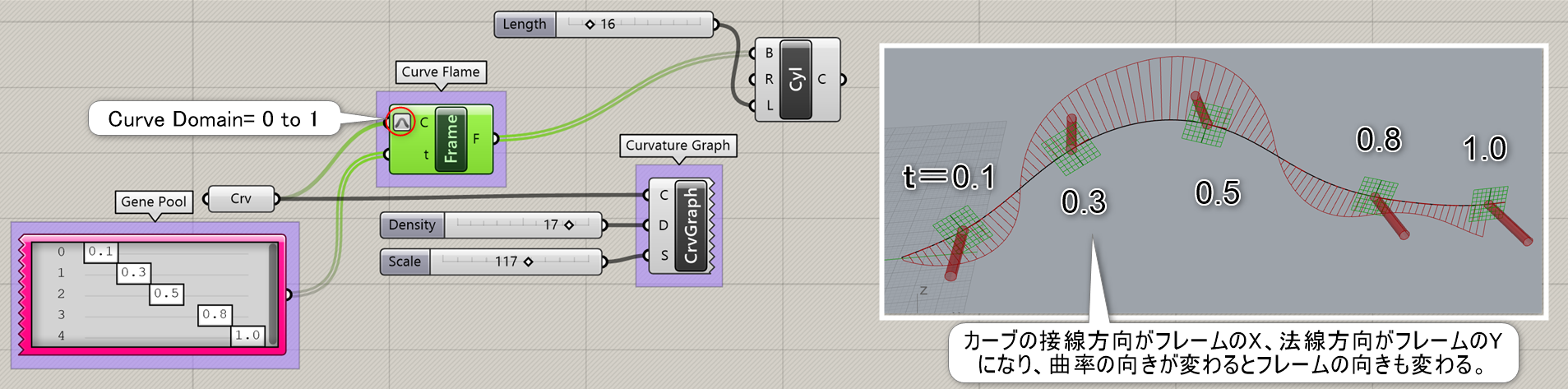
曲線(Curve)とtパラメータを入力し、曲線の進行方向に沿った平面(Plane)を出力する。平面は進行方向がX軸となる。
詳細1:カーブ上の指定したパラメーターtにおいて、接線に沿った作業平面を取得する。t値は複数入力する事ができる。フレームの向きが反転する事があるが、これは曲率が反対側へ変化すると、フレームの向きも変化するためである。向きを変化させたくない場合には、[Perp Frame]を利用してベクトルの向きを変更するなどにて対応できる場合もある。(Perp Frame参照)
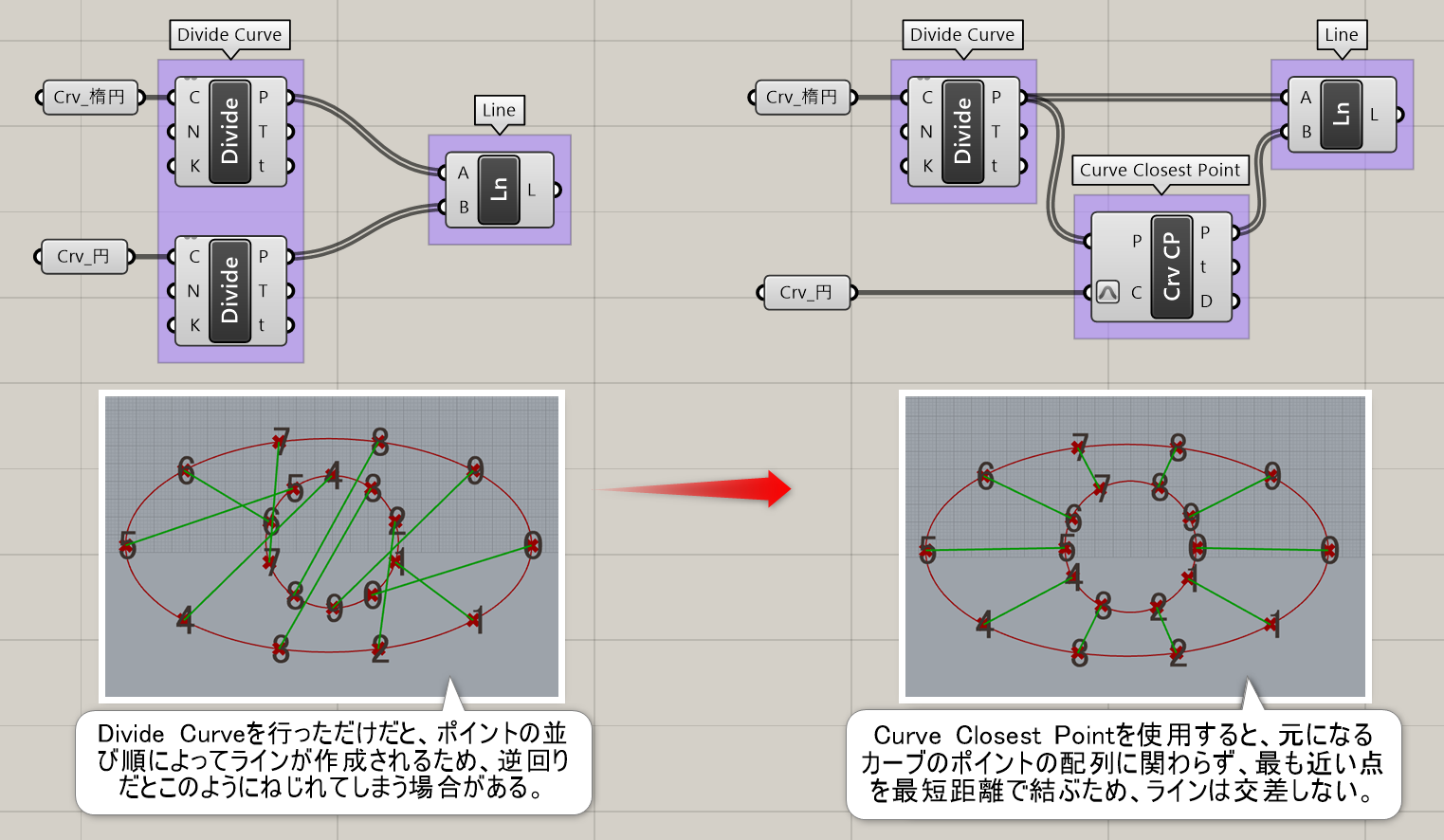
詳細2:カーブ上の平面取得位置をt値ではなく特定のポイントで指定したい場合に、[Curve Closest Point]を利用した例。
Derivatives
C

Curve>Analysis
曲線(Curve)とtパラメータ値を入力し、該当箇所の点(Point)、1からは接線ベクトルを出力する。オプションで+マークで端子を増やすことで、2からは加速度(1を微分した値)・・のように出力を増やすことが可能。
Evaluate Curve*
B
Curve>Analysis
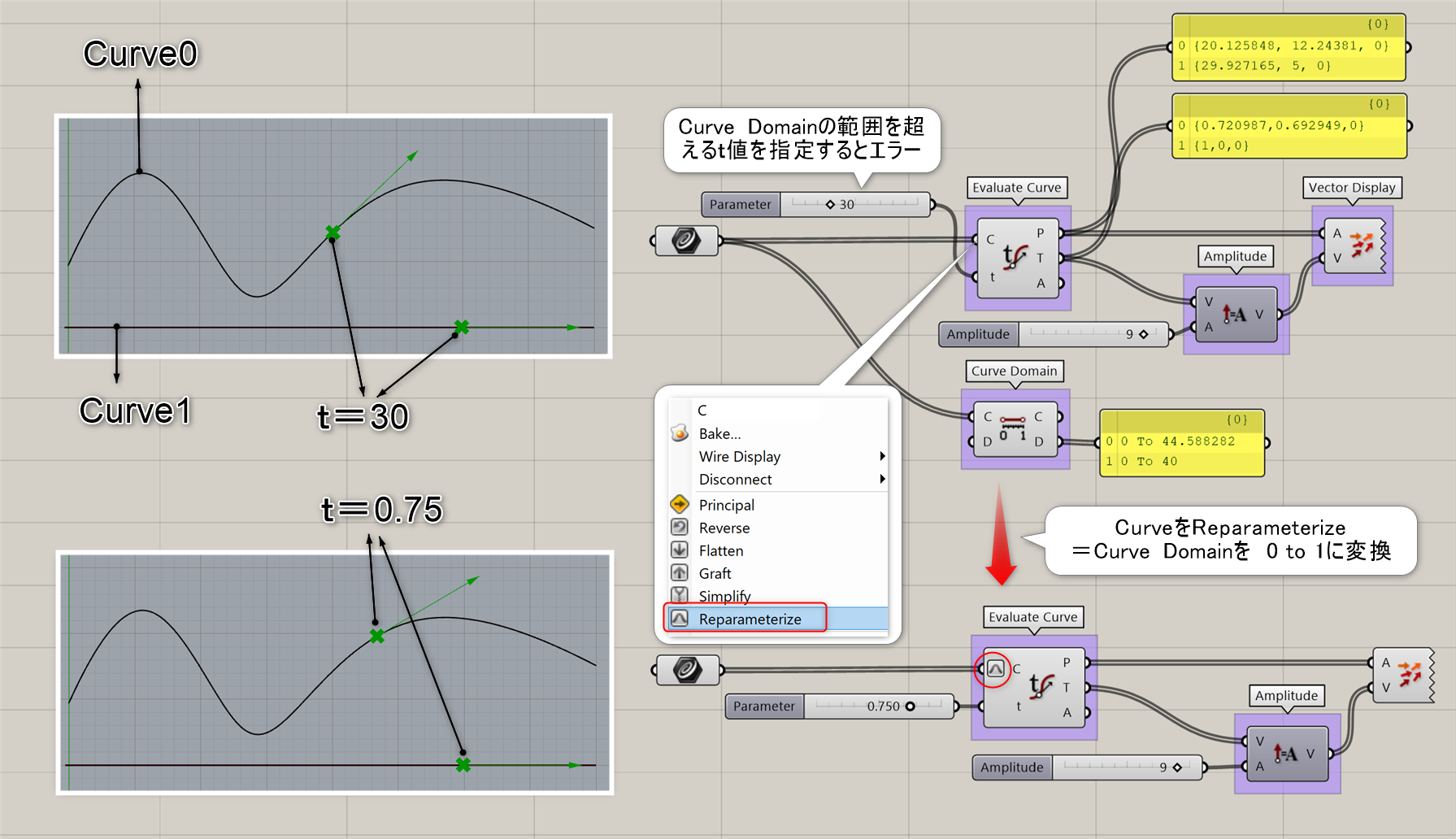
曲線(Curve)とtパラメータ値を入力し、該当箇所の点(Point)、接線ベクトル(Tangent)、曲線と接線の角度(Angle)を出力する。 t値はパラメータなので、曲線の長さの比率ではないことに注意。tパラメータに関しては、こちらのページを参照。
詳細1:指定したパラメータtによって、カーブ上のポイントや接線ベクトルの値を求める。カーブ全体のドメインは[Domain]や[Curve Domain]コンポーネントで測定でき、[0 to 40 ]のような数値で表されるが、これはカーブの長さとは無関係である。
カーブのドメインを[0 to 1]に再定義する事を[Reparameterize]と呼ぶ。出力Pからはパラメータの曲線上の位置座標を、出力Tからは接線ベクトルを出力する。
詳細2:出力Aはカーブに不連続点がある場合に利用する。端点、及び連続している部分のAngleは0になるが、[Discontinuity]で検出した不連続な部分では、接線ベクトルとの差の角度が表示される。
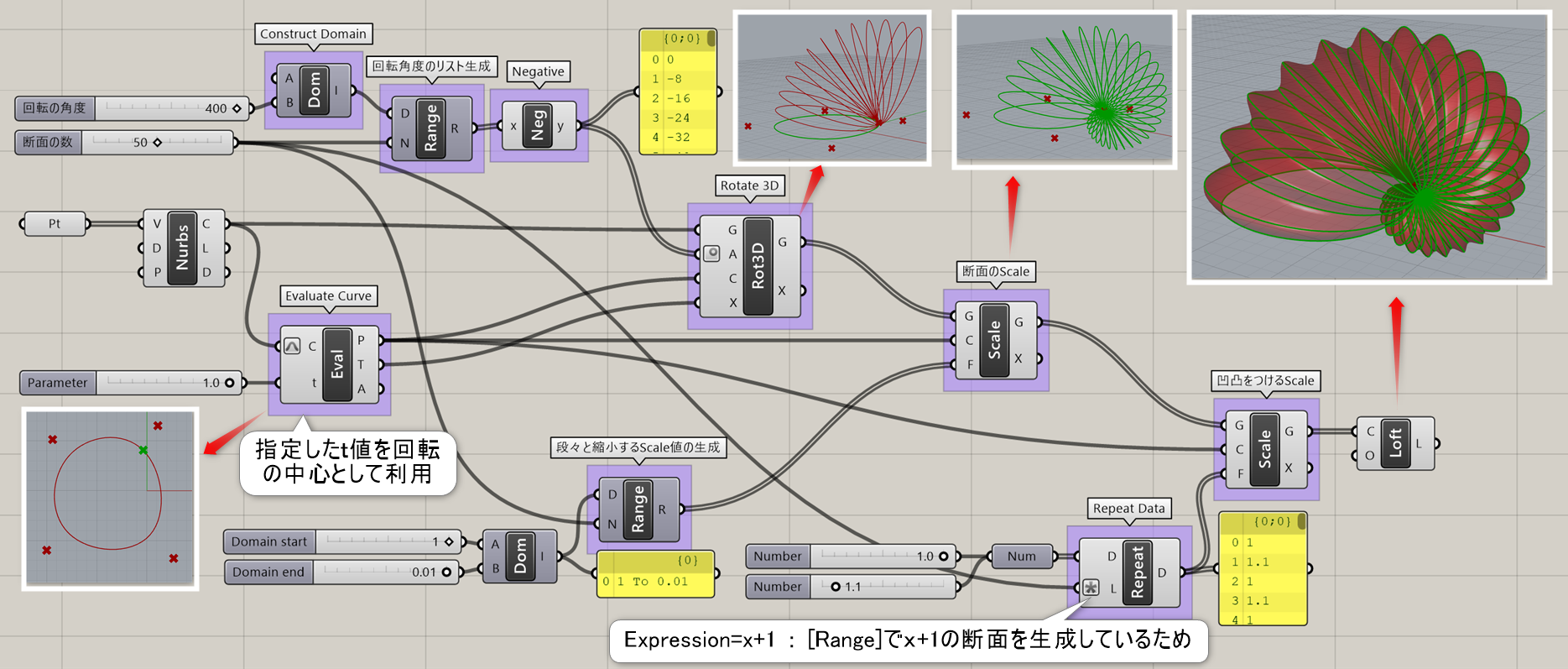
詳細3:[Evaluate Curve]で指定したt値を、回転の中心として使用した例。
Horizontal Frame*
B

Curve>Analysis
曲線(Curve)とtパラメータ値を入力し、曲線の進行方向に沿いつつワールドXY座標に平行な平面(Plane)を出力する。
Tips集の詳細ページ https://www.applicraft.com/tips/rhinoceros/gh_horizontalframe/
詳細1:カーブ上の指定したパラメーターtにおいて、XY平面に水平な作業平面を取得する。
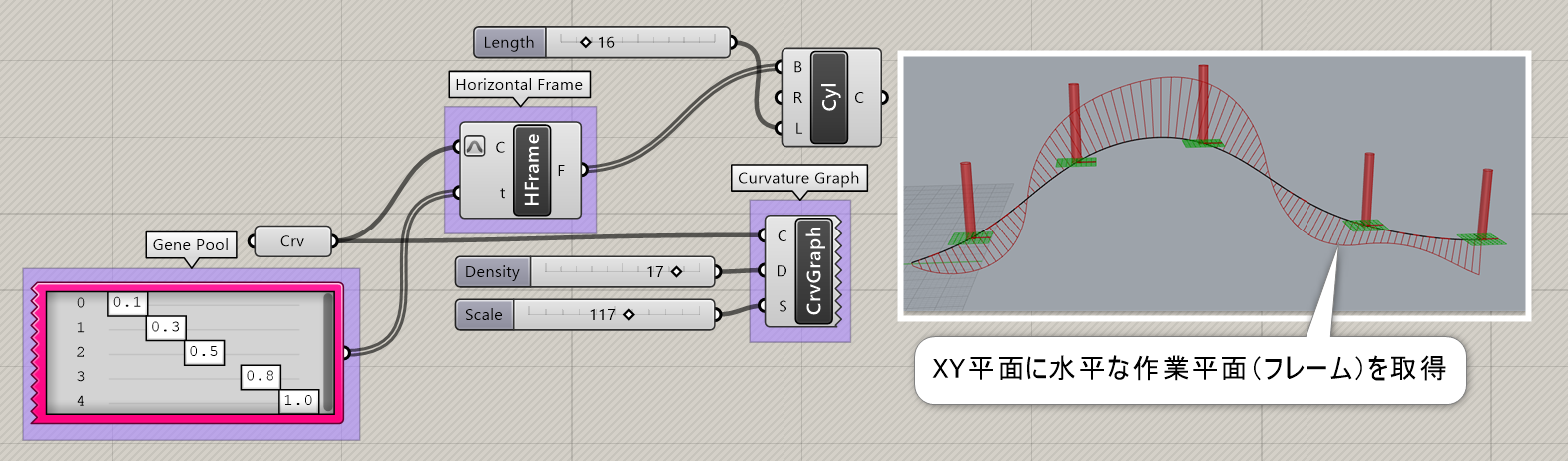
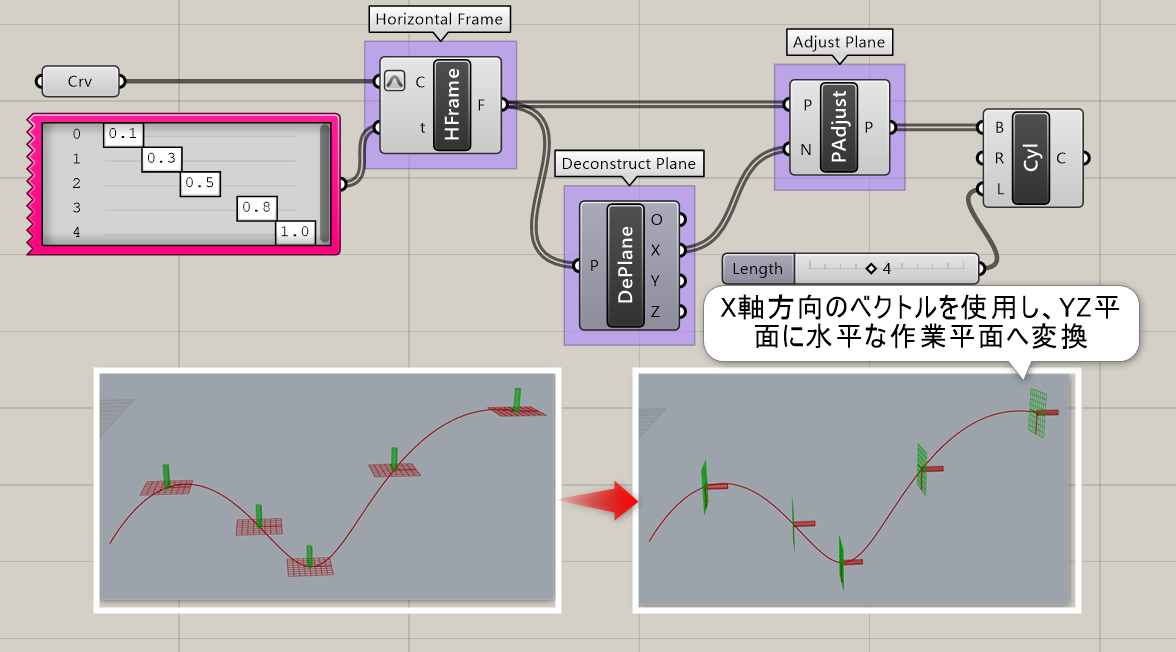
詳細2:XY平面に水平なだけでなく、[Deconstruct Plane]と[Adjust Plane]を使用すればYZ平面やXZ平面に水平な作業平面も取得可能。
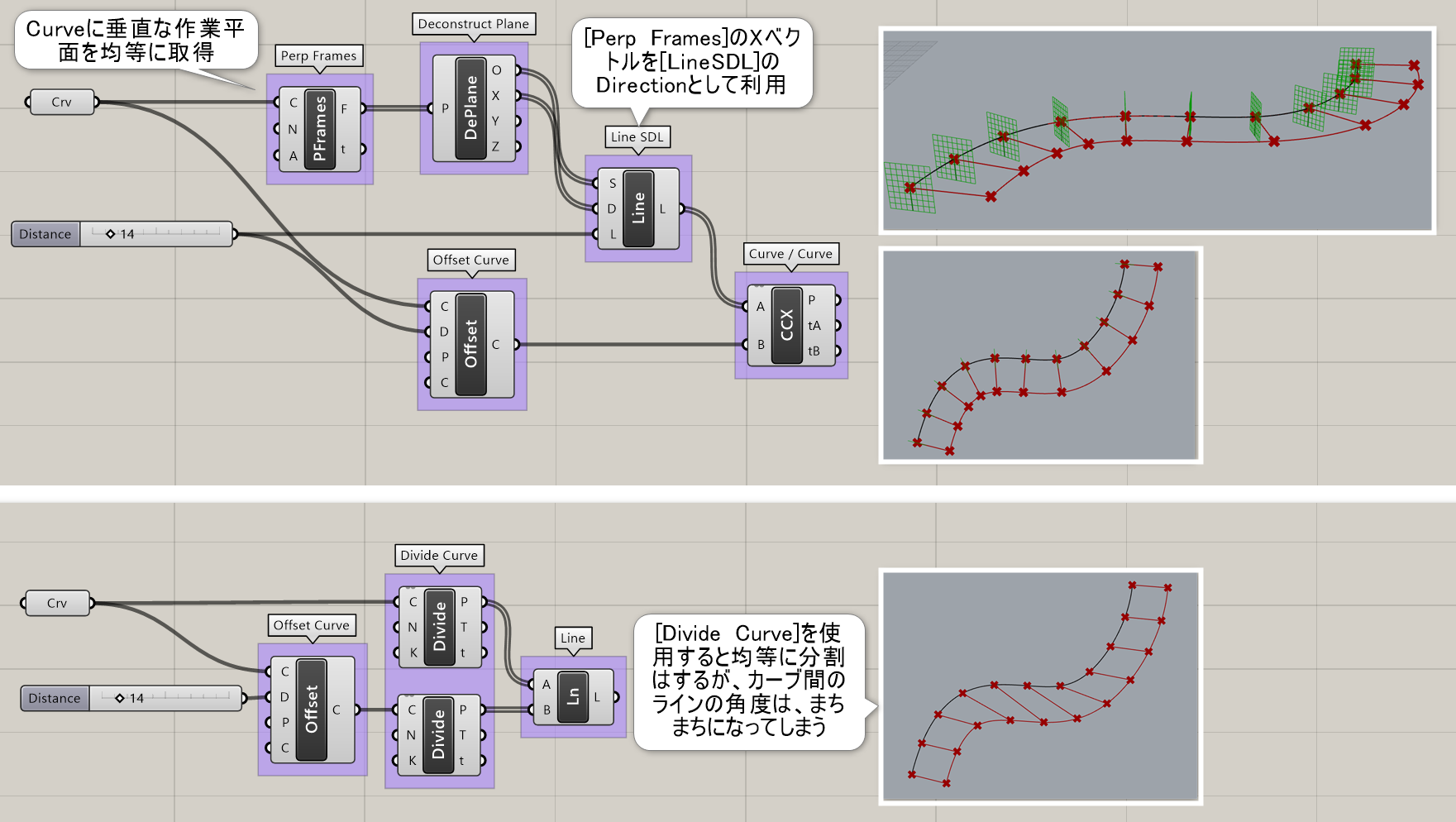
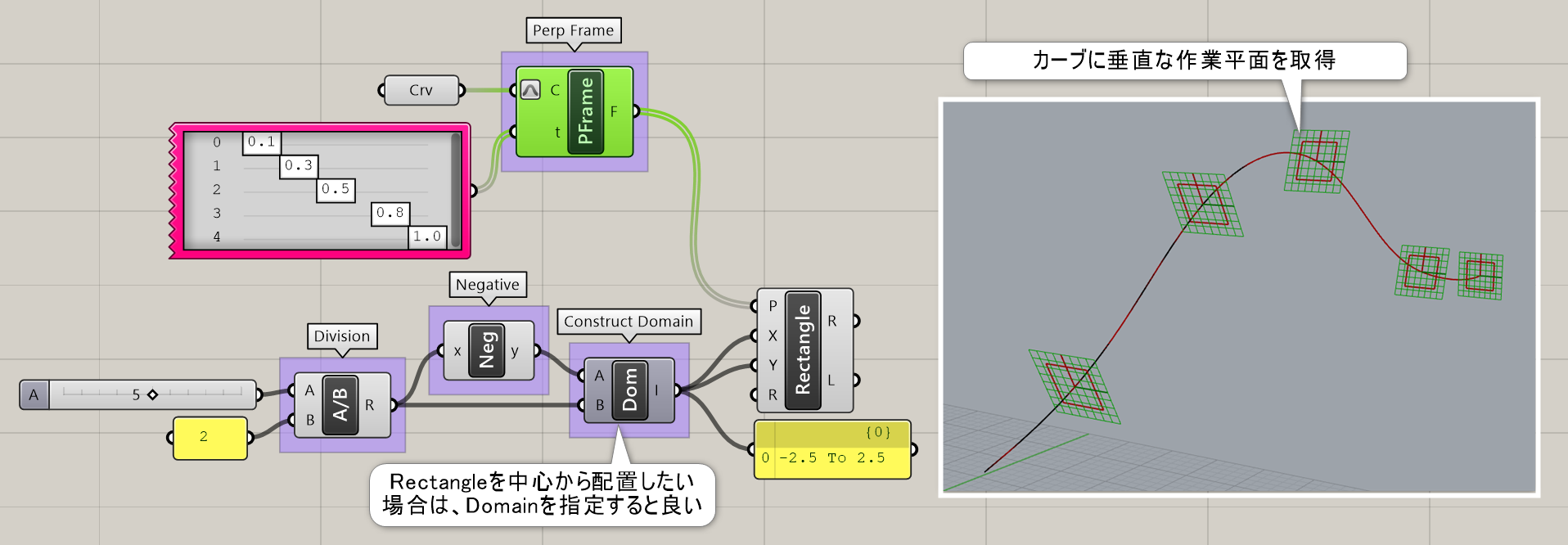
Perp Frame*
B


Curve>Analysis
曲線(Curve)とtパラメータ値を入力し、曲線の進行方向と垂直な平面(Plane)を出力する。
詳細1:カーブ上の指定したパラメーターtにおいて、カーブに垂直な作業平面を取得する。図は、[Rectangle]を中心から配置するために、ドメインを使用した例。(デフォルトではRectangleの左下角が作業平面の原点になる)
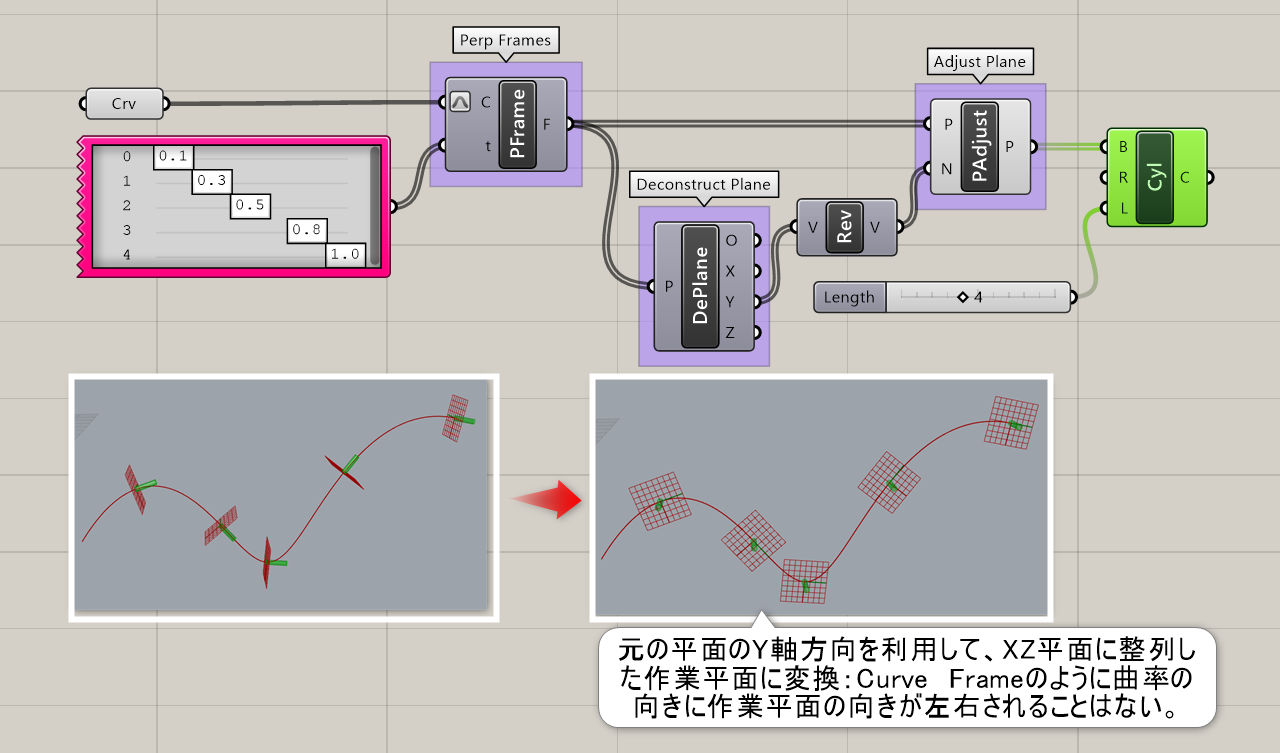
詳細2:[Deconstruct Plane]と[Adjust Plane]を使用して、作業平面の向きを変換した例。
Point On Curve*
A
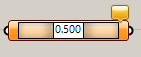
Curve>Analysis
曲線(Curve)を入力し、値を指定して点(Point)を出力する。このコンポーネントでは、値は曲線の実際の長さの比率。
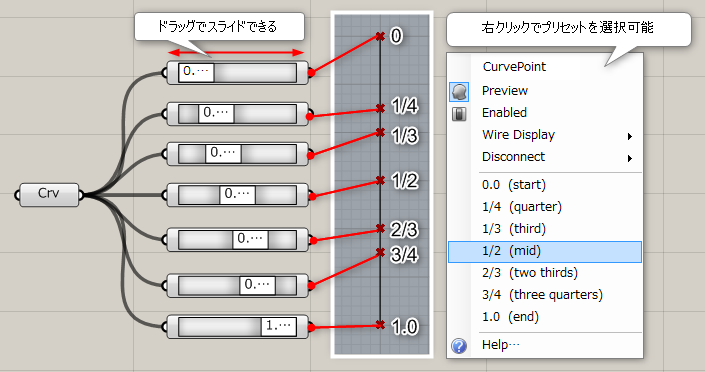
詳細1:カーブ上の任意の点を出力する。右クリックによるコンテキストメニューから、0,1/4,1/3,1/2,2/3,2/4,1などのプリセットが選択でき、中点などを取得するにも便利である。
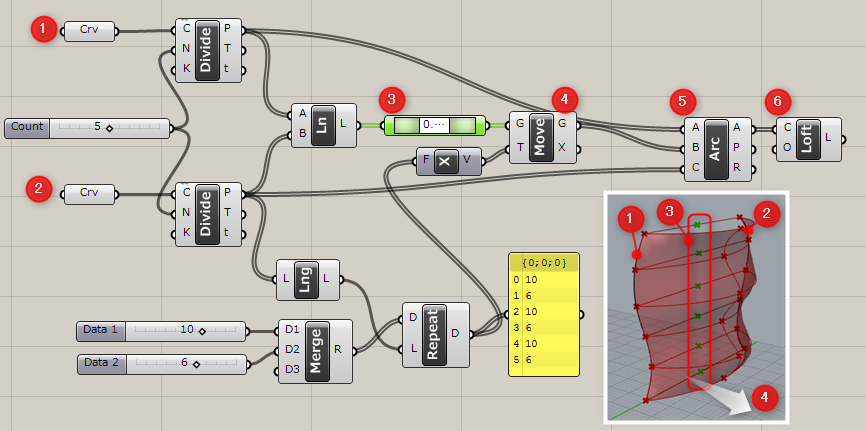
詳細2:[Point On Curve]コンポーネントで中点を取得した例。
①と②のCurveを[Divide]コンポーネントで分割し,その分割点間にラインを作成
③[Point On Curve]コンポーネントで中点を出力
④[Move]コンポーネントを利用して[X]方向に移動。その際[Repeat data]コンポーネントを使用してポイントを波状に移動
⑤[Arc3Pt]で①~③のポイントを円孤でつなぎ
⑥[Loft]でサーフェスを生成
Torsion
C

Curve>Analysis
曲線(Curve)とtパラメータ値を入力し、該当箇所の点(Point)とねじれ率(Torison)を出力する。
Curve Domain
C
Curve>Analysis
曲線(Curve)とドメインとなる値を入力し、ドメイン値を変えた曲線(Curve)を出力する。0 to 1 をドメインとして入力すると、Reparametrizeオプションと同様の効果。
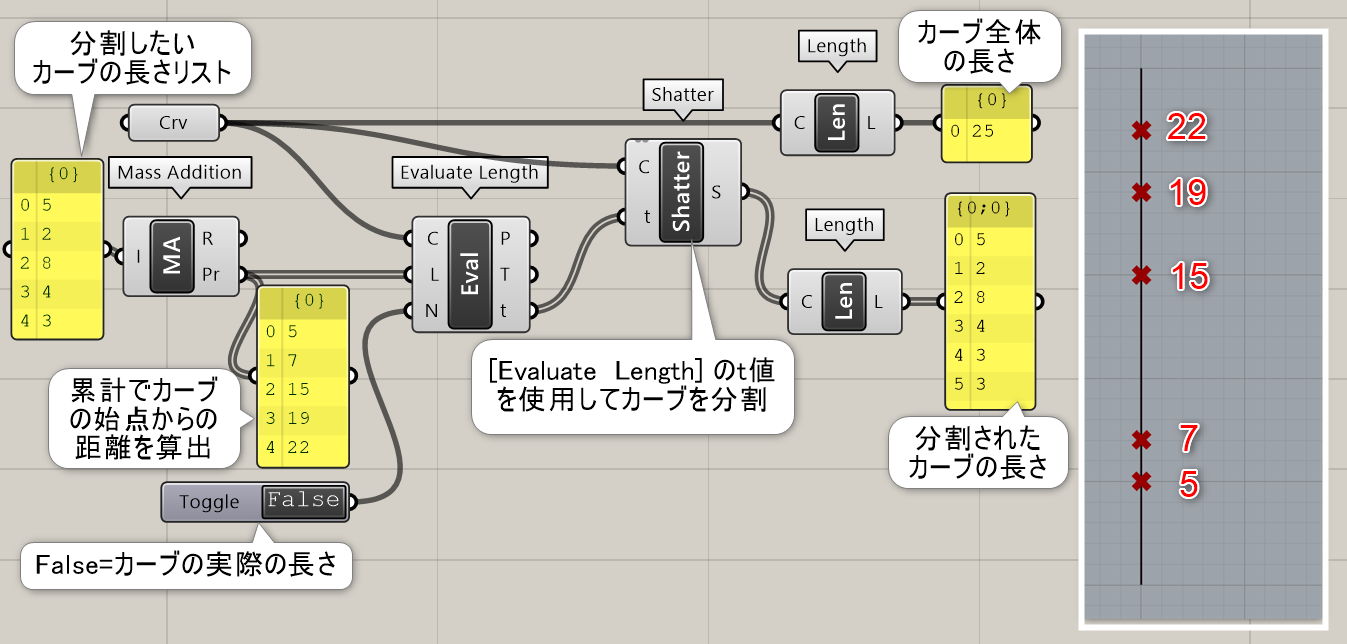
Evaluate Length*
B

Curve>Analysis
曲線(Curve)と長さ(Length)を入力し、曲線上の該当箇所の点(Point)、接線ベクトル(Tangents)とtパラメータ値を出力する。NormalizedオプションはFalseだと実際の曲線長さ、Trueだと0から1までのパラメータ値で長さを扱う。
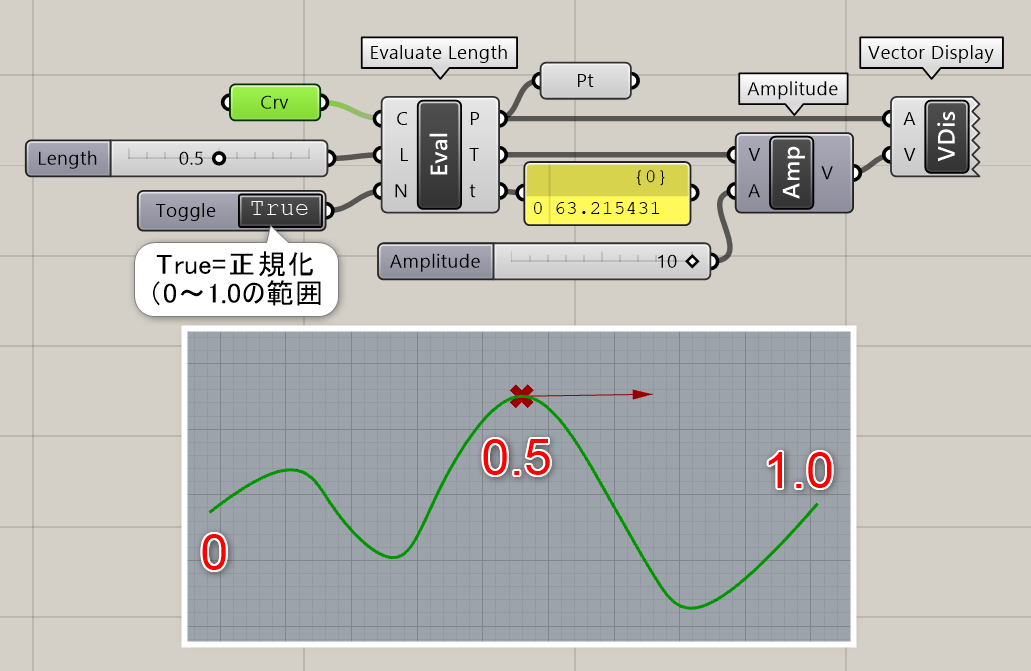
詳細1:曲線(Curve)と長さ(Length)を入力し、曲線上の該当箇所の点(Point)、接線ベクトル(Tangents)とtパラメータ値を出力する。Normalizedオプションは”False”だと実際の曲線長さ、”True”だと0から1までのパラメータ値で長さを扱う。図は、”True”で正規化し、0.5の長さ(中点)におけるベクトルを表示した例。
詳細2:[Evaluate Length]の長さは始点からの距離なので、[Mass Addition]のPr(累計)出力を利用して、異なる長さで線分を分割した例。
Length*
A

Curve>Analysis
入力した曲線(Curve)の長さ(Length)を出力する。
Length Domain
C

Curve>Analysis
曲線(Curve)と範囲となるドメイン(Domain)を入力し、その長さ(Length)を出力する。
Length Paramater
C

Curve>Analysis
Segment Lengths
C
Curve>Analysis
入力したポリカーブ(曲線)の最も短い曲線と長い曲線の長さ(Length)と範囲(Domain)の値をそれぞれ出力する。
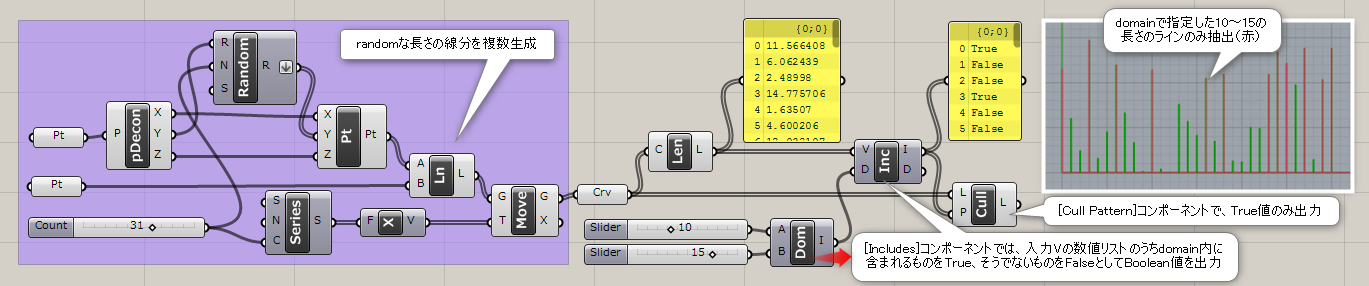
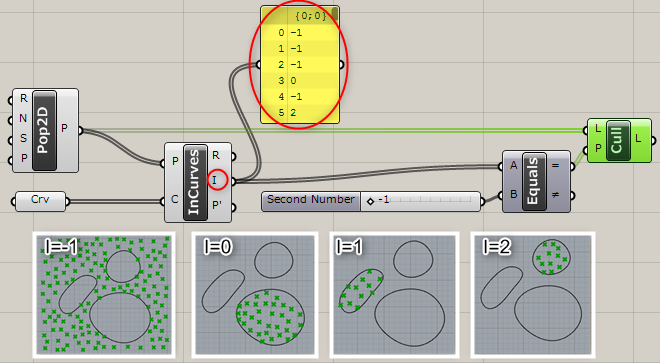
Point In Curve*
A
Curve>Analysis
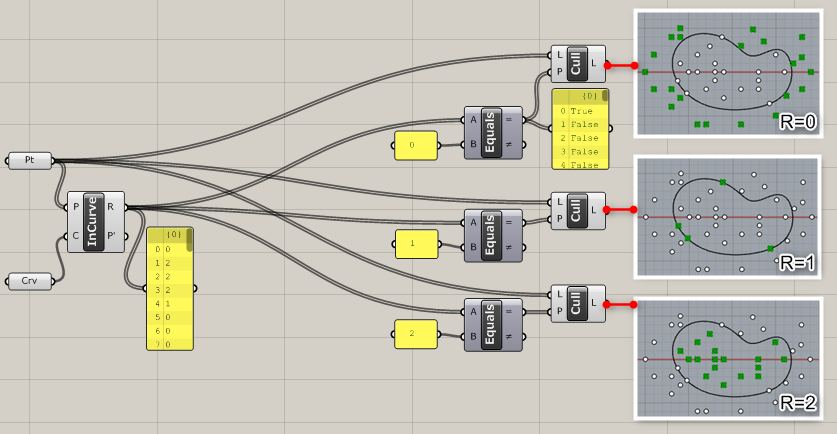
閉じた一本の曲線(Curve)と複数の点(Points)を入力し、内外判定を行う。0が外側、1が曲線上、2が内側。
詳細1:カーブと、点群の内外判定を行う。
出力Rが”0”の場合は=外側、”1″の場合=カーブ上、”2″の場合=内側と判定。図は、これらの数値を使用して、[Equality]コンポーネントと[Cull Pattern]コンポーネントでそれぞれのポイントを振り分けた例。
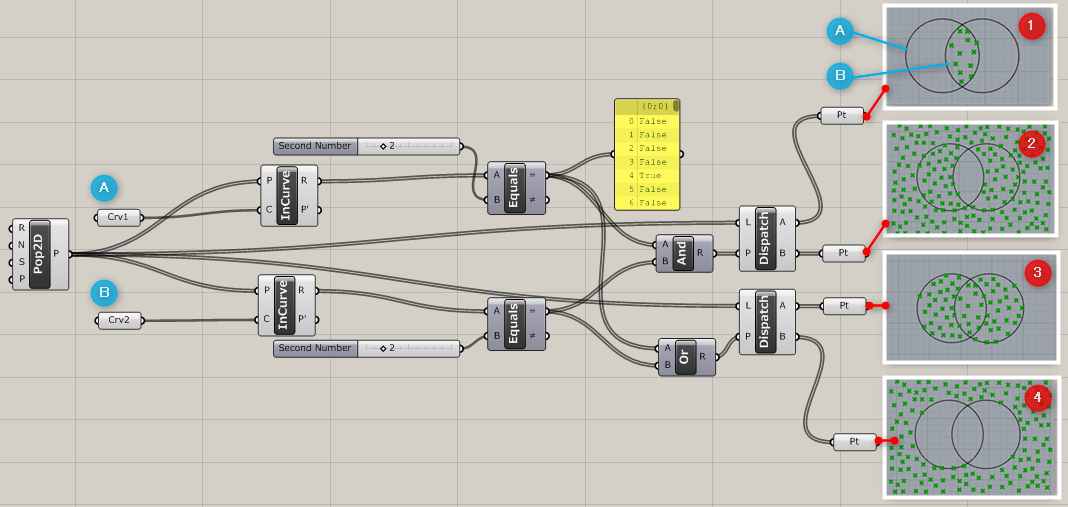
詳細2:[Gate And]コンポーネントと[Gate Or]コンポーネントを使用して、2つの円の条件分けを行った例。
①AかつB
②Aでもなく、かつBでもない
③AまたはB
④Aでもない、またはBでもない
Point In Curves*
A

Curve>Analysis
閉じた複数の曲線(Curve)と複数の点(Points)を入力し、内外判定を行う。0が外側、1が曲線上、2が内側。また何番目の曲線に含まれるかをIndexから出力する。
詳細1:複数カーブと、点群の内外判定を行う。詳細は[Point In Curve]に準ずる。
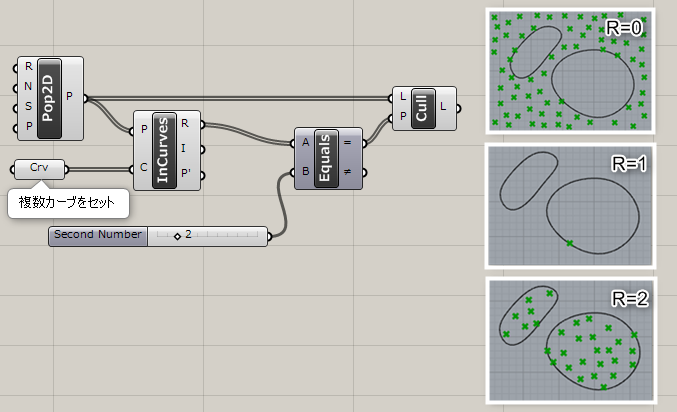
詳細2:[Point In Curves]のみにある出力Iからは、インデックス値が出力される。”-1″はカーブの外側の点群を選択。”0″から順に選択したカーブごとにインデックス値が与えられ、それを使用してカーブ内部の点を切り替え可能。
Division
Contour(ex)
C
Curve>Division
曲線(Curve)、開始する平面(Plane)を入力し、点(Contours)を作成する。また該当となる点のtパラメータ値も出力する。距離の指定は、元の平面をオフセットする値(Offsets)か、平面同士の間隔(Distances)かどちらかで指定する。
Curve Contour
C
Curve>Division
曲線(Curve)、始点(Point)、方向ベクトル(Direction)、間隔(Distance)を入力し、等間隔になるように点(Contours)を作成する。また該当となる点のtパラメータ値も出力する。Rhino7以前のContourコンポーネント。
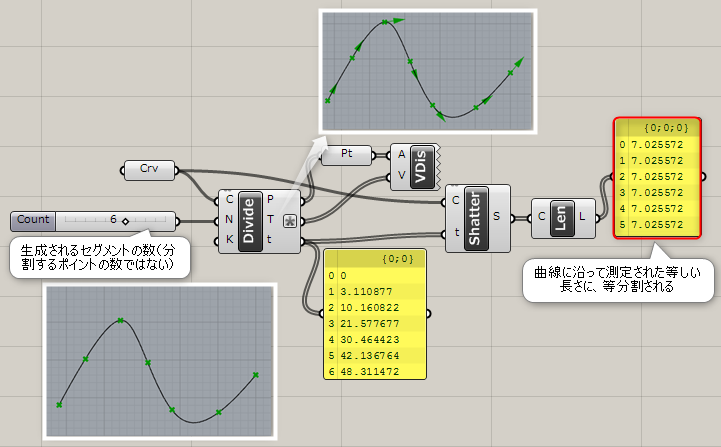
Divide Curve*
A


Curve>Division
曲線(Curve)と分割数(Count)を入力し、曲線を等間隔にする箇所に点(Points)を作成する。また作成された点における接線ベクトル(Tangents)とtパラメータ値も出力する。
詳細1:カーブを入力Nで指定した数で複数のセグメント(曲線に沿って測定)に分割する。出力Pからは分割したポイントデータ、出力Tからはベクトルデータ、出力tからは分割ポイントのtパラメータが出力される。
図は、出力されたtパラメータを[Shatter]コンポーネントに接続し、分割された各セグメントの長さを確認した例。
Dash Pattern
C


Curve>Division
曲線(Curve)と複数の長さ(Pattern)を入力し、長さ毎に曲線を分割する。分割された曲線は互い違いになる様に、一つ置きにDashesとGapsから出力される。
Divide Distance*
B
Curve>Division
曲線(Curve)と距離(Distance)を入力し、指定点間の距離毎に曲線上の点(Points)を作成する。また作成された点における接線ベクトル(Tangents)とtパラメータ値も出力する。曲線の長さではなく、点と点の距離なので注意。
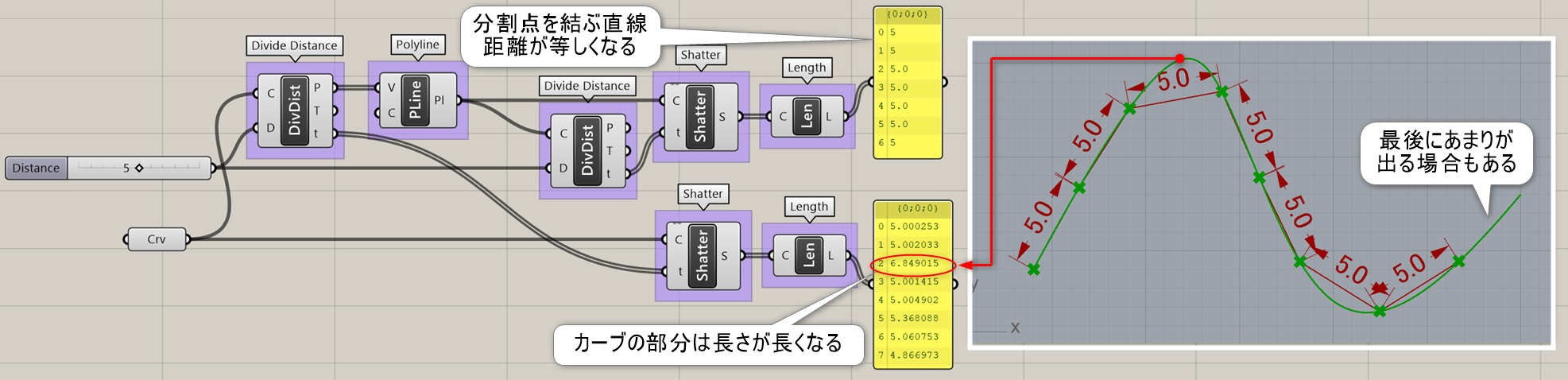
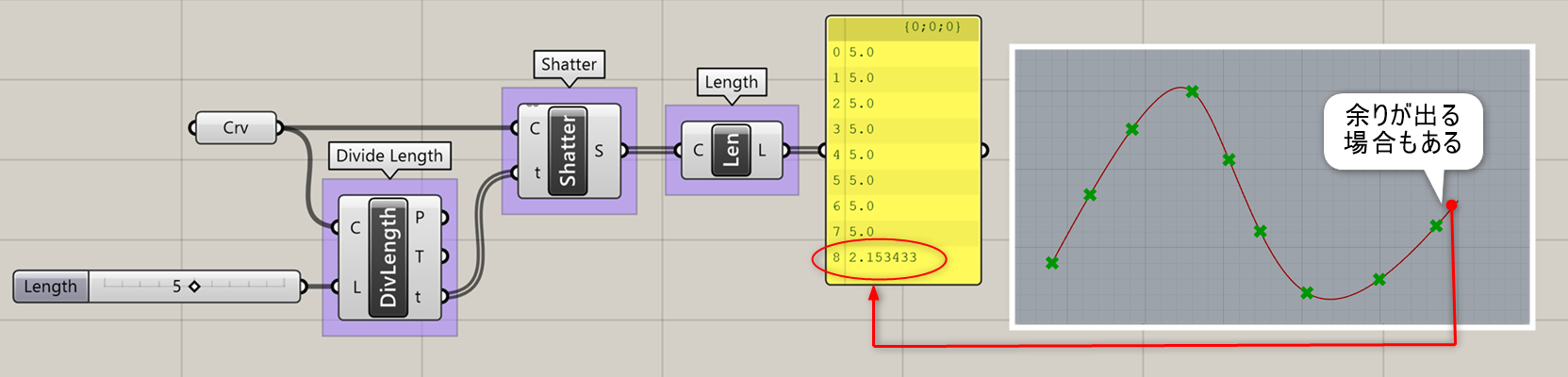
Divide Length*
B
Curve>Division
曲線(Curve)と長さ(Length)を入力し、指定曲線の長さ毎に曲線上の点(Points)を作成する。また作成された点における接線ベクトル(Tangents)とtパラメータ値も出力する。
詳細1:カーブを指定した長さのセグメントに分割。セグメントはすべて曲線に沿って測定され、最後のセグメントは余りの長さとなる場合もある。
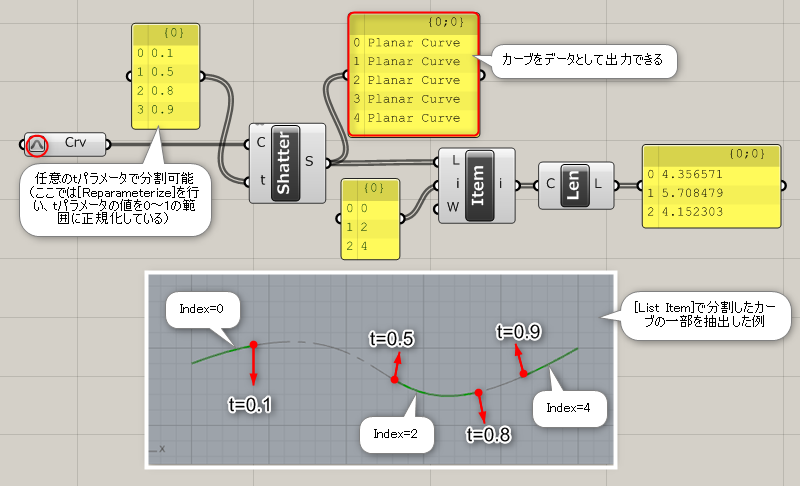
Shatter*
A


Curve>Division
曲線(Curve)とtパラメータ値を入力し、該当箇所で分割した曲線(Segments)を出力する。
詳細1:[Divide Curve]コンポーネントや[Divide length]コンポーネントのように数や長さで等分割するのではなく、カーブ上の任意のt値で分割し、そのカーブデータを出力できる。このt値は、Divide系のコンポーネントからも出力可能。(Divide Curve参照)
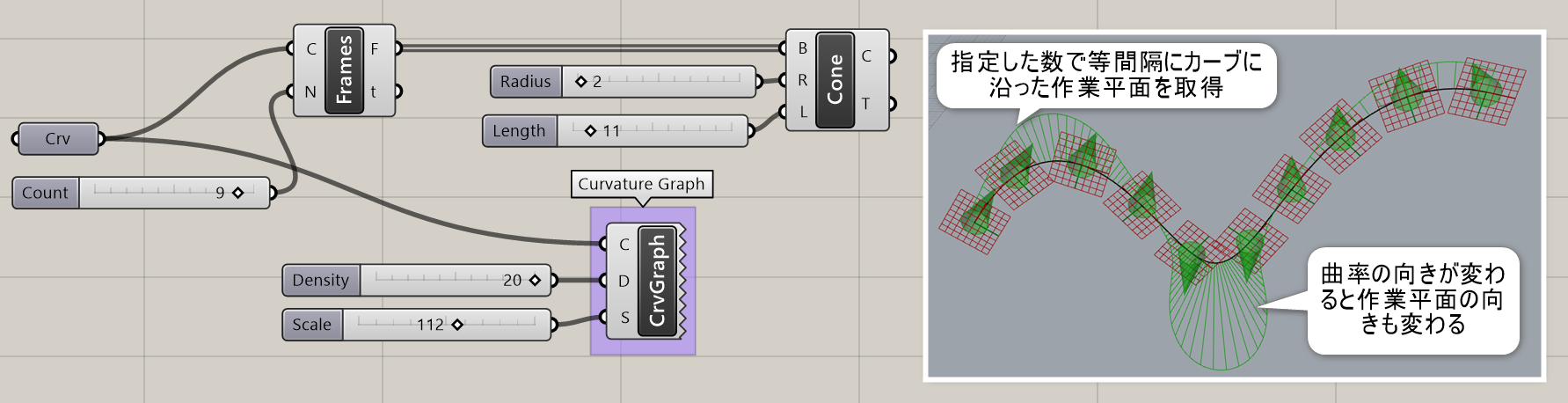
Curve Frames*
B


Curve>Division
曲線(Curve)と作成数(Count)を入力し、曲線を等分割する箇所に平面(Frames)を作成する。平面は、曲線の進行方向をX軸にする形で作成される。
詳細1:カーブ上に、接線方向に沿った作業平面を、指定した数で等間隔に配置する。[Curve Frame]と同様に、曲率の向きが変わると作業平面の向きも変化する。[Perp Frame(s)] を使用する事で向きを揃える事は可能。(PerpFrame参照)
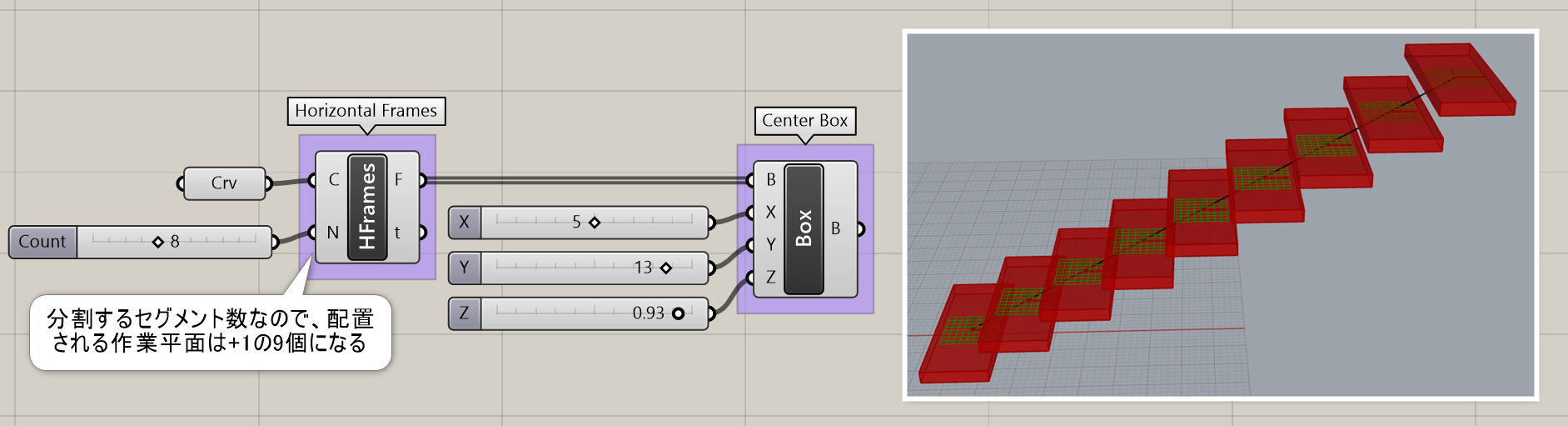
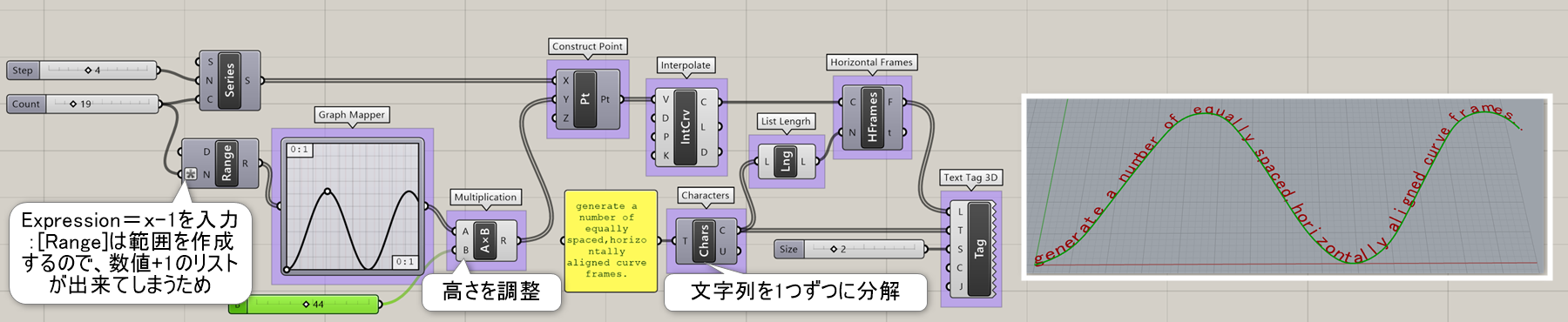
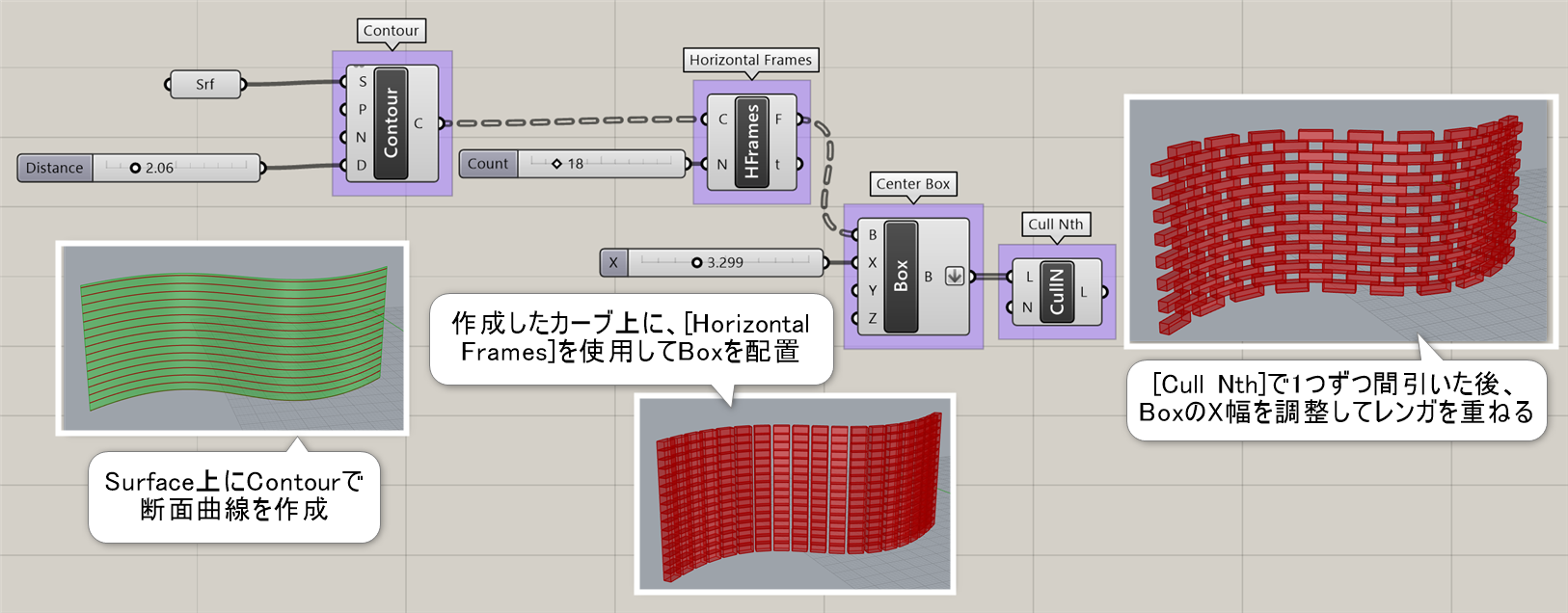
Horizontal Frames*
B
Curve>Division
曲線(Curve)と作成数(Count)を入力し、曲線を等分割する箇所に平面(Frames)を作成する。平面は、曲線の進行方向をX軸にしつつ、ワールドXY平面に平行な形で作成される。
Tips集の詳細ページ https://www.applicraft.com/tips/rhinoceros/gh_horizontalframe/
Perp Frames*
B
Curve>Division
曲線(Curve)と作成数(Count)を入力し、曲線を等分割する箇所に平面(Frames)を作成する。平面は、曲線の進行方向に垂直になる形で作成される。オプションで平面の向きを揃える(Align)をTrue・Falseで指定できる。
Tips集の詳細ページ
https://www.applicraft.com/tips/rhinoceros/perpframes/
Primitive
Fit Line
C

Curve>Primitive
複数の点(Points)を入力し、入力した点にできる限り近しい直線(Line)を出力する。
Line*
B

Curve>Primitive
点A(Point)と点B(Point)を繋ぐ、直線(Line)を作成する。
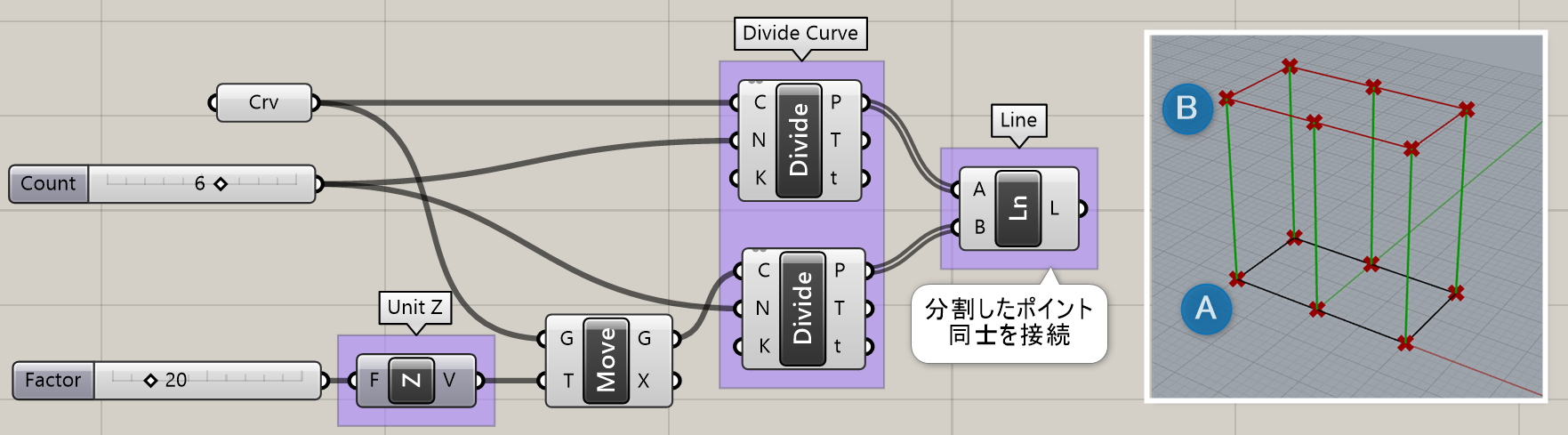
詳細1:2点から直線を作成する。図は、カーブを分割した頂点同士を[Line]で接続した例。
Line 2Plane
C

Curve>Primitive
直線(Line)を入力し、平面A、平面Bの位置まで延長・短縮する形で新しい直線を作成する。
Line 4Pt
C

Curve>Primitive
直線(Line)を入力し、点A、点Bの位置まで延長・短縮する形で新しい直線を作成する。
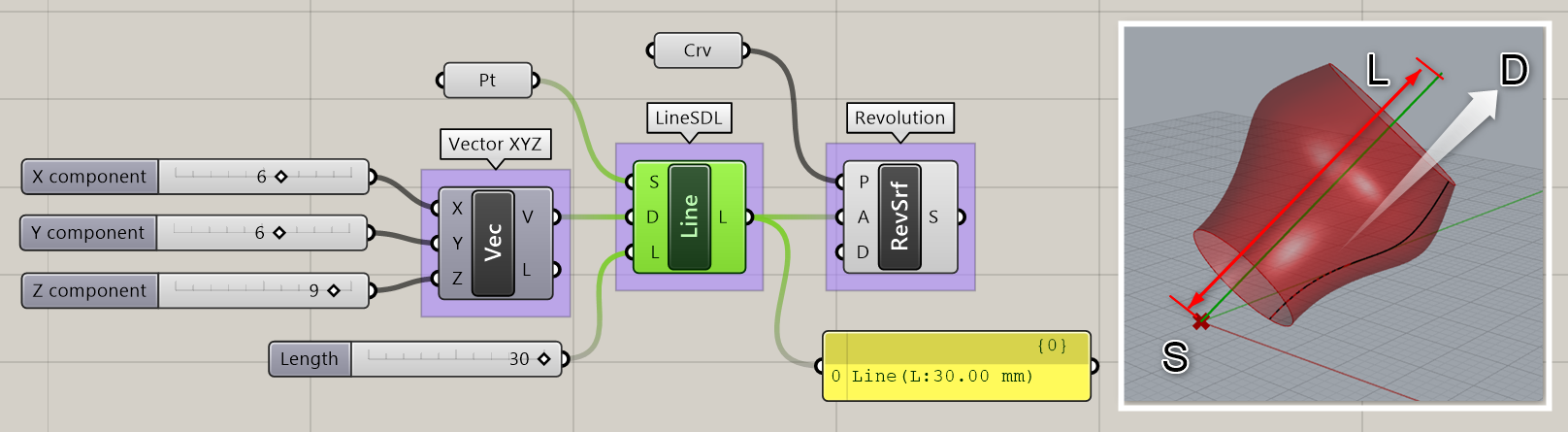
Line SDL*
B

Curve>Primitive
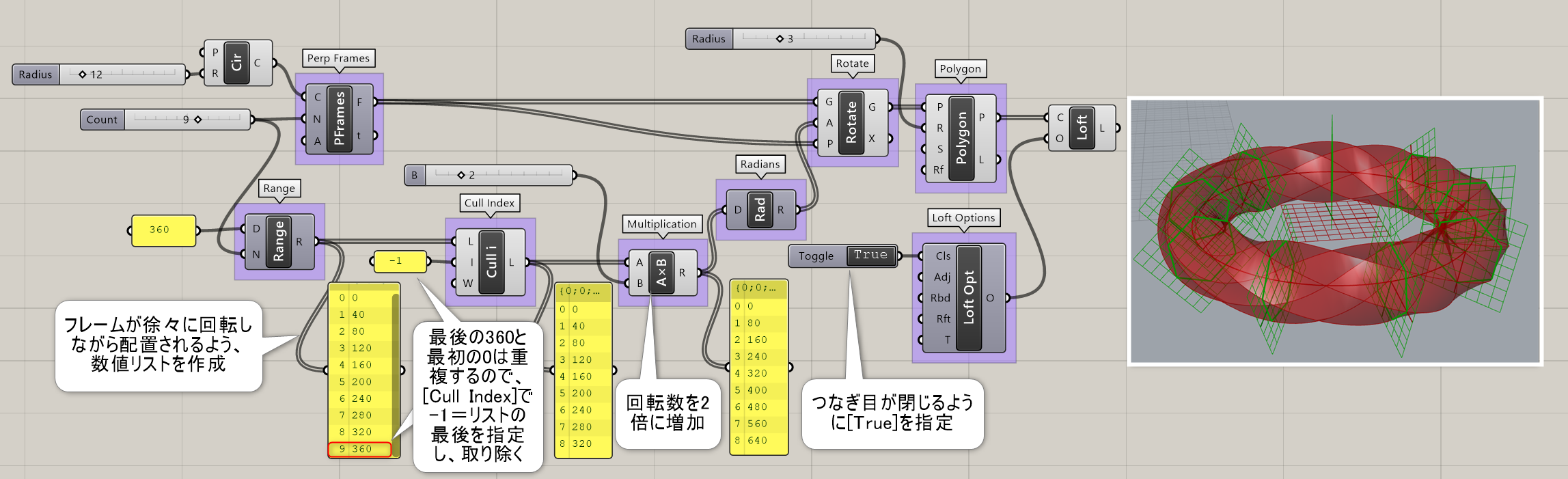
始点(Start)、方向ベクトル(Direction)、長さ(Length)を入力し、直線(Line)を作成する。
詳細1:始点(S)とベクトル(D)と長さ(L)により定義された直線を作成する。図は、LineSDLがベクトルを定義する事を利用して、[Revolution]の回転軸として[LineSDL]を使用した例。
詳細2:[LineSDL]を使用して作成したラインを[Linear Array]で配列し、[Graph Mapper]で回転角度を調整した例。
Tangent Lines
C

Curve>Primitive
点(Point)と円(Circle)を入力し、点から円に接する接線2つをそれぞれ出力する。
Tangent Lines(Ex)
C

Curve>Primitive
円A・B(Circle)を入力し、交差しない円同士を繋ぐ接線2つをそれぞれ出力する。
Tangent Lines(In)
C
Curve>Primitive
円A・B(Circle)を入力し、交差する円同士を繋ぐ接線2つをそれぞれ出力する。
Circle*
B
Curve>Primitive
平面(Plane)と半径(Radius)を入力し、平面の原点を中心とする円(Circle)を作成する。
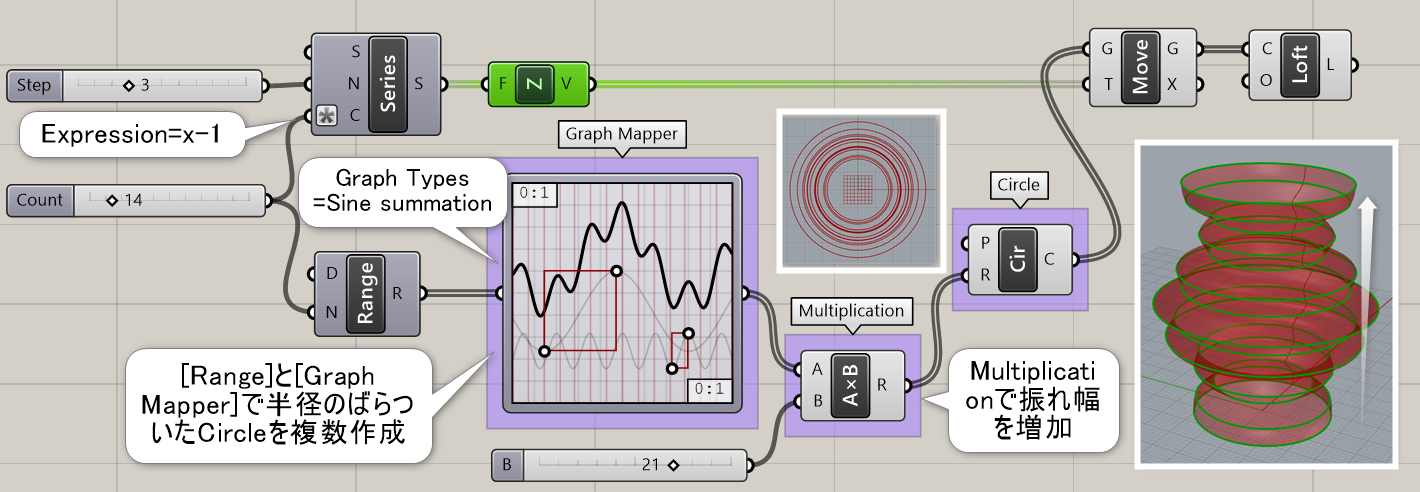
詳細1:基本平面(P)と半径(R)により定義された円を作成する。図は、半径入力に[Range]と[Graph Mapper]を利用して、半径の異なる円を複数作成し、Z方向に移動して[Loft]でサーフェスを作成した例。
Circle 3Pt
C
Curve>Primitive
点(Point)を3つそれぞれ入力し、3点を通過する円(Circle)、円ができる平面(Plane)、円の半径(Radius)を出力する。
Circle CNR
C

Curve>Primitive
中心となる点(Point)、垂直方向ベクトル(Normal)、半径(Radius)を入力し、円(Circle)を作成する。
Circle Fit
C
Curve>Primitive
複数の点(Points)を入力し、出来る限り近しい円(Circle)を作成する。その際、作成した円の半径(Radius)と偏差(Deviation)も出力する。
Circle TanTan
C
Curve>Primitive
曲線A、B(Curve)と点(Point)を入力し、曲線に接する円(Circle)を作成する。作成する円の中心座標は、点に近い位置になる。
Circle TanTanTan
C
Curve>Primitive
曲線A、B、C(Curve)と点(Point)を入力し、曲線にそれぞれ接する円(Circle)を作成する。入力点は、接する円の方向を決める為に使用する。
Ellipse*
C

Curve>Primitive
平面(Plane)と半径1,2(Radius)を入力し、だ円(Ellipse)を作成する。焦点もそれぞれF1,F2から出力される。
InCircle
C
Curve>Primitive
点(Point)を3つそれぞれ入力し、三角形に内接する円(Circle)、円ができる平面(Plane)、円の半径(Radius)を出力する。
InEllipse
C
Curve>Primitive
点(Point)を3つそれぞれ入力し、三角形に内接するだ円(Circle)、だ円ができる平面(Plane)を出力する。
Arc*
B
Curve>Primitive
平面(Plane)と半径(Radius)、範囲(Angle)を入力し、円弧(Arc)を作成する。円弧の長さ(Length)も出力する。
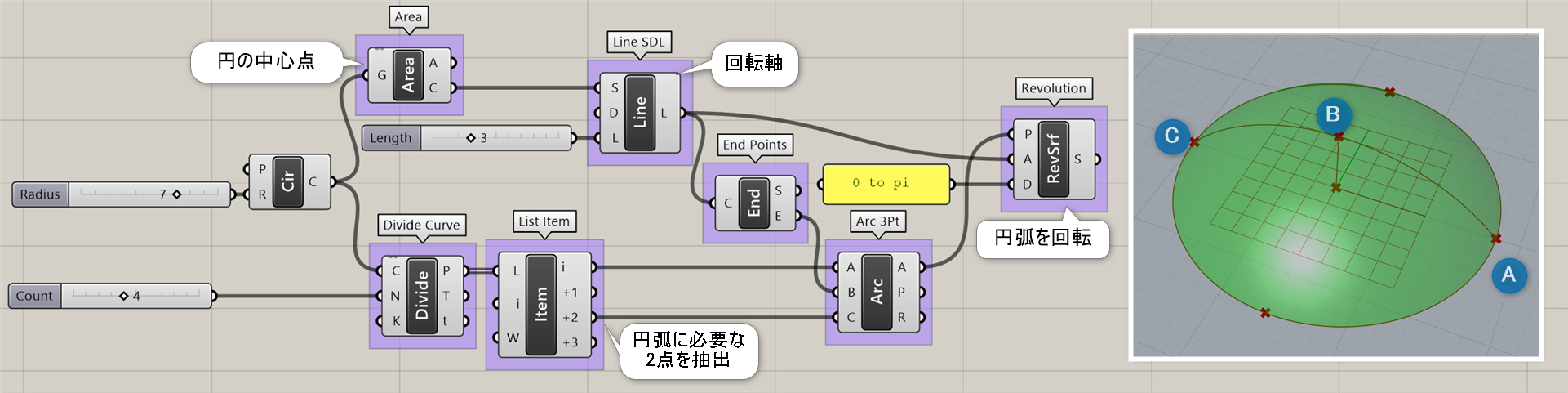
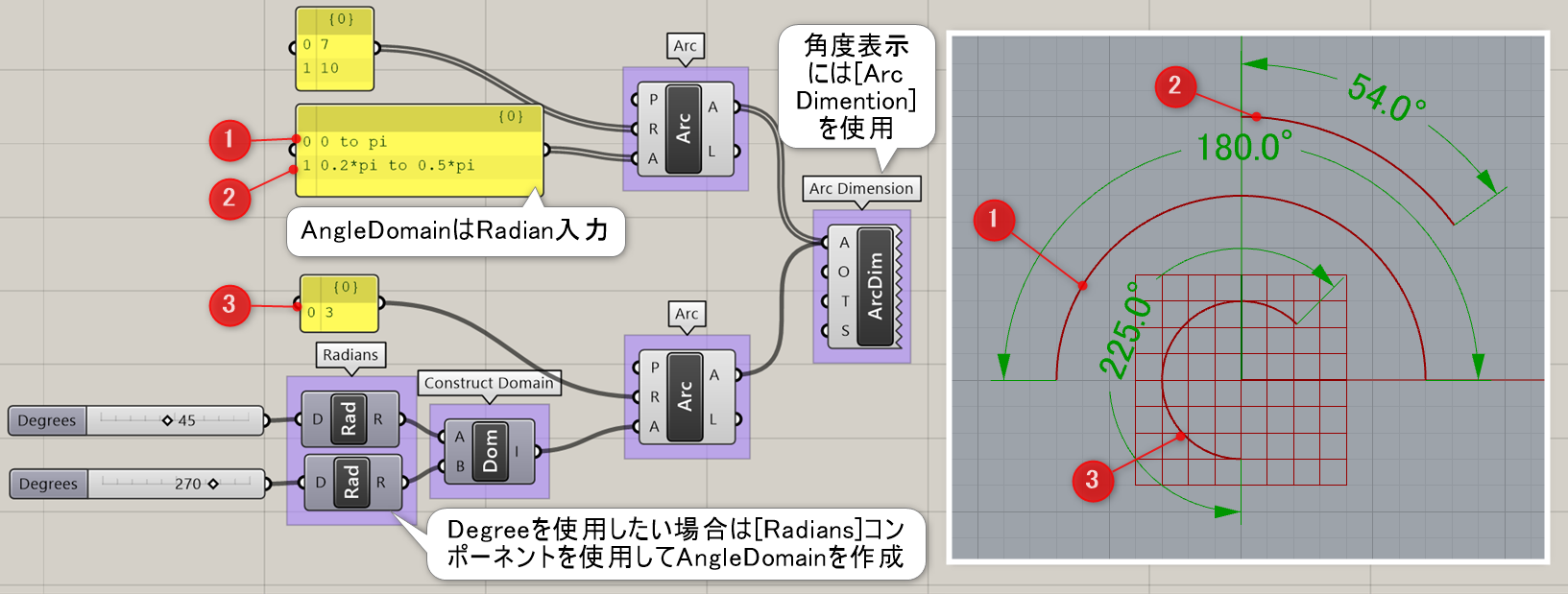
詳細1:基本平面と半径と角度の範囲(ドメイン)により定義された円弧を作成する。半径Rは複数入力可。Aの角度範囲は、ラジアンで入力する。度数で入力したい場合には、事前に[Radians]等で変換しておく。円弧の角度を表示したい場合は、[Arc Dimention]を使用。こちらは度数表記になる。
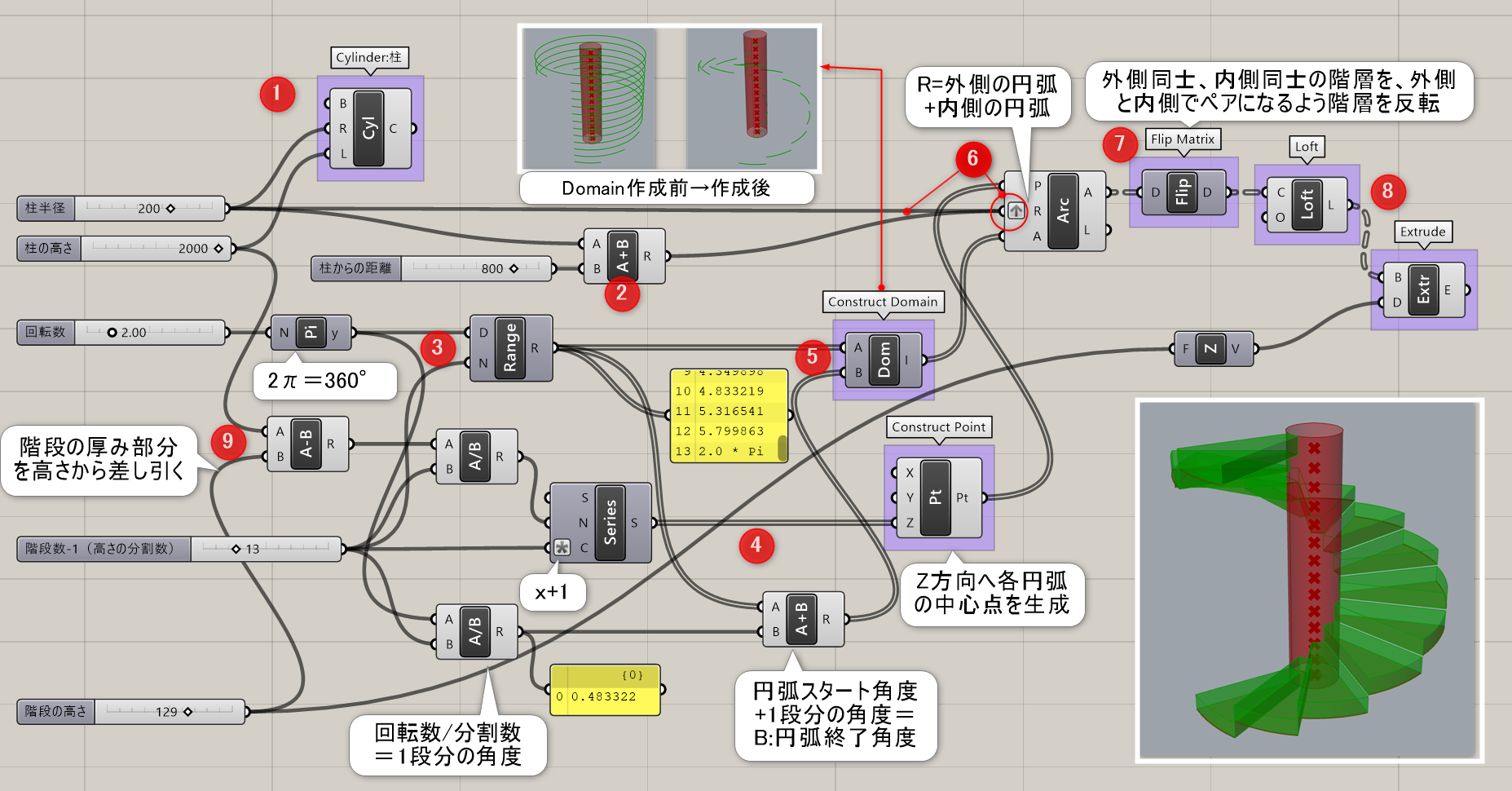
詳細2:[Arc]を利用してらせん階段を作成した例。
①[Cylinder]で柱を作成 ②[Addition]にて、柱の半径からの距離を加えた半径の[Arc]を作成 ③[Range]のドメインに回転数として[Pi]を、ステップ数Nには段数を入力 ④[Series]+[Construct Point]のZ入力で、柱の高さ方向を等分し、Arcの中心点とする ⑤[Construct Domain]で円弧の長さを指定 ⑥[Arc]のR入力に、柱の半径を追加、Graftで階層を分ける ⑦外側の円弧と柱側の円弧をペアにするため[Flip Matrix]で階層を組替え ⑧[Loft]と[Extrude]で面を作成 ⑨柱より段数が高くなるので、柱の高さから階段の厚みを引く。
Arc 3Pt*
B
Curve>Primitive
点(Point)を3つそれぞれ入力し、三点を通る円弧(Arc)、円弧ができる平面(Plane)、円弧の半径(Radius)を出力する。作成される円弧は点Aから始まり点Cで終わる円弧になる。
Arc SED
C

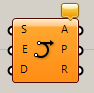
Curve>Primitive
始点(Start)、終点(End)、始点からの接線方向ベクトル(Direction)により定義された円弧(Arc)を作成する。
BiArc
C
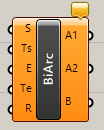
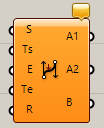
Curve>Primitive
始点(Start)、終点(End)とそれぞれの接線方向ベクトルを入力し、向きを制御した2つの円弧を出力する。1つ目の円弧(A1)、2つ目の円弧(A2)、両方結合した曲線(B)がそれぞれ出力される。
Modified Arc
C
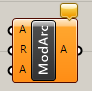

Curve>Primitive
元になる円弧(Arc)と半径(Radius)と範囲(Angle)を指定し、円弧(Arc)を作成する。作成される円弧は、中心点は同じ位置である。
Tangent Arcs
C
Curve>Primitive
円A、B(Circle)と半径(Radius)を入力し、円に接する円弧2つをそれぞれ出力する。
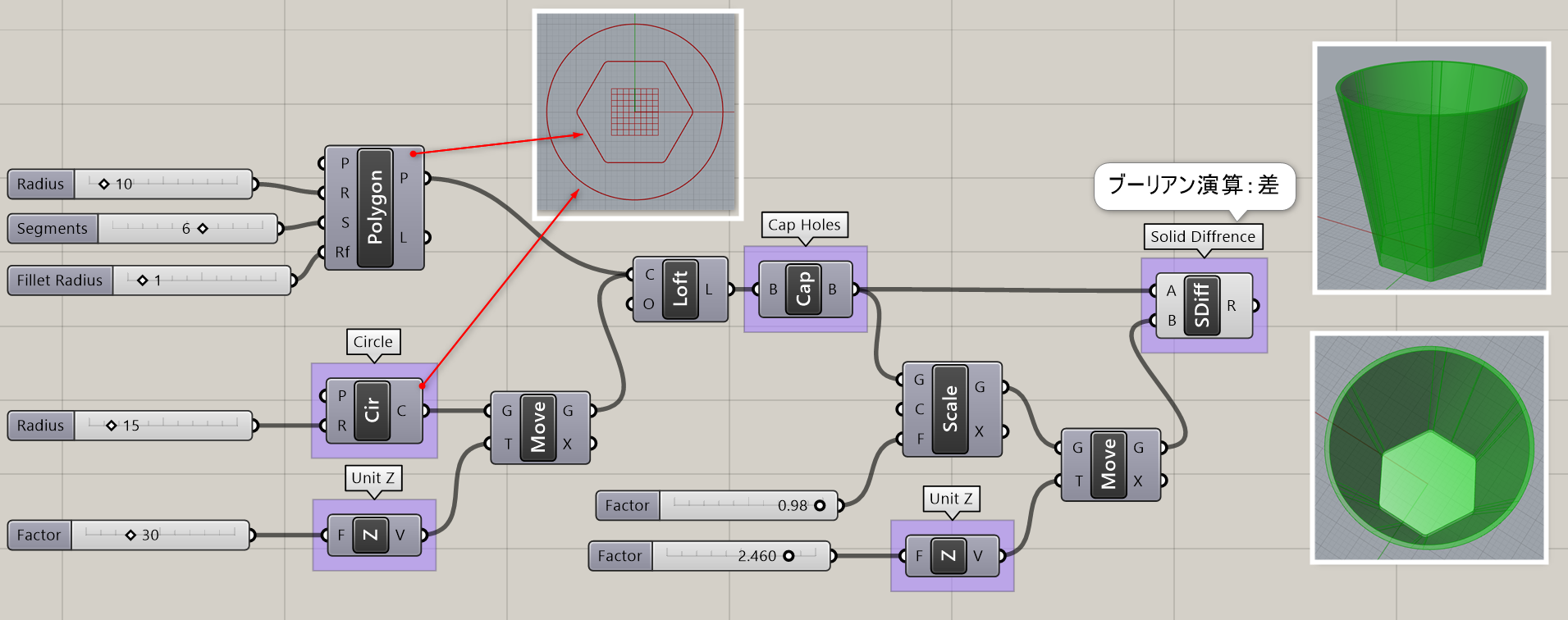
Polygon*
B
Curve>Primitive
平面(Plane)、半径(Radius)、分割数(Segments)などを入力し、円に内接する多角形状の曲線(Polygon)を作成する。オプションで、角部にフィレットを掛ける値も設定できる。
詳細1:基本平面と半径、セグメント(頂点の数)、フィレット半径にて、2次元の多角形を作成する。図は、[Polygon]による六角形と円をロフトでつなぎ、スケールで厚みを付け、[Solid Difference]でブール演算を行った例。
Polygon Edge
C
Curve>Primitive
Rectangle*
B
Curve>Primitive
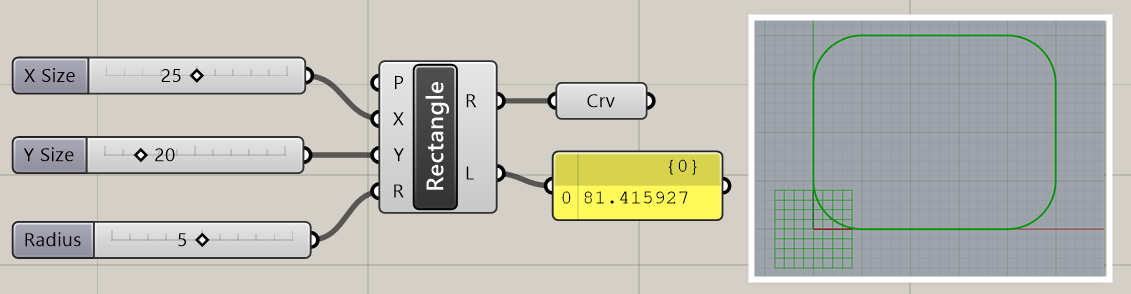
平面(Plane)、X方向Y方向の範囲を入力することで、矩形(Rectangle)とその長さ(Length)を出力する。基本的にはXYは長さではなく、範囲(-10.0 to 25.0)の形で入力する。
詳細1:基本平面Pと、X/Yのサイズで2次元の矩形を作成する。Rで角半径を指定できる。
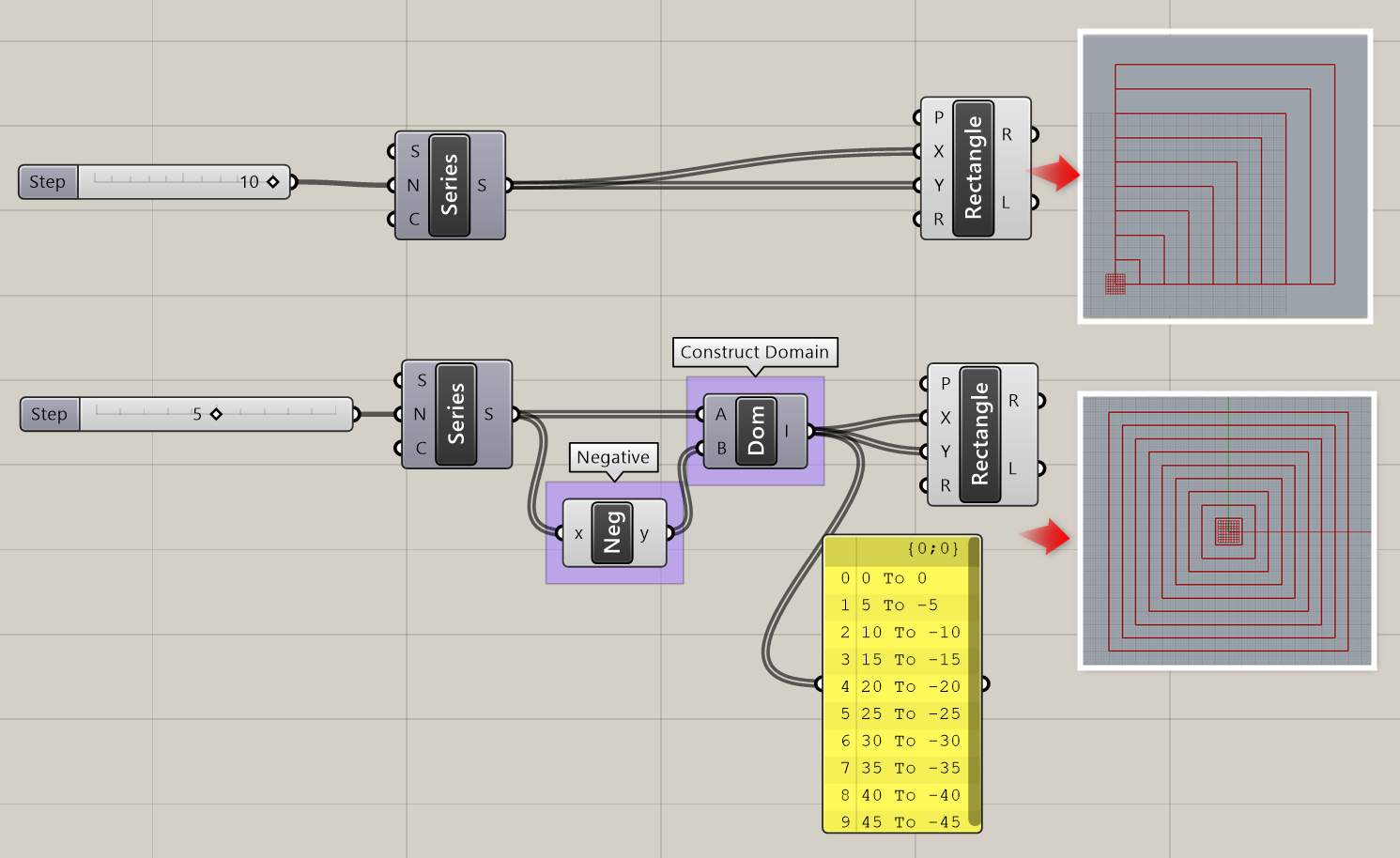
詳細2:サイズの指定は、数値の他ドメインでも指定できる。数値入力の場合は、基本平面の原点が矩形の左角になるが、ドメインを入力すると原点が中心となる。
Rectangle 2Pt
C
Curve>Primitive
平面(Plane)と点(Point)をA,Bに入力することで、2点を通る矩形(Rectangle)とその長さ(Length)を出力する。また矩形は平面上に作成される。
Rectangle 3Pt
C
Curve>Primitive
3点(Point)をそれぞれ入力することで、3点を通る矩形(Rectangle)とその長さ(Length)を出力する。
Spline
Bezier Span*
C
Curve>Spline
点A、B(Point)と各々の接線ベクトルをそれぞれ入力することで、ベジェ曲線(Curve)を作成する。
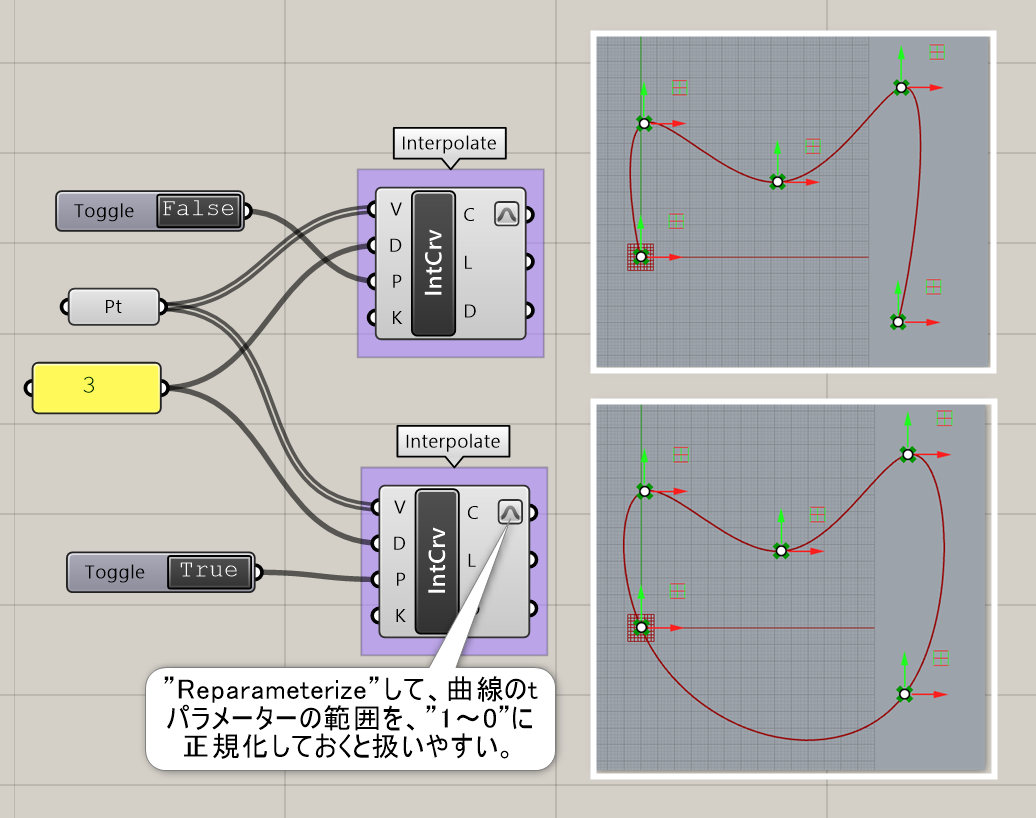
Interpolate*
B
Curve>Spline
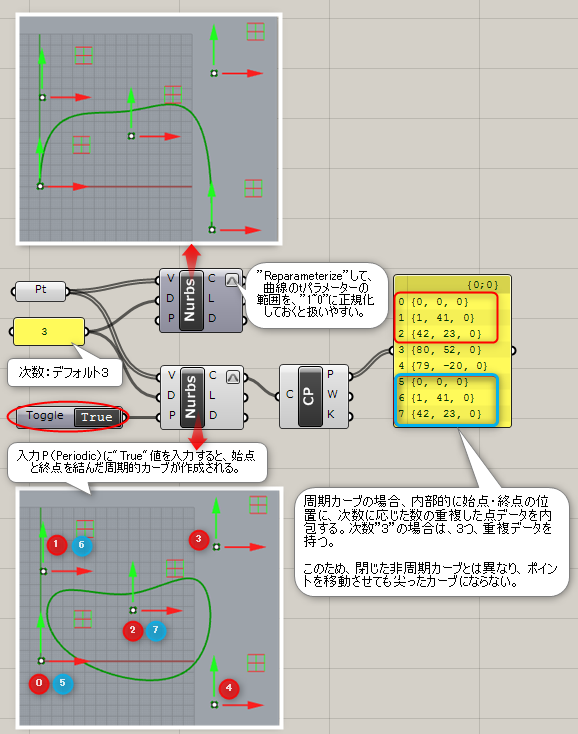
複数の点(Vertices)と次数(Degree)を入力し、点を通過する曲線(Curve)を作成する。オプションで閉じるかどうか(Closed)等も設定できる。Rhinoで言うInterpCrvコマンドと同様の効果。
詳細1:指定した点を通過する曲線を作成する。
点群を入力Vに読み込ませ、入力Dに次数を指定する。(初期値は、”3″)
入力Pに、論理値”True”で点群の始点・終点を結ぶ、周期カーブが生成される。(初期値、”False”)
Interpolate(t)
C
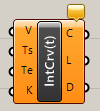
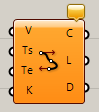
Curve>Spline
複数の点(Vertices)を入力し、点を通過する曲線(Curve)を作成する。オプションで始点の方向ベクトル(Tangent Start)終点の方向ベクトル(Tangent End)なども指定できる。
Kinky Curve
C
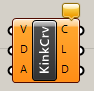
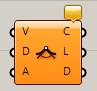
Curve>Spline
複数の点(Verices)、次数(Degree)、しきい値となる角度(Angle)を入力し、しきい値以上の箇所にキンクのある折れた曲線(Curve)を作成する。
Nurbs Curve*
A

Curve>Spline
複数の点(Vertices)と次数(Degree)を入力し、入力点を制御点とする曲線(Curve)を作成する。オプションで閉じるかどうか(Closed)もTrue・Falseで指定できる。Rhinoで言うCurveコマンドと同様の効果。
PolyArc
C
Curve>Spline
複数の点(Vertices)と始点での接線ベクトル(Tangent)を入力し、点を通過し複数の円弧からなる曲線(Curve)を作成する。オプションで閉じる(Closed)かどうかをTrue・Falseで指定できる。
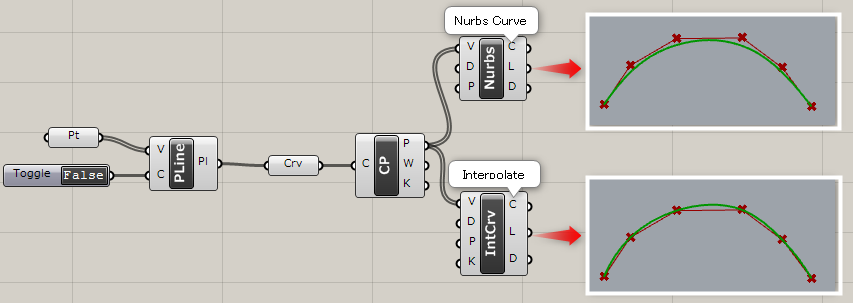
Polyline*
A

Curve>Spline
複数の点(Verticles)を入力し、点を通るポリラインを作成する。オプションでポリラインを閉じるかどうか(Closed)もTrue・Falseで指定できる。
詳細1:入力したポイントからポリラインを作成する。
詳細2:ポリラインを[Control Point]コンポーネントと[NURBS Curve]コンポーネントを使用してカーブに変換した例。[Interpolate]コンポーネントを使用すると、頂点を直接通るカーブになる。
Tangent Curve
C
Curve>Spline
複数の点(Vertices)とそれぞれの点での接線方向(Tangents)を入力し、曲線(Curve)を作成する。ブレンドする強さと次数(Degree)を指定することもできる。
Curve On Surface
C

Curve>Spline
サーフェス(Surface)と複数のUV値を入力し、指定した箇所を通過するサーフェス上の曲線(Curve)を出力する。オプションで、閉じるかどうか(Closed)をTrue・Falseで指定できる。
Geodesic*
B

Curve>Spline
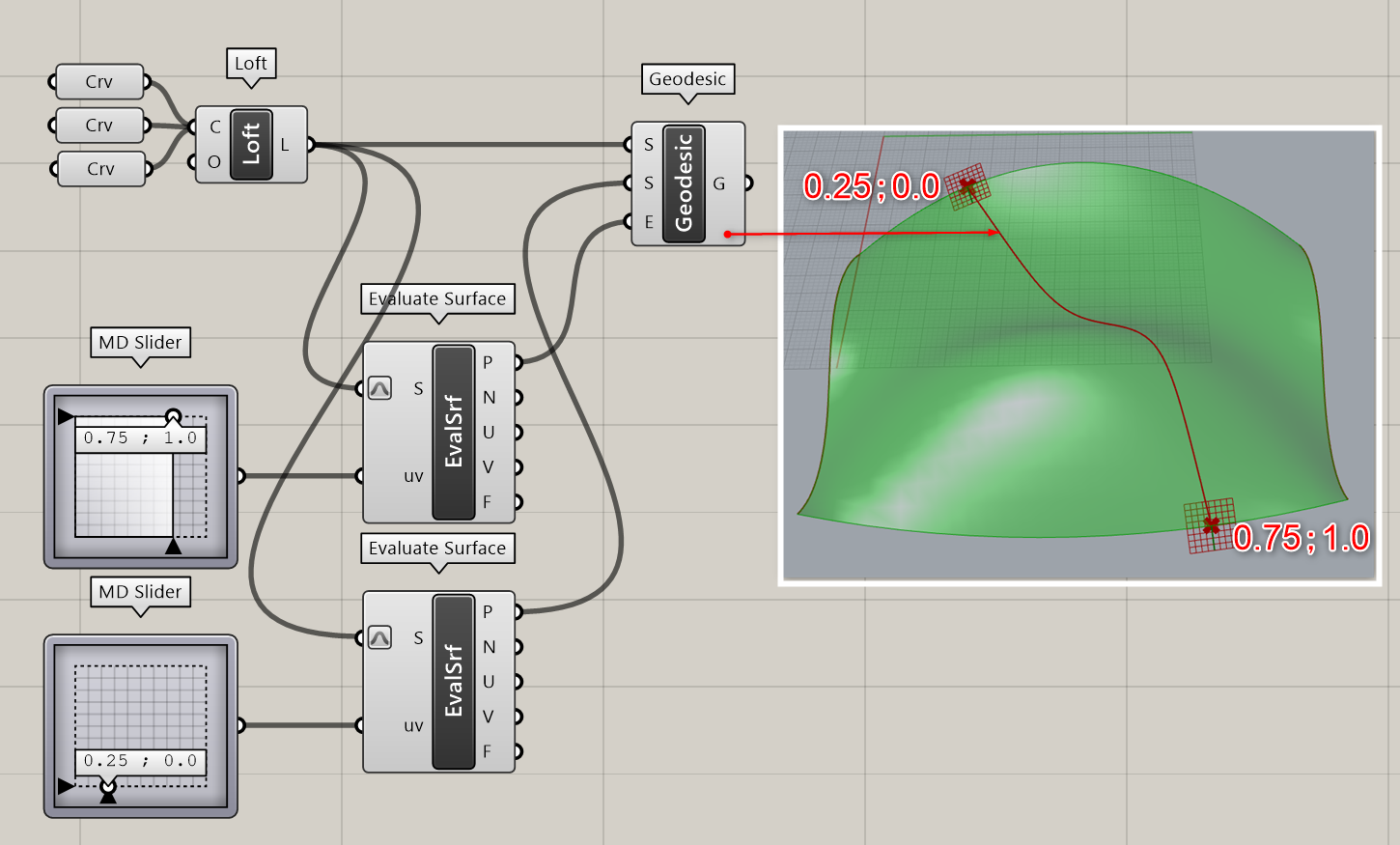
サーフェス(Surface)、始点(Start)、終点(End)を入力し、サーフェス上を最短の距離で結ぶ曲線(Geodesic)を出力する。
詳細1:サーフェス(Surface)、始点(Start)、終点(End)を入力し、サーフェス上を最短の距離で結ぶ曲線(Geodesic/測地線)を出力する。図は、[MD Slider]と[Evaluate Surface]にて指定したポイントを始点/終点に設定し、それを結ぶサーフェス上の曲線を出力した例。
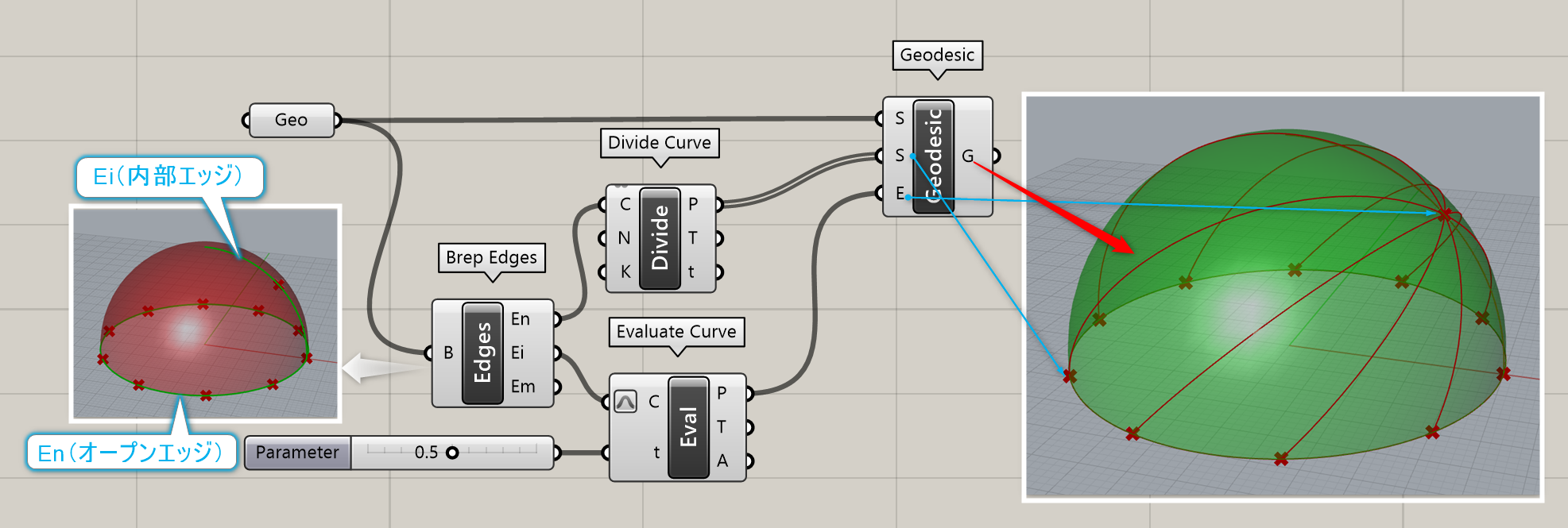
詳細2:ドーム状のオブジェクトのある1点を終点、ドームの底面となる円上の各点を始点として、Geodesic曲線を生成した例。
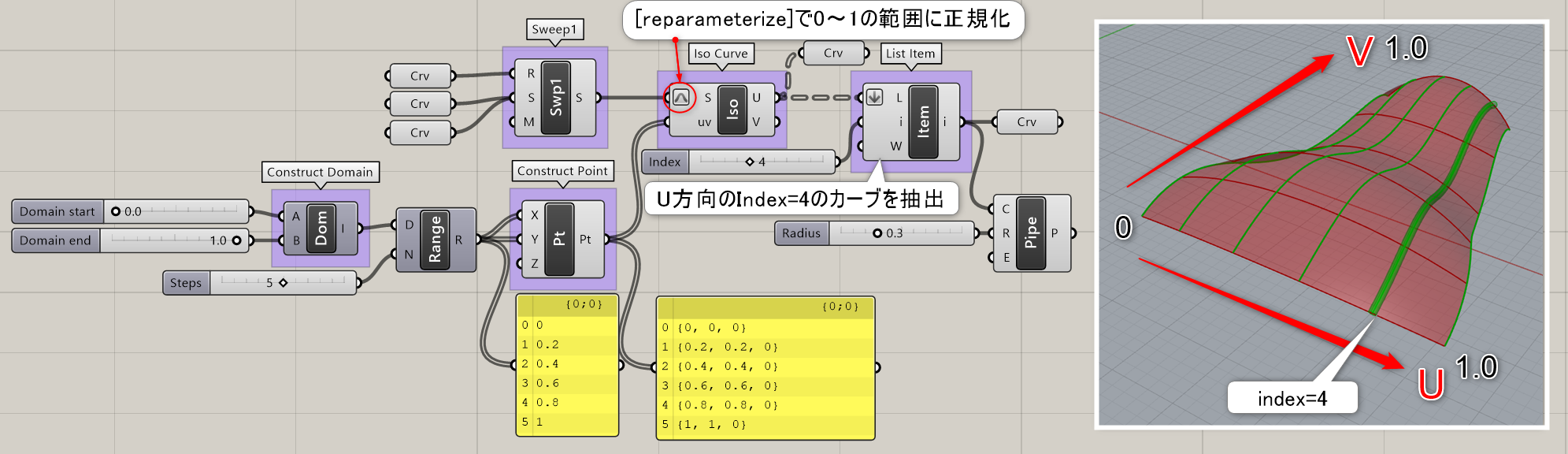
Iso Curve*
B
Curve>Spline
サーフェス(Surface)とUV値を入力することで、指定した位置のU方向、V方向の曲線(Curve)を出力する。
詳細1:サーフェス上のIsoカーブを抽出する。入力したUV座標上のIsoカーブをU/V別に抽出できる。図は、[Construct Domain][Range]と[Construct Point]で作成したUV座標からU方向のIsoカーブを抽出し、[List Item]で更に1本に絞って抽出した例。
Sub Curve
C

Curve>Spline
曲線(Curve)と曲線の取り出したい範囲(Domain)を指定し、短くした曲線を出力する。
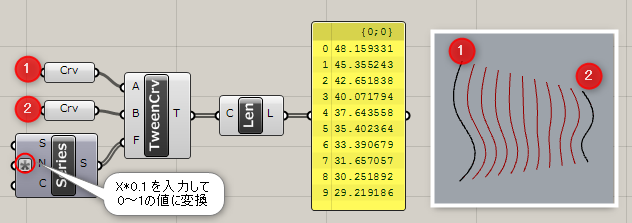
Tween Curve*
A

Curve>Spline
曲線AとB(Curve)、Factorを入力し、AとBをモーフィングするような曲線(Curve)を作成する。Factorが0でAの位置、1だとBの位置に作成される。曲線の向きも重要な為、場合によってはFlipCurveなどで修正すること。
Tips集の詳細ページ
https://www.applicraft.com/tips/rhinoceros/tweencurve/
詳細1:入力した2つの曲線間に、指定した数のTween Curveを作成する。入力FにはカーブAの位置を0、カーブBの位置を1とし、0~1の間で数値を入力すると、その位置にカーブが挿入される。
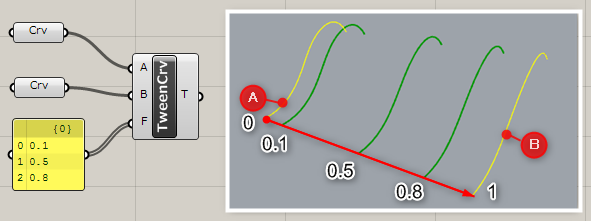
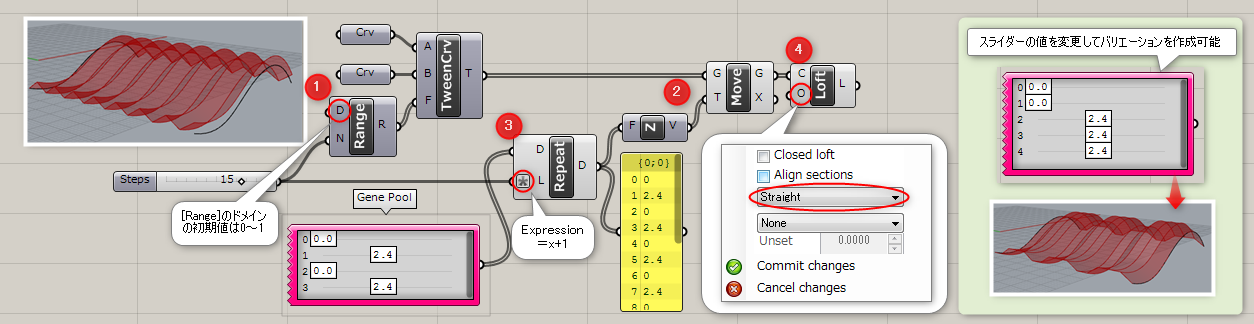
詳細2:Tween Curveを元にLoftでサーフェスを作成した例。
①の入力Fに[Range]コンポーネントで指定した数のカーブを作成
②Z軸方向にカーブを移動
③移動の距離は[Gene Pool]コンポーネントでスライダーにてパターンを作成したものを[Repeat Data]コンポーネントで繰り返す
④[Loft]コンポーネントでオプションを”Straight”にしてサーフェスを作成。
Knot Vector
C
Curve>Spline
制御点(Points)、次数(Degree)、周期(Periodic)を入力し、ノットベクトル(Knots)を作成する。作成されたノットはNurbs Curve PWKなどで使用する。
Nurbs Curve PWK*
B

Curve>Spline
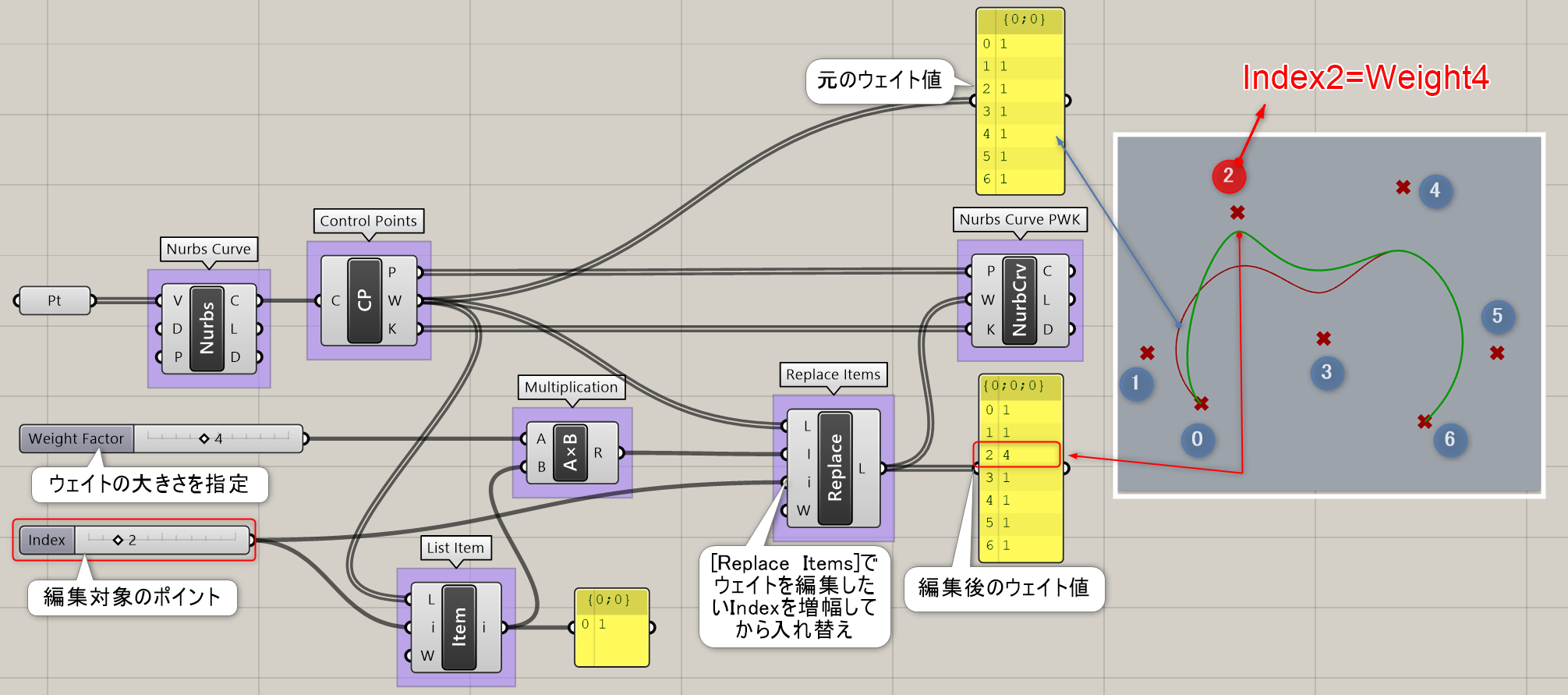
制御点(Points)、ウェイト値(Weights)、ノット(Knots)を入力し、曲線(Curve)を作成する。
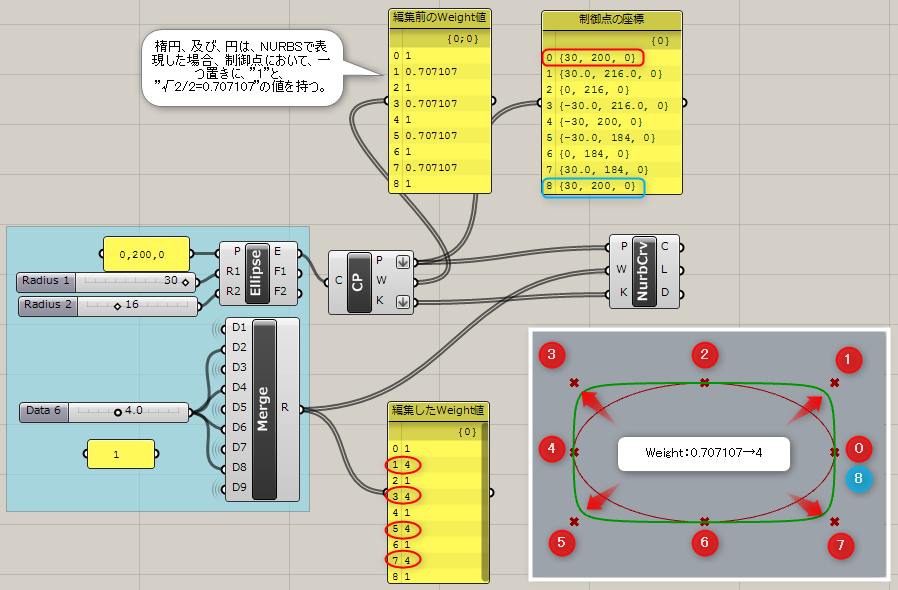
詳細1:制御点(Points)、ウェイト値(Weights)、ノット(Knots)を入力し、曲線(Curve)を作成する。
図は、楕円の要素を抽出後、”Weight”の値を編集して、スーパー楕円を定義した例。
楕円、及び、円は、NURBSで表現した場合、制御点において、一つ置きに、”1”と、”√2/2=0.707107”の値を持つ。
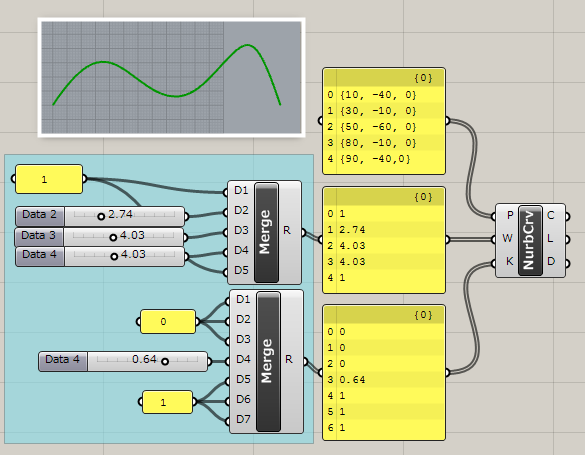
詳細2:”制御点”、”Weight”値、”Knotベクトル”を全て、数値で定義した非周期カーブの例。
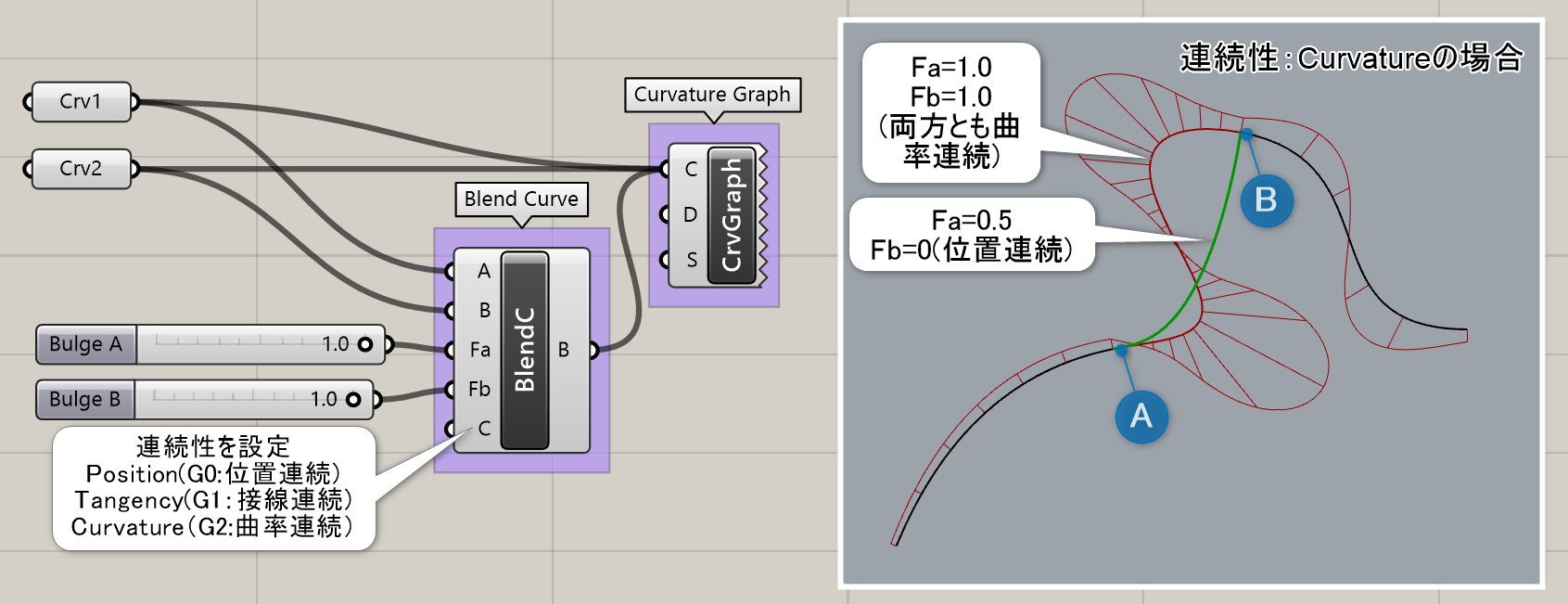
Blend Curve*
B
Curve>Spline
曲線AとB(Curve)を指定し、曲線間を繋ぐブレンド曲線(Curve)を作成する。曲線A,Bの強さ(Buldge)と連続性(Continuity)も指定可能。
詳細1:入力したカーブ間にブレンド曲線を作成する。CrvA側の連続性はFa(BulgeA)で、カーブB側の連続性はFb(BulgeB)で、Cで設定した連続性を1.0として0~1の間で個別に調整できる。
Blend Curve Pt
C
Curve>Spline
曲線AとB(Curve)、通過点(Point)を指定し、曲線間を繋ぐブレンド曲線(Curve)を作成する。連続性(Continuity)も指定可能。
Catenary
C
Curve>Spline
点A、B(Point)、長さ(Length)、重力の方向(Vector)を入力し、カテナリー曲線(Curve)を作成する。曲線の長さをAB間の距離よりも長く設定すること。
Connect Curves*
B
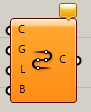
Curve>Spline
複数の曲線(Curves)を入力し、端点同士を結ぶ曲線(Curve)を作成する。オプションで、連続性(Continutitiy)や、閉じるかどうか(Close)、連続性の強さ(Buldge)を指定できる。
詳細1:複数の曲線間を結ぶ曲線を作成する。入力Gでは曲線の連続性を、入力Lではカーブの開閉を指定できる。
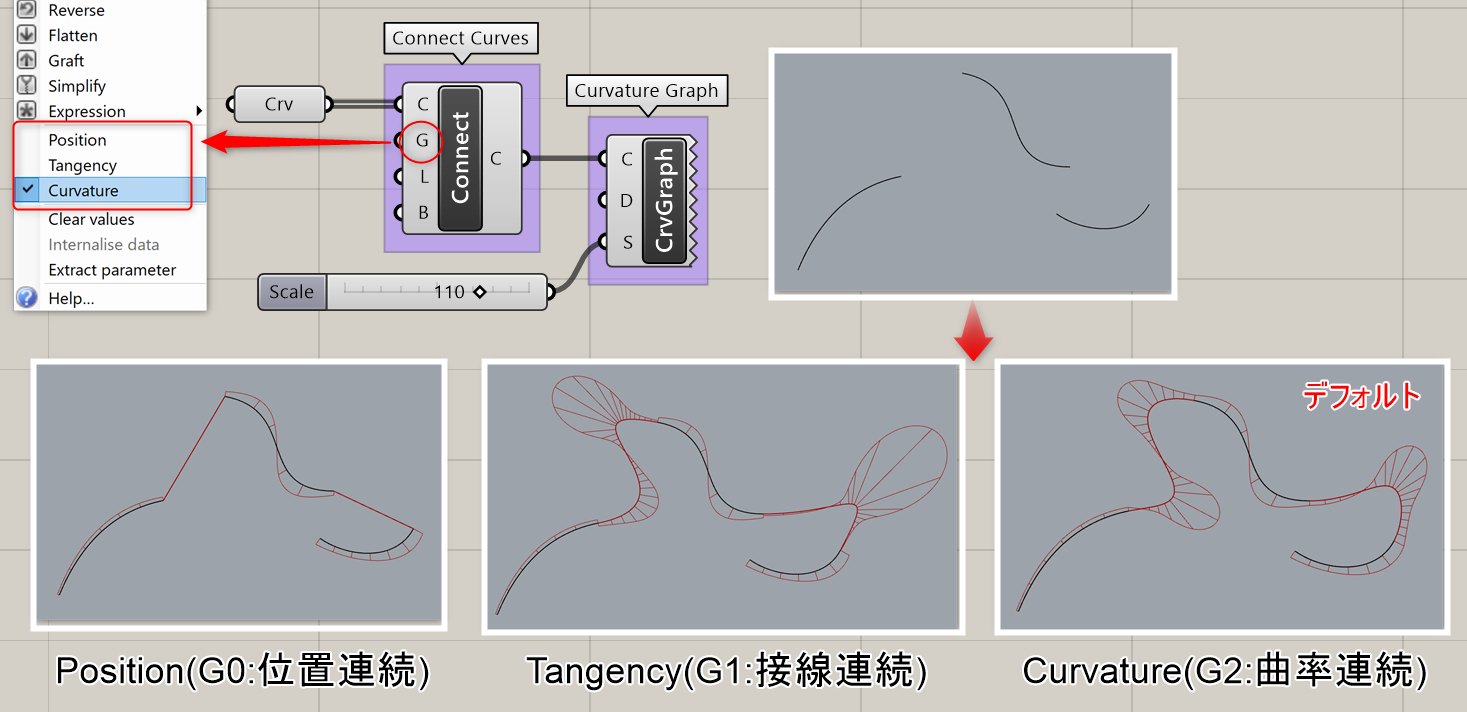
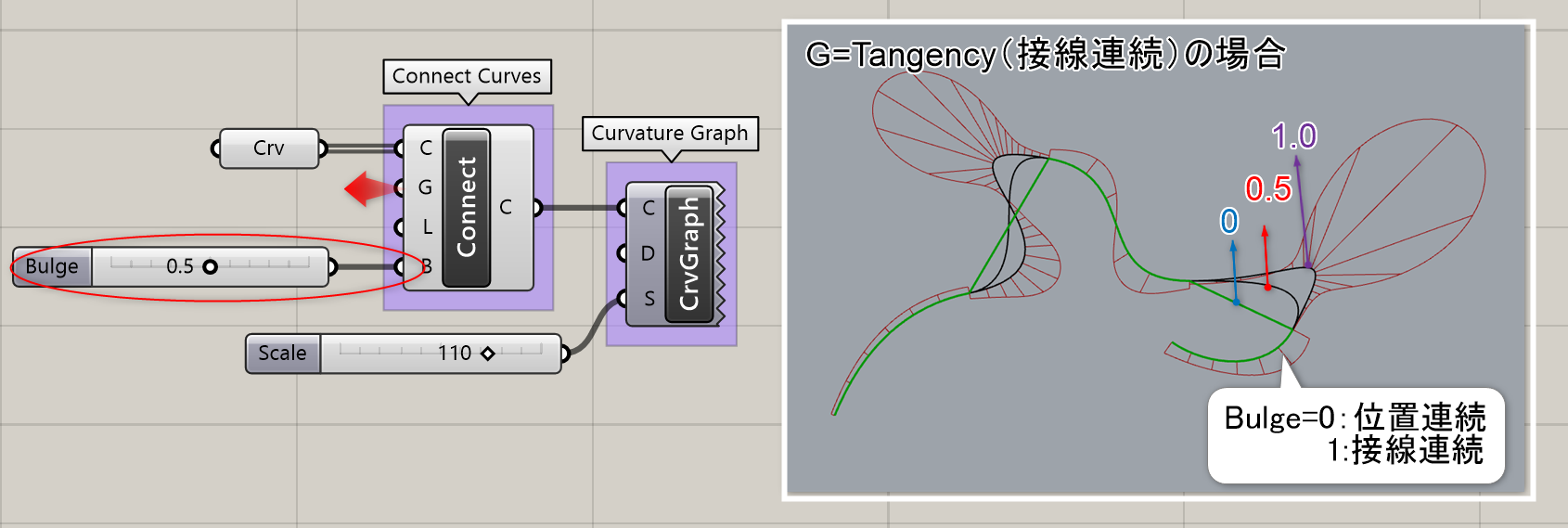
詳細2:入力Bでは指定した連続性を1.0として、0~1の間でバルジ値を調整できる。(例:入力Gの連続性が接線連続の場合は0=位置連続 1=接線連続、連続性が曲率連続の場合は、0=位置連続 1=曲率連続となる)
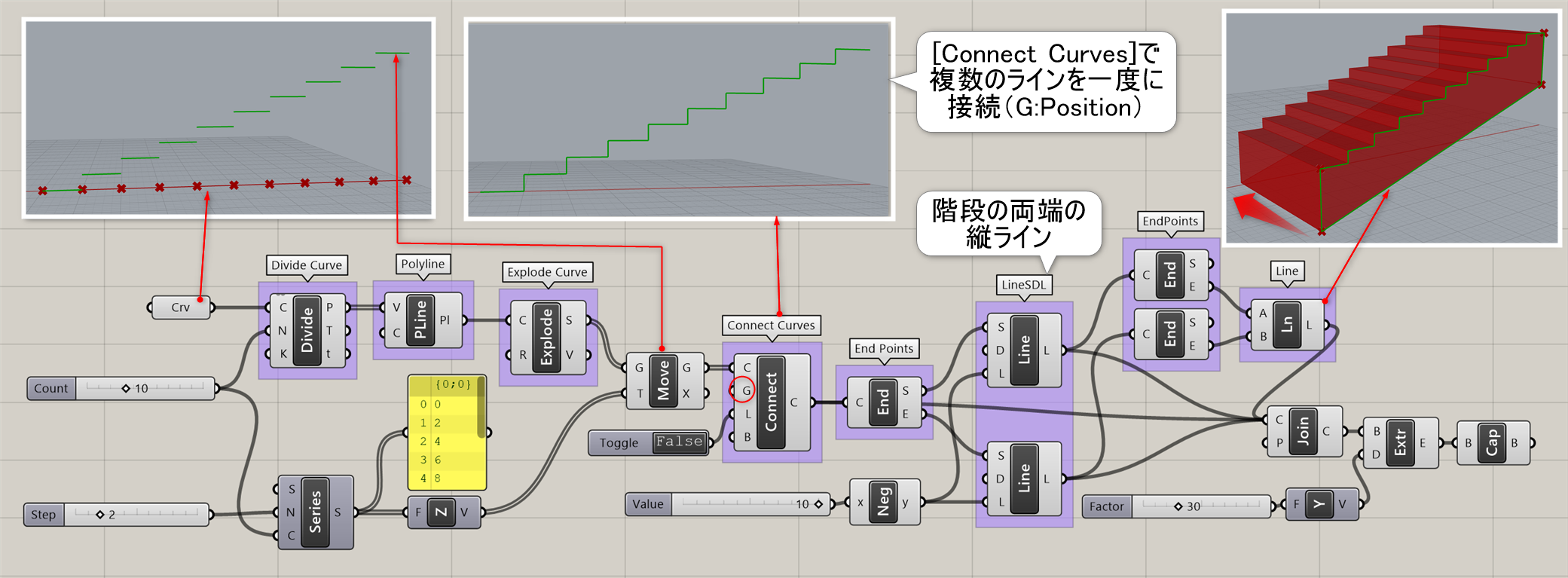
詳細3:[Connect Curves](G=Position、L=False)を使用して、複数の横方向のラインに対して一度に縦のラインを生成し、階段状のラインを作成した例。
Util
Explode*
A


Curve>Util
ポリカーブ状態の曲線(Curve)を入力し、それぞれの曲線(Curve)に分解する。またその分割した点(Verticles)も出力する。ポリサーフェスを分解する場合は、[Deconstruct Brep] などを使うこと。
詳細1:入力カーブを、元の要素(ポリカーブ、ポリライン等)またはセグメントに分解する。
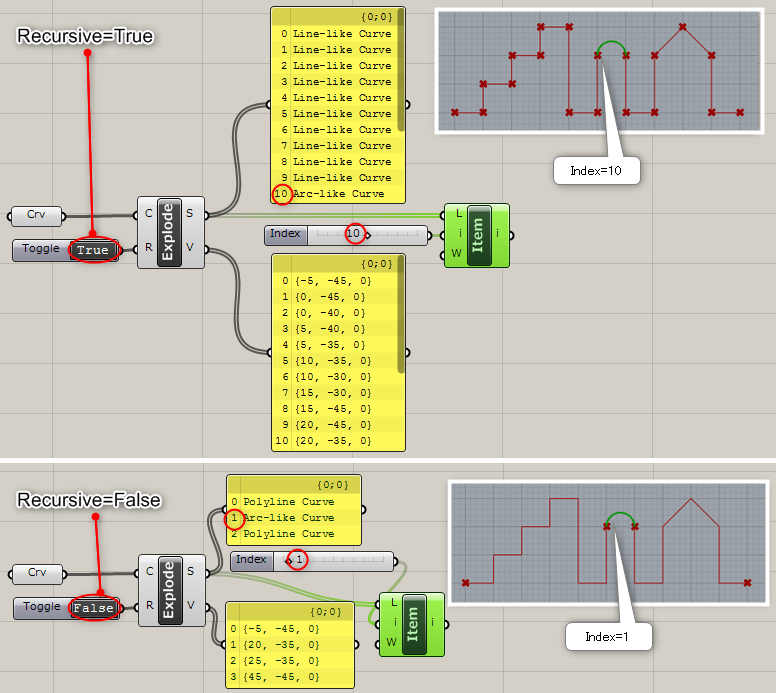
入力Rが”True(初期値)”の場合は、最小セグメントまで分解する。”False”の場合、元のポリライン/ポリカーブの単位で分解する。出力Sはセグメント、出力Vは頂点の座標を出力する。図は、[List Item]コンポーネントで円孤のカーブ部分を抽出した例。
Extend Curve*
B

Curve>Util
曲線(Curve)、延長方法(Type)、始点(L0)と終点(L1)の延長値をそれぞれ入力することで、曲線を延長する。L0とL1の両方に値が入っていないと、コンポーネントが働かない為、注意が必要。
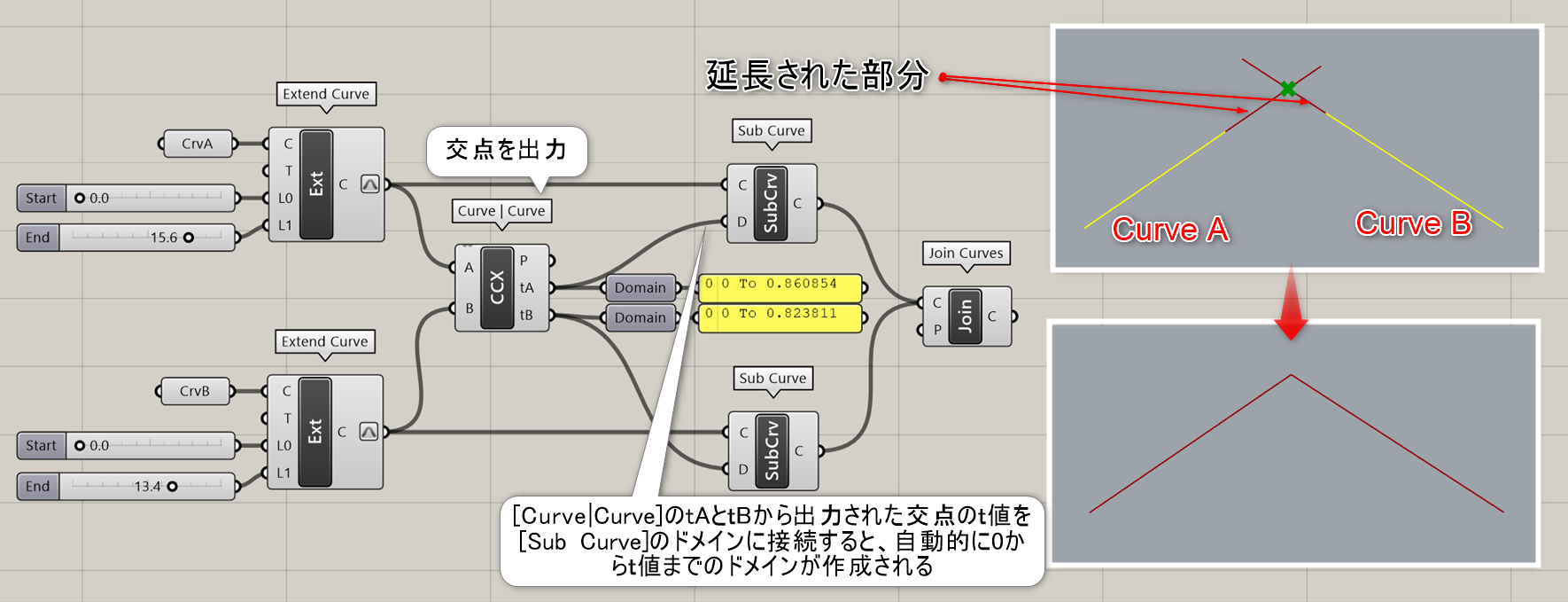
詳細1:曲線(Curve)、延長方法(Type)、始点(L0)と終点(L1)の延長値をそれぞれ入力することで、曲線を延長する。図は、2本のラインを[Extend Curve]で延長し、[Curve | Curve]で取得した交点のt値を利用して[Sub Curve]で交点までの長さにラインを整えた例。
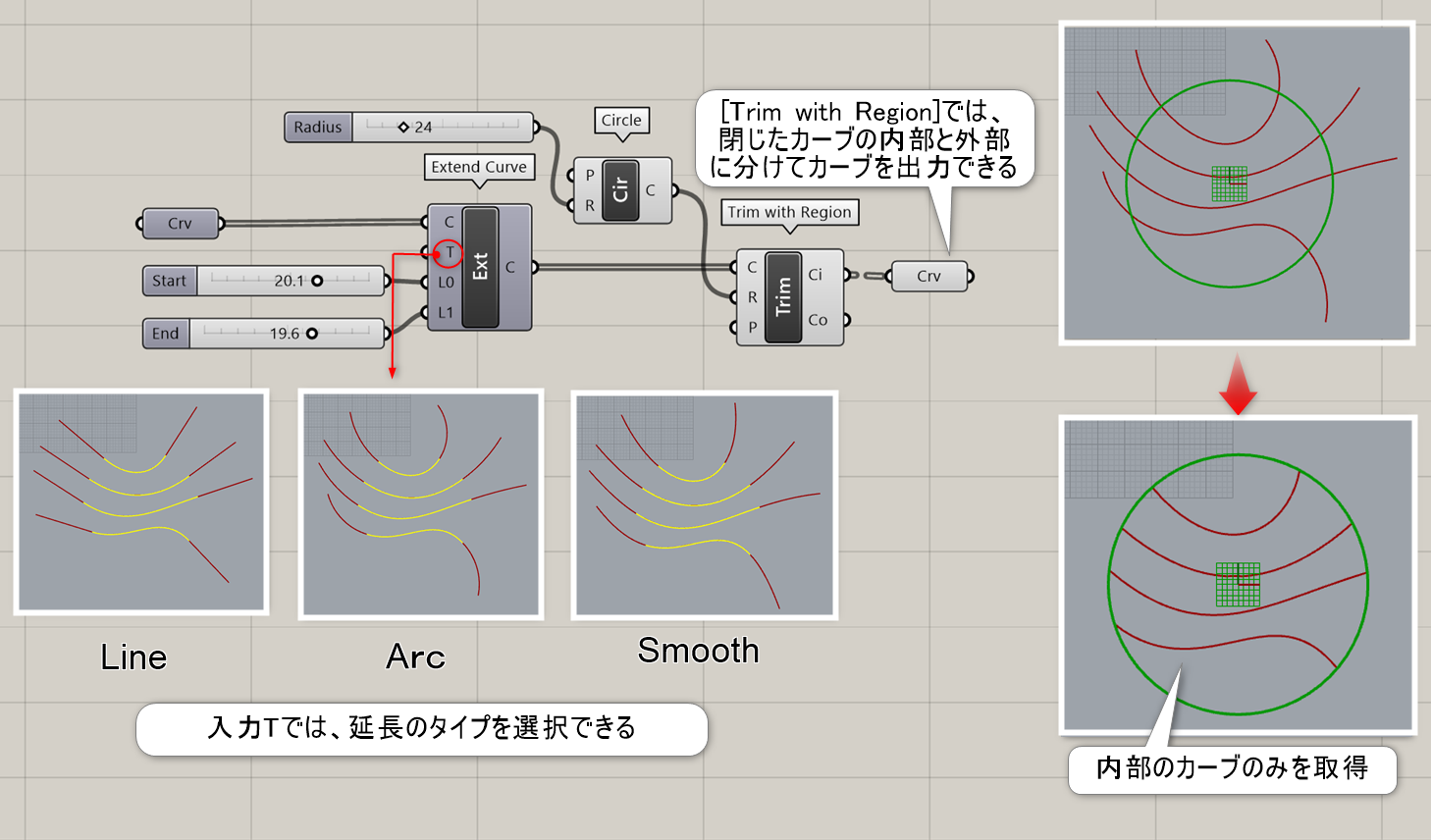
詳細2:曲線の延長タイプを変更し(ここではArc)、[Trim with Region]を使用して境界(ここでは円)まで延長させた例。
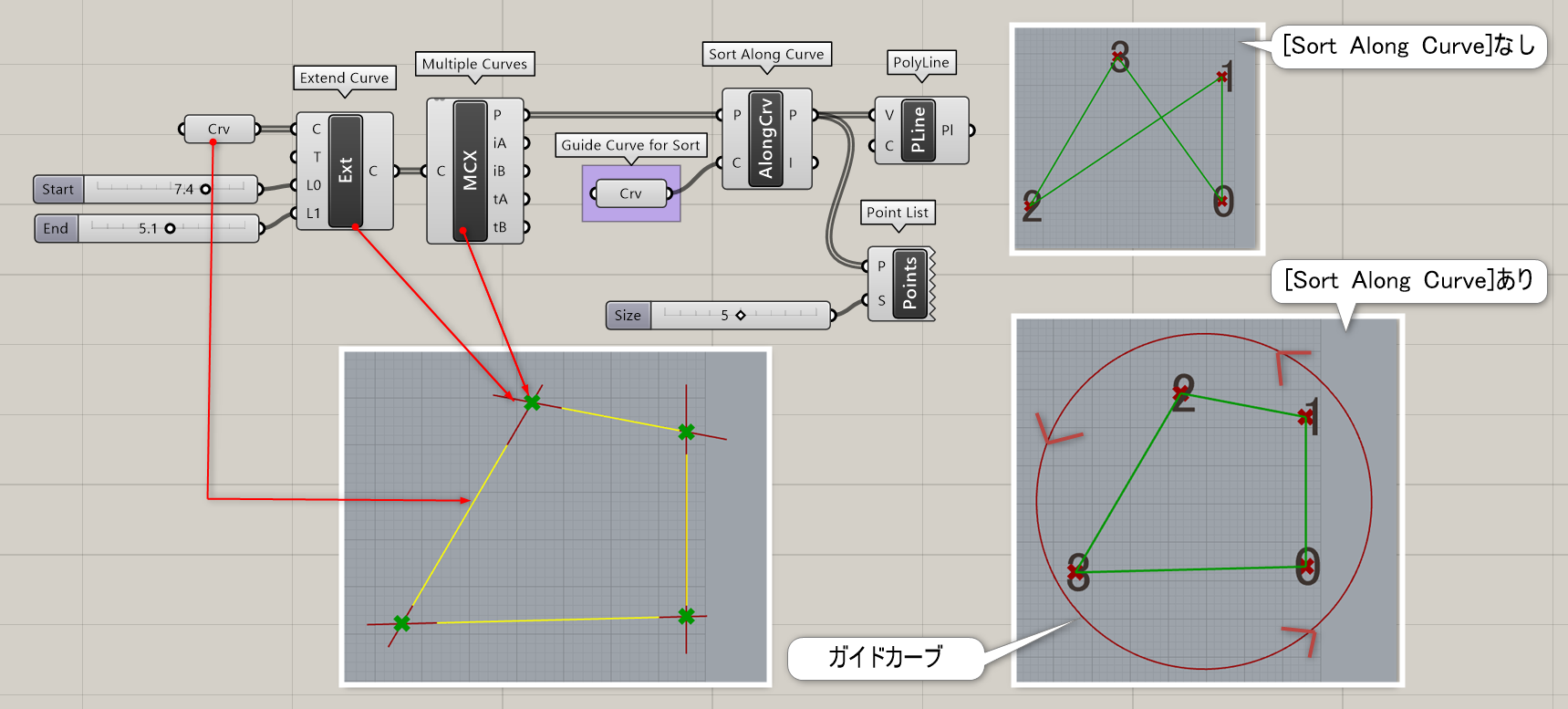
詳細3:複数曲線を延長してできた交点を元に、新たにポリラインを作成する事で延長部分を削除した例。[Sort Along Curve]を使用して、一方向に向きの揃ったカーブ(ここでは円)をガイドとしてポイントの接続順を修正している。
Flip Curve*
A


Curve>Util
入力した曲線(Curve)の向きを反転する。オプションでガイドとなる曲線(Guide)を入力し、ガイド曲線と向きを揃えることもできる。
詳細1:カーブの始点と終点を反転する。
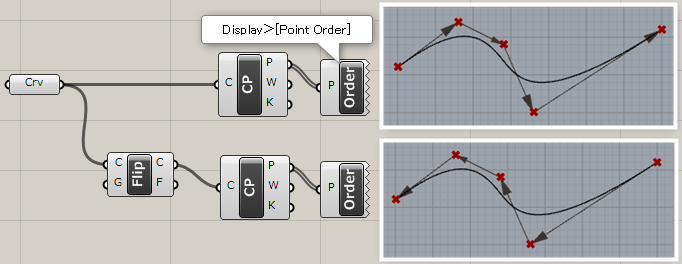
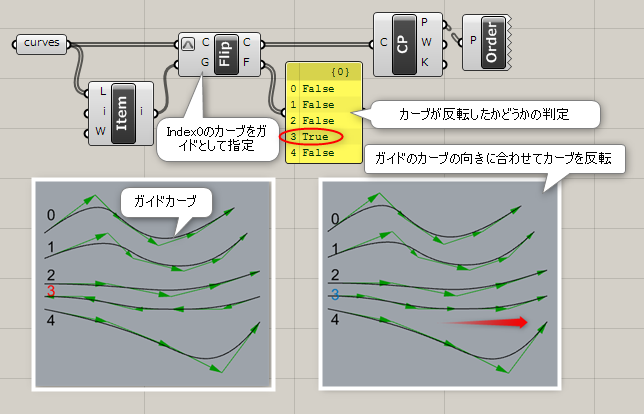
詳細2:入力Gにガイドカーブを指定すると、そのカーブの向きに合わせて入力カーブを反転させる。出力Fからはカーブを反転させたかどうかをTrue/Falseで判定する。
Join Curves*
A


Curve>Util
端点が許容差以内の複数の曲線(Curves)を一つの曲線に結合する。サーフェスなどを結合する時は、[Brep Join]を使用すること。
詳細1:端点の一致した複数のカーブを結合して、ポリカーブとして出力する。図は複数カーブを結合し、[Move]コマンドでY方向に移動した例。
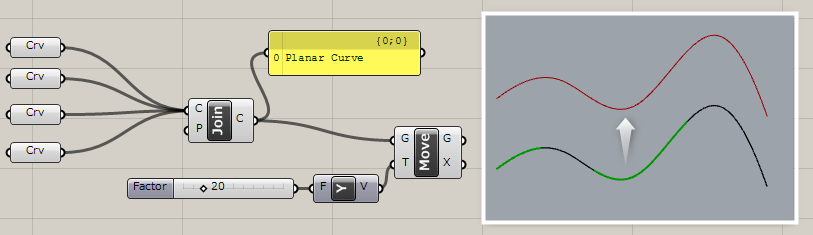
詳細2:入力PのPreserveに”True”値を入力すると、カーブの向きを保存する事ができる。これにより、grasshopperが判定した同じカーブの向きのカーブ同士が結合される。
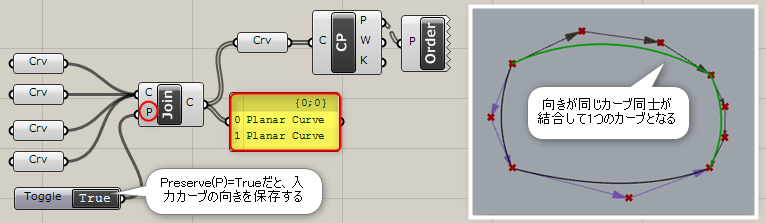
Fillet*
B


Curve>Util
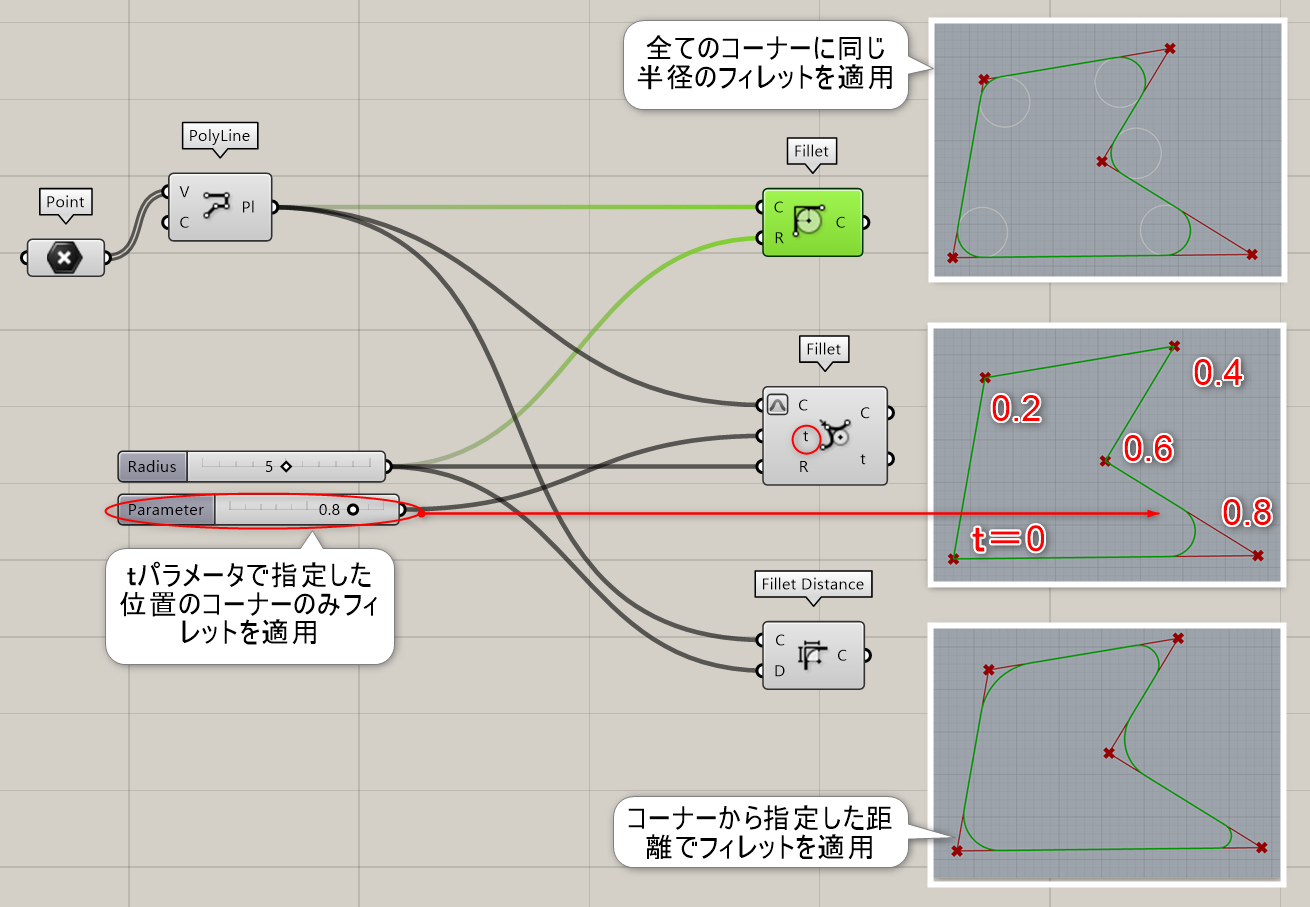
曲線(Curve)と半径(Radius)を入力し、角部にフィレットを付けた曲線(Curve)を作成する。
詳細1:曲線(Curve)と半径(Radius)を入力し、角部にフィレットを付けた曲線(Curve)を作成する。同名のコンポーネント(図中央)があるが、そちらはtパラメータを指定して、フィレットを適用するコーナーを指定できる。また、類似したコンポーネントに[Fillet Distance](図下)があり、コーナーからの距離を指定してフィレットを適用する。
Fillet
C
Curve>Util
曲線(Curve)とtパラメータ値を入力し、指定箇所に半径(Radius)フィレットを作成する(1つ上のFilletの詳細に使用方法記載あり)。
Fillet Distance
C


Curve>Util
曲線(Curve)を入力し、すべての角部に距離(Distance)が一定となるフィレットを作成する。角の頂点からフィレットが始まる点までの長さが一定になる(22つ上のFilletの詳細に使用方法記載あり)。
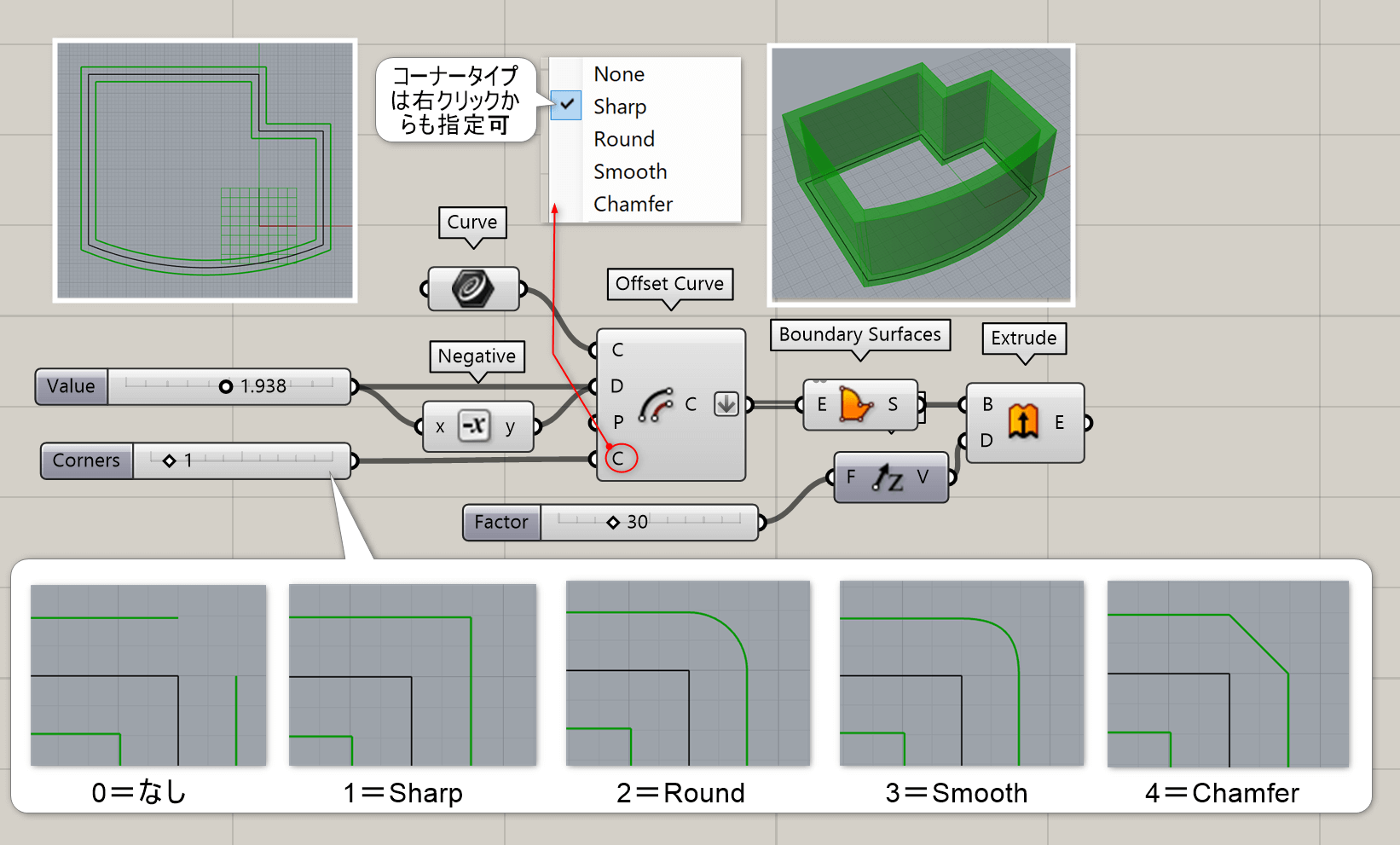
Offset Curve*
A
Curve>Util
曲線(Curve)と距離(Distance)を入力し、指定距離オフセットした曲線(Curve)を作成する。オプションとして計算基準となる平面(Plane)や、角部の処理もCornersから指定できる。
詳細1:曲線(Curve)と距離(Distance)を入力し、指定距離オフセットした曲線(Curve)を作成する。オプションとして計算基準となる平面(Plane)や、角部の処理もCorners(右クリックまたは0~4の数値入力)から指定できる。図は、カーブの入力に[Negative]を追加し、元の曲線を中心として厚みをつけるようにオフセットした例。
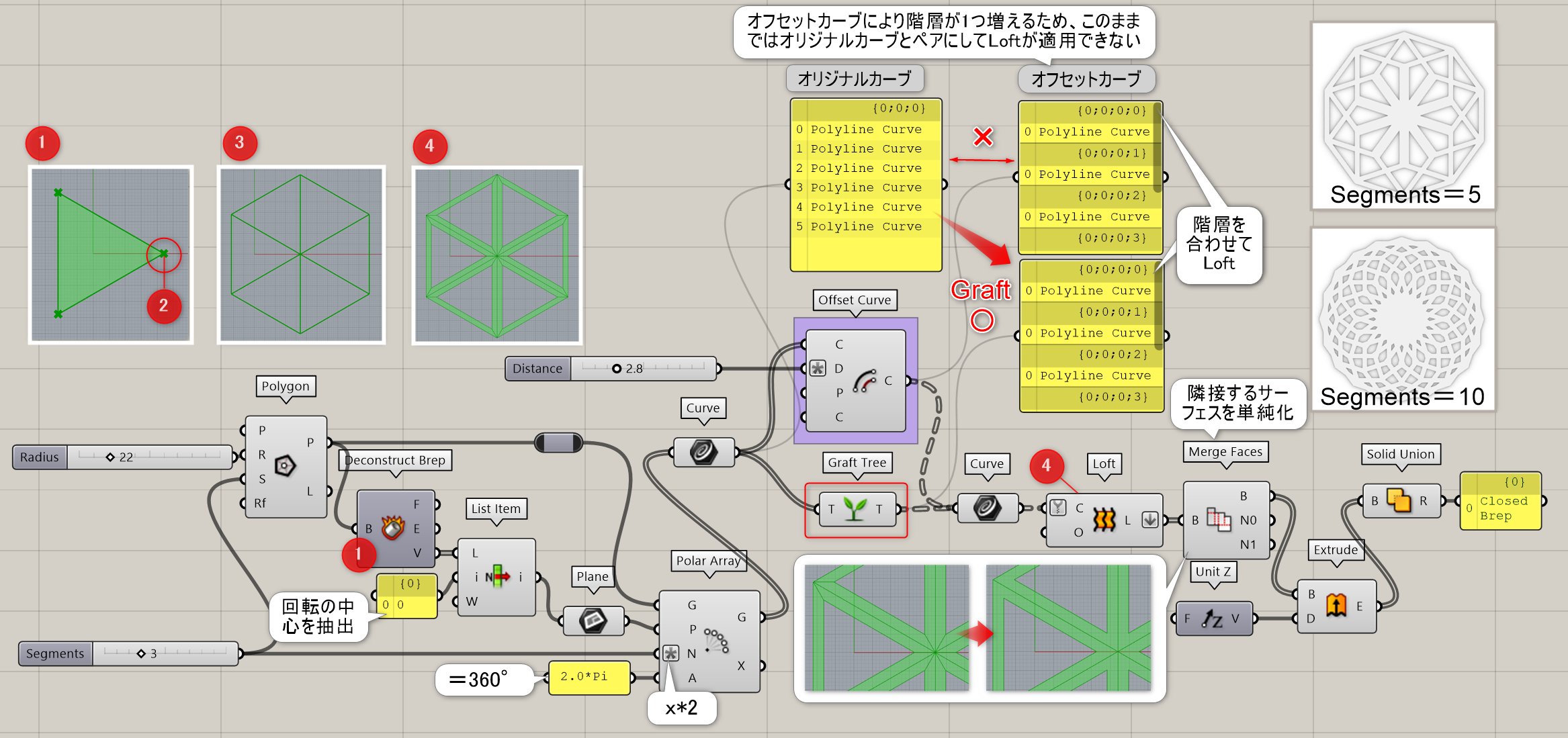
詳細2:多角形を回転させて作成したカーブに[Offset Curve]を適用し、元のカーブとオフセットカーブの間に[Loft]でサーフェスを作成した例。[Offset Curve]を適用すると階層が1つ増えるため、元のカーブに[Graft Tree]を適用して階層を揃えている。
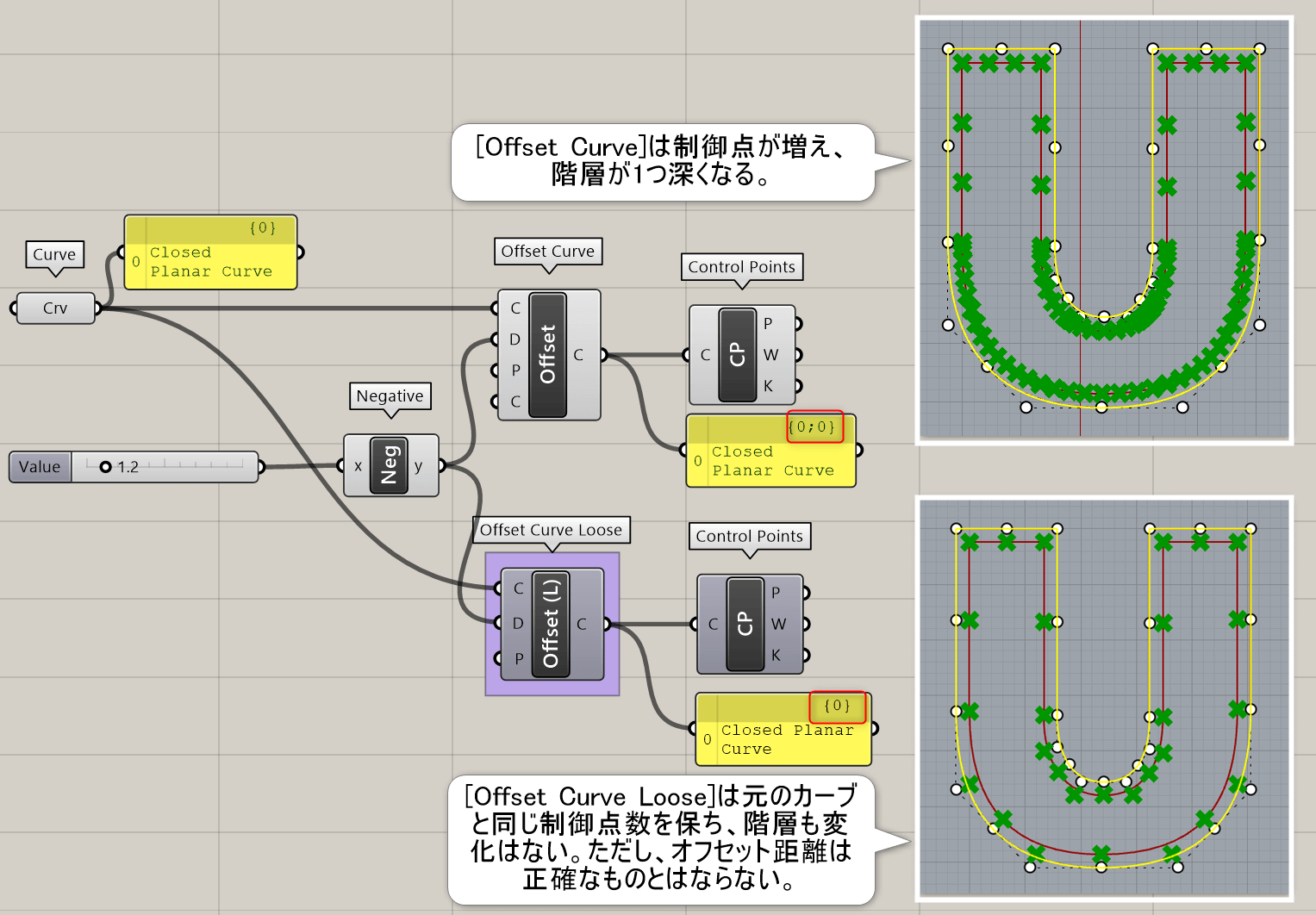
Offset Curve Loose*
A
Curve>Util
曲線(Curve)と距離(Distance)を入力し、制御点を増やさない様にオフセットした曲線(Curve)を作成する。制御点を増やさない為、オフセット距離は完全に指定した値ではないことに注意。
詳細1:曲線(Curve)と距離(Distance)を入力し、制御点を増やさない様にオフセットした曲線(Curve)を作成する。制御点を増やさない為、オフセット距離は完全に指定した値ではないことに注意。また、[Offset Curve]を適用すると階層が1つ深くなるが[Offset Curve Loose]では階層に変化はない。
詳細2:サーフェスのエッジを抽出し、[Offset Curve]ではうまくオフセットできなかった場合に[Offset Curve Loose]で形状を保つ事ができる場合がある。それでも、形状やオフセット値によっては自己交差が起こってしまった場合に、[Python Script]にて修正した例。
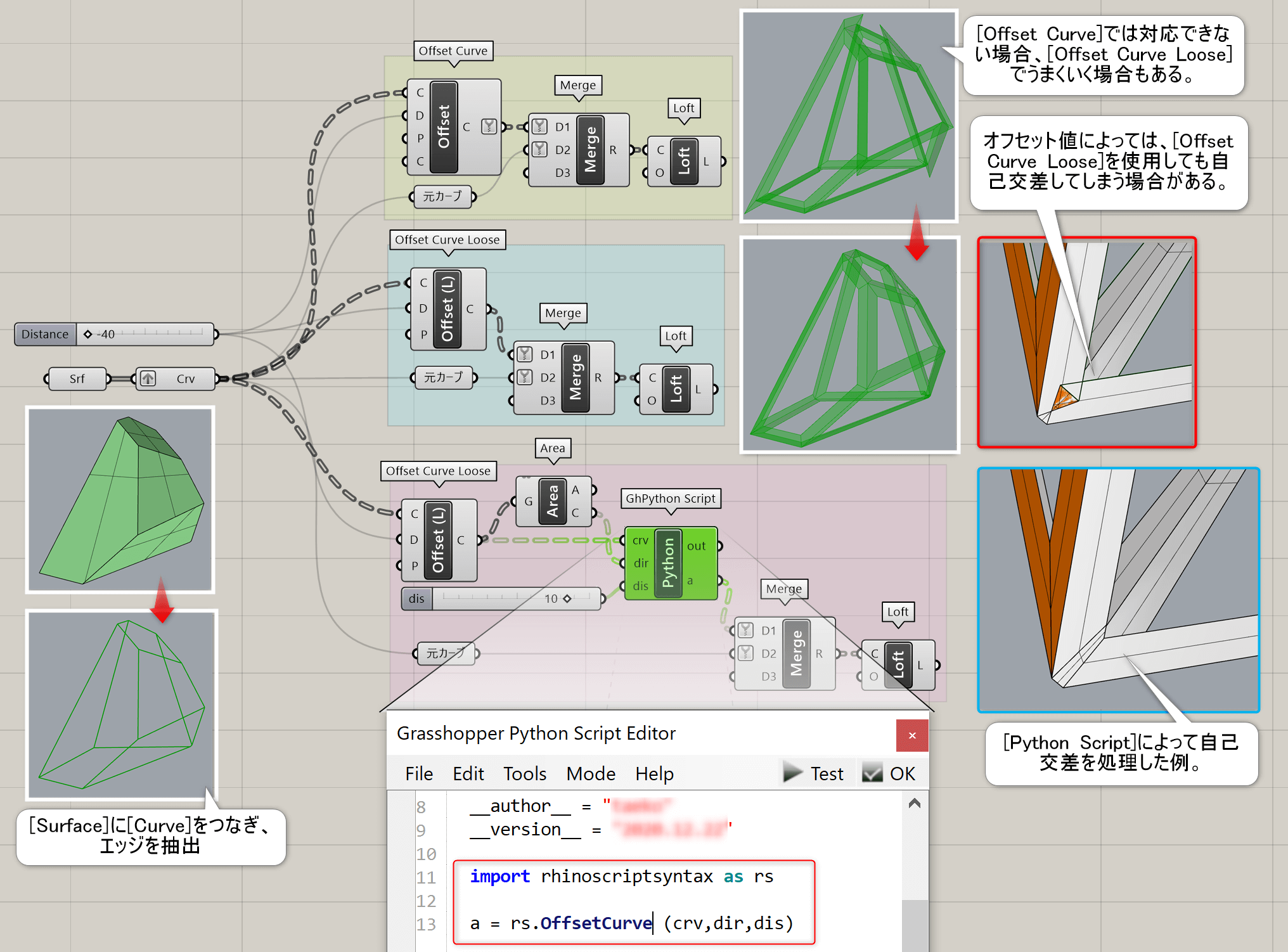
Offset on Srf*
A


Curve>Util
曲線(Curve)を、サーフェス(Surface)上で指定した距離(Distance)オフセットする。
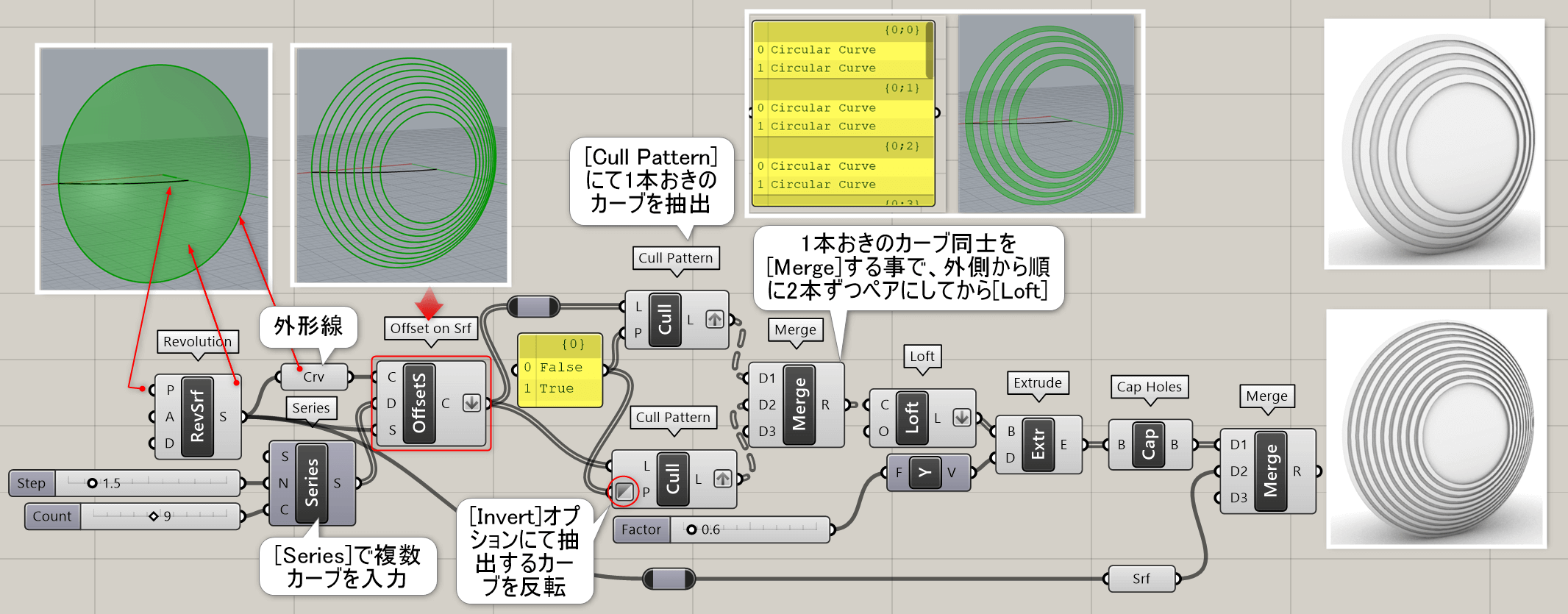
詳細1:曲線(Curve)を、サーフェス(Surface)上で指定した距離(Distance)オフセットする。図は、[Revolution]で作成したサーフェスの外形線を[OffsetOnSrf]で内側に複数オフセットして作成したカーブを、[Cull Pattern]を使用して2本ずつペアにして[Loft]でサーフェスを張り、[Extrude]で押し出した例。
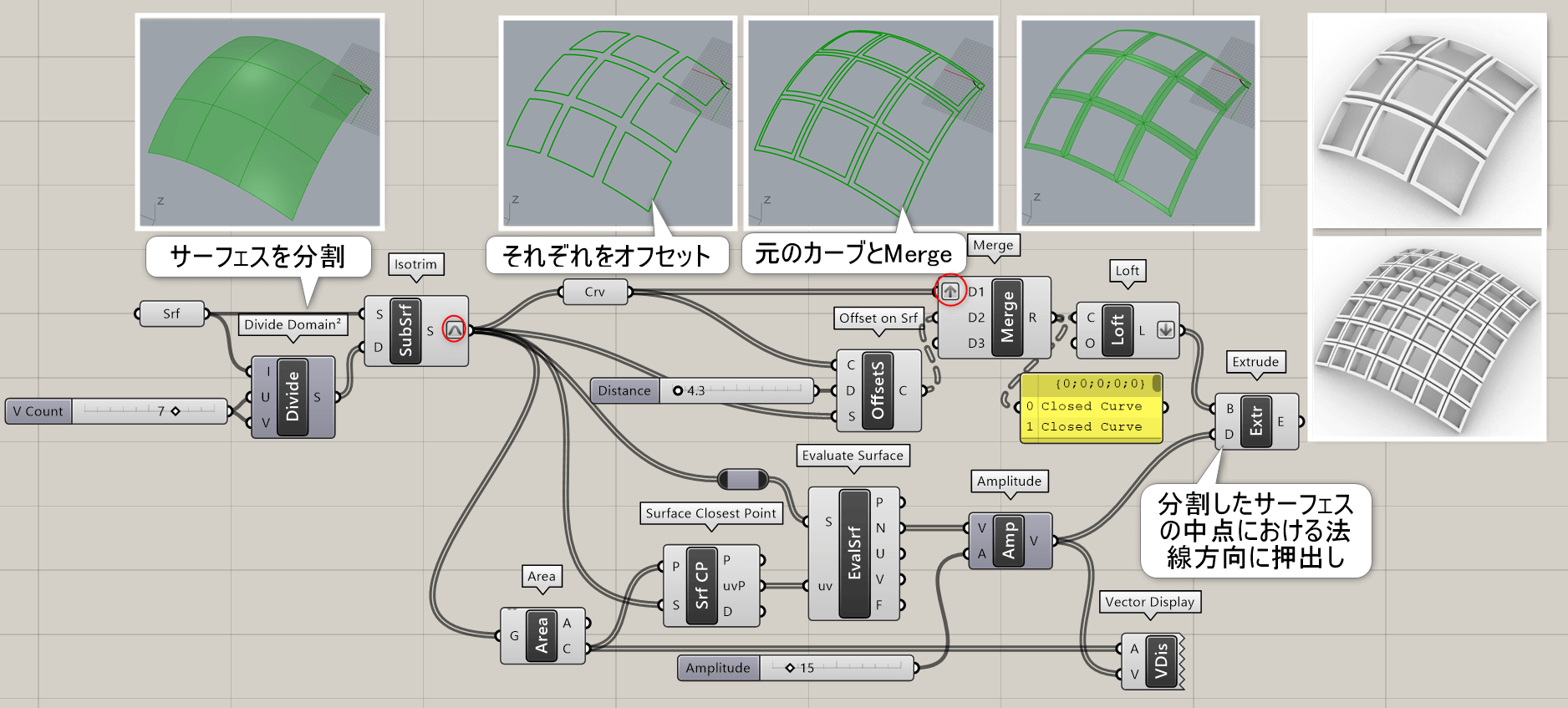
詳細2:サーフェスを[Divide Domain²]で分割し、それぞれのサーフェスを[Offset On Srf]でオフセットしたカーブと元のカーブ間に[Loft]でサーフェスを張って押し出した例。押出す方向は[Surface Closest Point]と[EvaluateSrf]で法線方向を取得している。
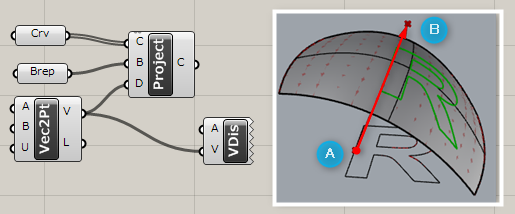
Project*
A
Curve>Util
曲線(Curve)とBrep、方向ベクトル(Direction)を指定し、Brep上に投影した曲線(Curve)を作成する。
詳細1:入力Bで指定したBrepオブジェクトに、入力Cで指定したカーブを投影し、出力Cからそのカーブを出力する。投影方向は、初期値でベクターを指定できる。図は[Vector 2Pt]コンポーネントで作成したベクトル方向に投影した例。
Pull Curve*
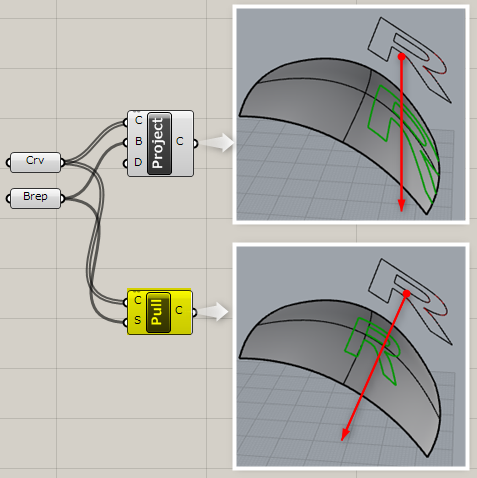
A


Curve>Util
入力したサーフェス(Surface)に最も近づくように、指定した曲線(Curve)をサーフェス上に投影する。
詳細1:[Project]コンポーネントと同様にカーブを投影するが、[Pull Curve]コンポーネントは、ベクターを指定しなくても対象のサーフェスの曲率を見て、法線方向に合わせるように投影する。
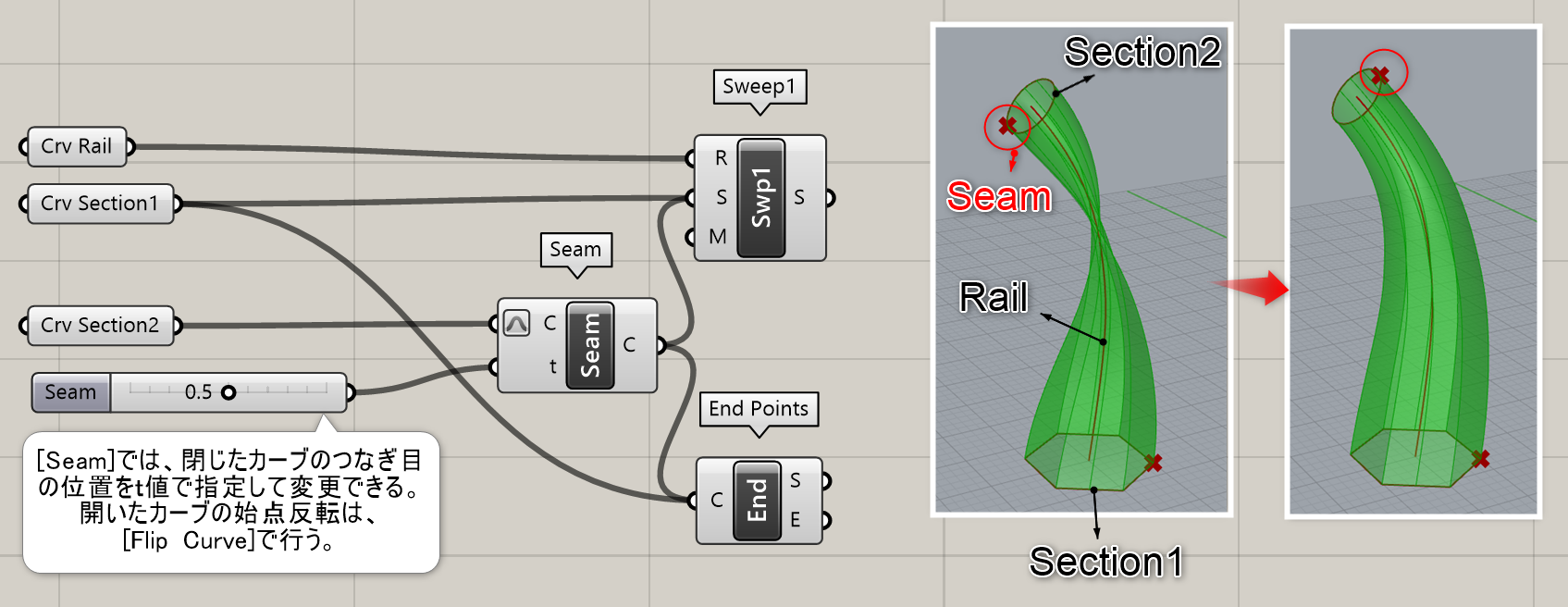
Seam*
B


Curve>Util
曲線(Curve)とtパラメータを入力し、指定した位置が始点となる曲線を作成する。Sweepコンポーネントなどで、断面曲線のSeamを繋ぎ合わせる位置に変更するために使用する。
詳細1:閉じた曲線(Curve)とtパラメータを入力し、t値がつなぎ目となる曲線を作成する。図は、[Sweep1]でSection(断面)2のt値を変更してSweepのねじれを修正した例。
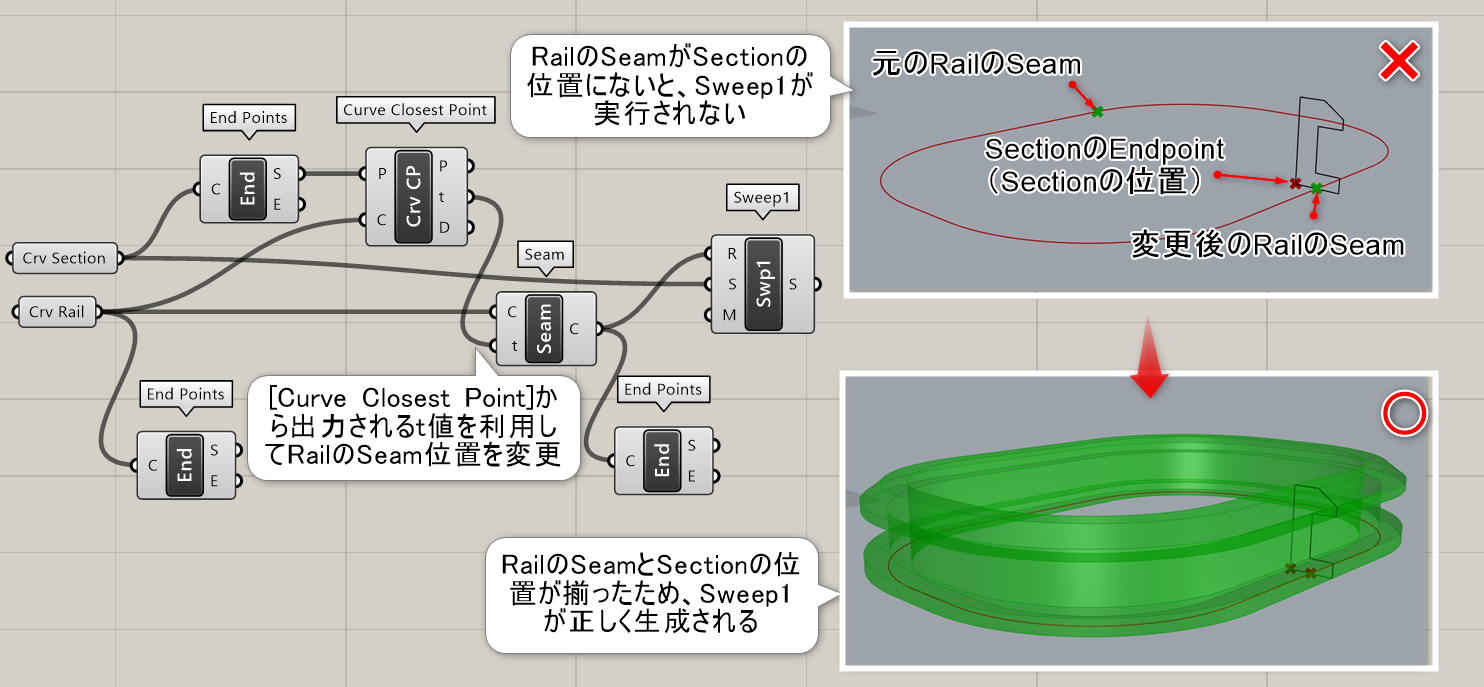
詳細2:閉じたRail曲線に対するSweepの場合、RailのSeamとSectionの位置が合っている必要がある。図は、RailのSeamを[Curve Closest Point]のt値を利用して、Sectionの位置に揃えた例。
Curve To Polyline
C
Curve>Util
曲線(Curve)を入力し、ポリライン(Polyline)に変換する。指定できるオプションは、曲線との距離(Tolerance Distance)、角度(Tolerance Angle)、作成されるポリラインの長さの最小値(MinEdge)、最大値(MaxEdge)。
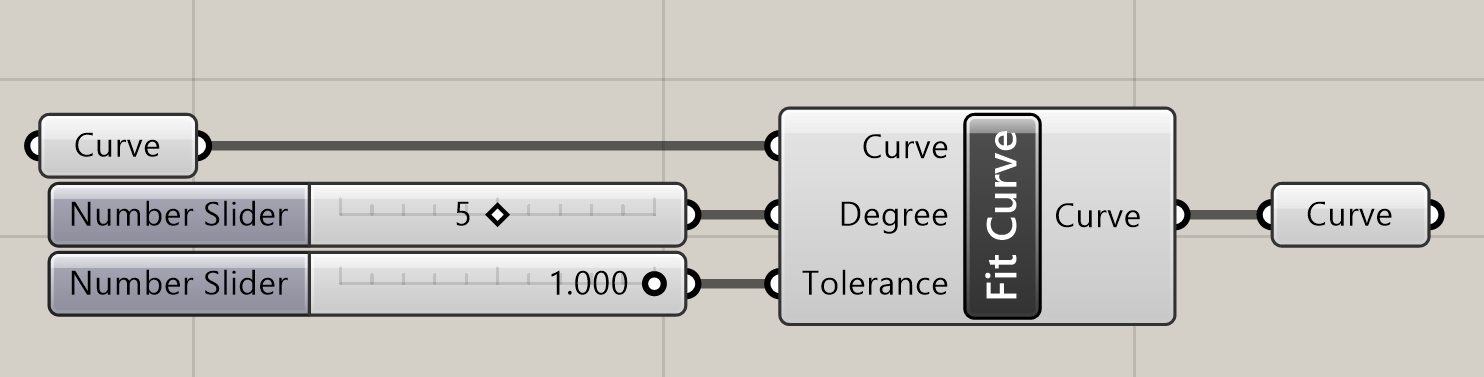
Fit Curve*
A


Curve>Util
曲線(Curve)と次数(Degree)、許容差(Tolerance)を指定し、制御点の数を減らした曲線(Curve)を作成する。
詳細1:指定した次数と許容差によって入力した曲線に近似した曲線を作成する。

Polyline Collapse
C

Curve>Util
ポリライン(Polyline)と許容差(Tolerance)を入力し、指定した値以下の長さの線分を削除する。削除した線の中点につなぎ直す形になる。
Rebuild Curve*
A
Curve>Util
曲線(Curve)と次数(Degree)、制御点の数(Count)を指定し、曲線を作り直す。オプションで、端点の接線方向を維持するかどうかをTrue・Falseで指定できる。
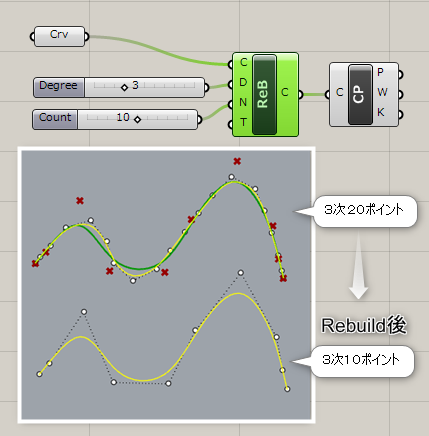
詳細1:カーブを”Rebuild(再構築)”する。
入力Dに次数(初期値は”3″)、入力Nに制御点数(初期値は”10″)を指定。
Reduce
C

Curve>Util
ポリライン(Polyline)と許容差(Tolerance)を入力し、許容差以内で不要な頂点を削除する。
Simplify Curve
C

Curve>Util
曲線(Curve)と許容差(Tolerance)、角度許容差(Angle)を指定し、直線や円弧を単純化した曲線(Curve)を出力する。Rhinoで言うSimplifyCrvのような働き。
Smooth Polyline
C
Curve>Util
ポリライン(PolyLine)を入力し、滑らかなポリラインに変更する。一回当たりの滑らかにする強さ(Strength)とその回数(Times)を指定できる。