- グループ名ボタンをクリックで各グループ一覧にジャンプします。
- 左にあるA～Cは重要度で、Aが一番重要度の高いコンポーネントになります。
- 「詳しい機能を見る」をクリックで詳細説明が開きます。
Goals-6dof
AlignFaces
B
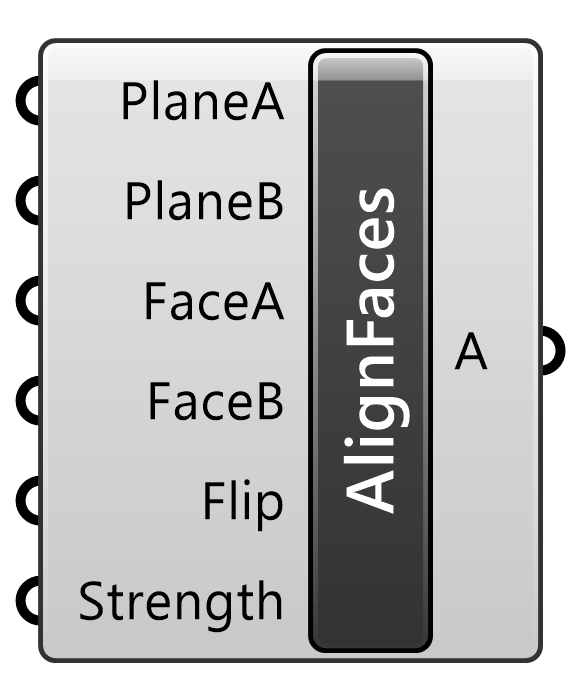
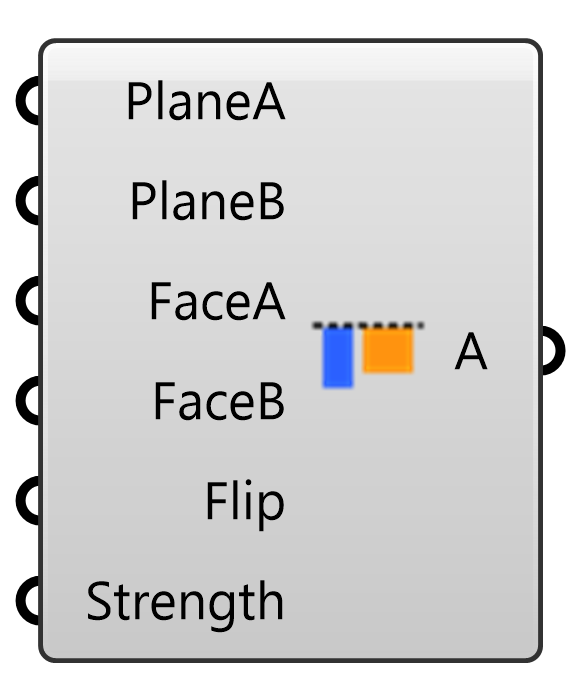
Kangaroo2＞Goals-6dof
入力された2つの剛体（PlaneA／PlaneB）上にそれぞれ定義された面（FaceA／FaceB）が一致するように変形するゴールオブジェクト。Solverに接続して用いる。
Beam
B
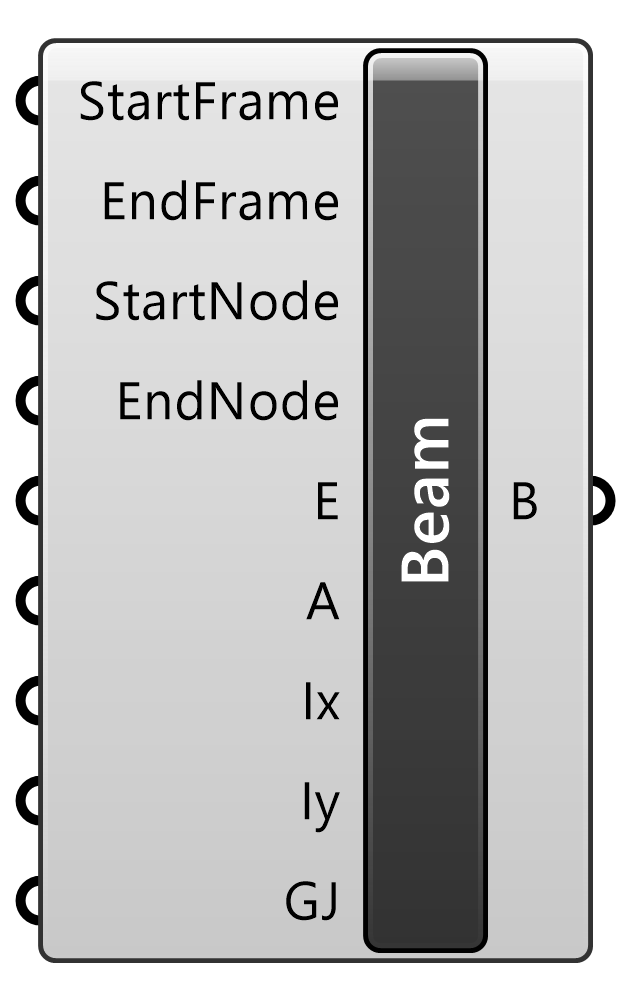
Kangaroo2＞Goals-6dof
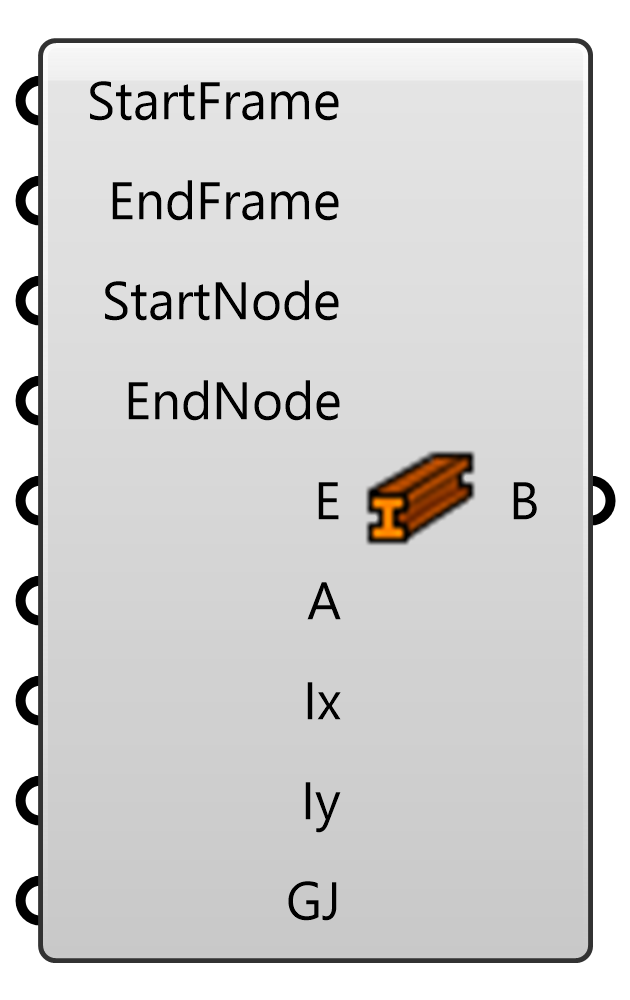
梁を定義するゴールオブジェクト。軸の方向が必要なため、梁の端点（Frame）にはPlaneを入力する。StartFrameのZ軸方向が梁の要素座標系のz軸方向となる。ヤング率（E）、断面積（A)、断面2次モーメント（Ix／Iy）、剛性率とねじり係数の積（GJ）が設定可能。Solverに接続して用いる。
Concentric
B
Kangaroo2＞Goals-6dof
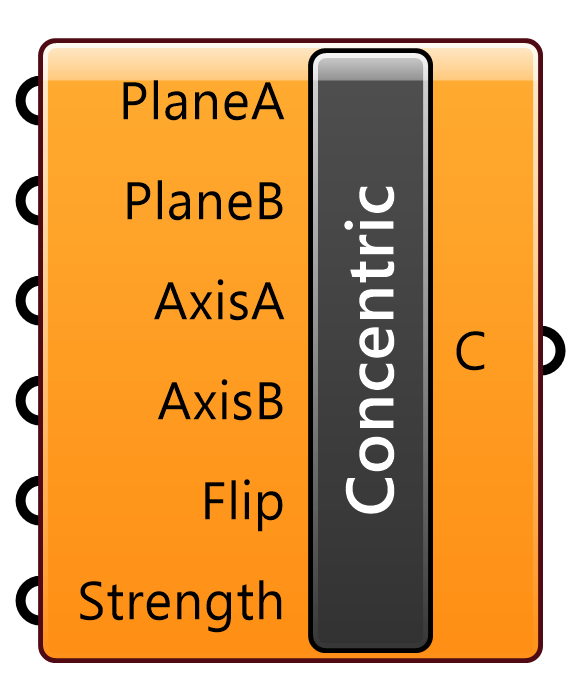
入力された2つの剛体（PlaneA／PlaneB）上にそれぞれ定義された軸（AixsA／AxisB）が一致するように変形するゴールオブジェクト。Solverに接続して用いる。
RigidBody
A
Kangaroo2＞Goals-6dof
入力されたオブジェクト（Part）を剛体として設定するゴールオブジェクト。球体以外のソリッドの衝突を扱いたい場合に用いる。複数の剛体同士の衝突をシミュレートしたい場合はそれぞれの座標系（Plane）を統一させておく必要がある。オプションの点（Points）を剛体に対して定義すれば、Grabなどで点として認識させることができる。Solverに接続して用いる。
サンプルデータをダウンロードできます 
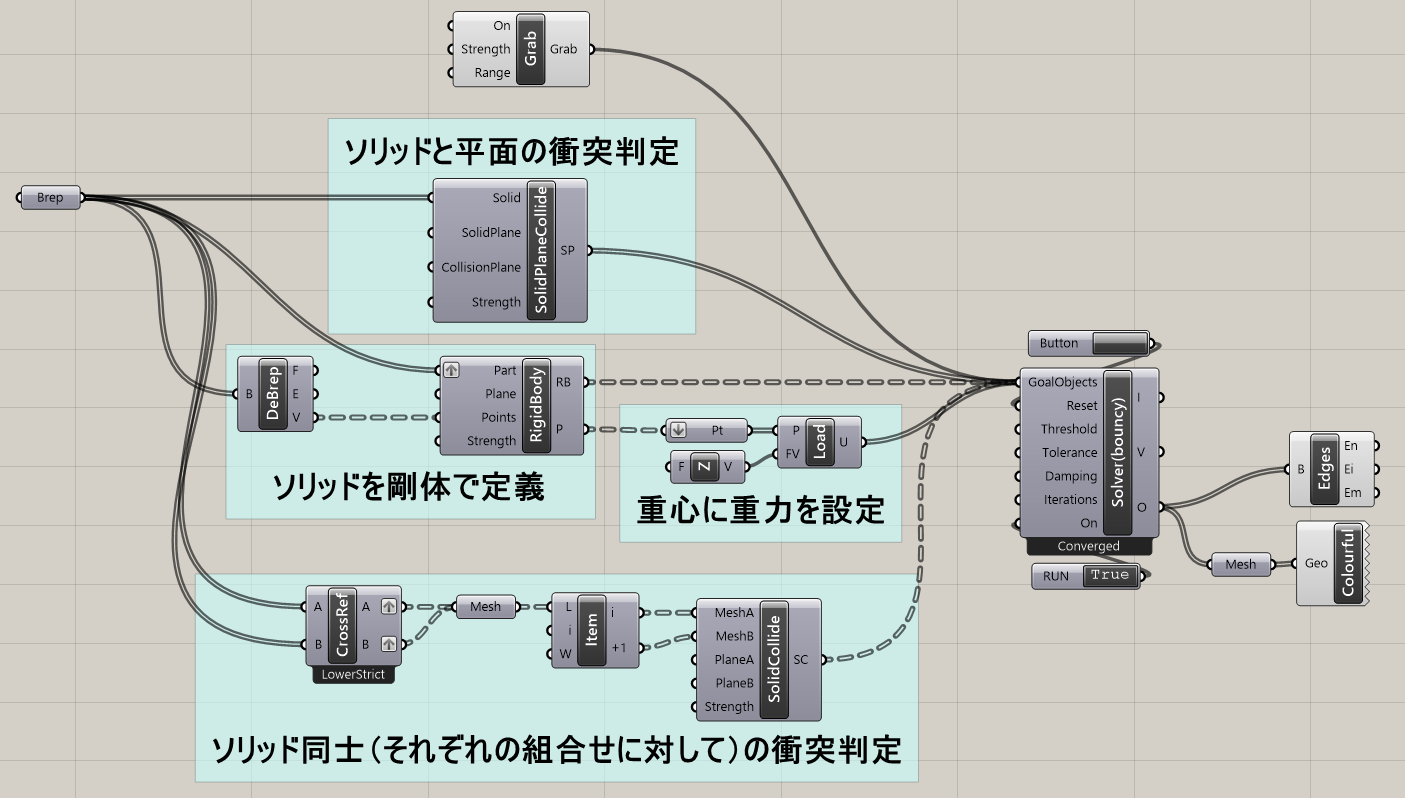
詳細1：図は複数の直方体ソリッドを剛体（RigidBody）として定義し、まとめて作業平面上に落下させた例とそのアルゴリズムだ。
[RigidBody]ゴールオブジェクトを通すことで、それぞれ剛体（変形しない大きさのある物体）として認識されているので、ぶつかっても互いに食い込まないように計算されている（これに対し、[SolidPointCollide]・[SphereCollide]は、「ソリッドと質点」・「球体と球体」同士の衝突判定を設定するゴールオブジェクトである）。
直方体の各頂点がPointsに入力されているので、Grabで掴んでマウスで動かすことも可能。
RigidPointSet
B
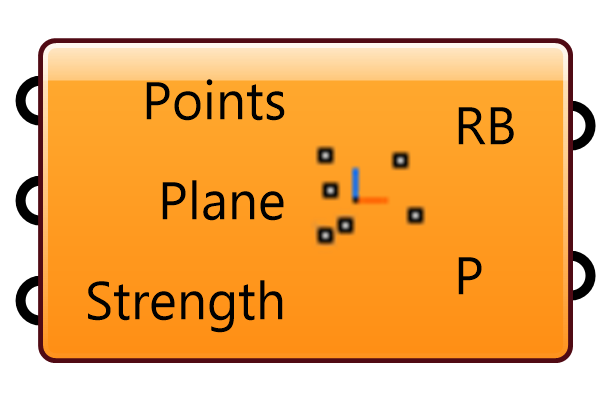
Kangaroo2＞Goals-6dof
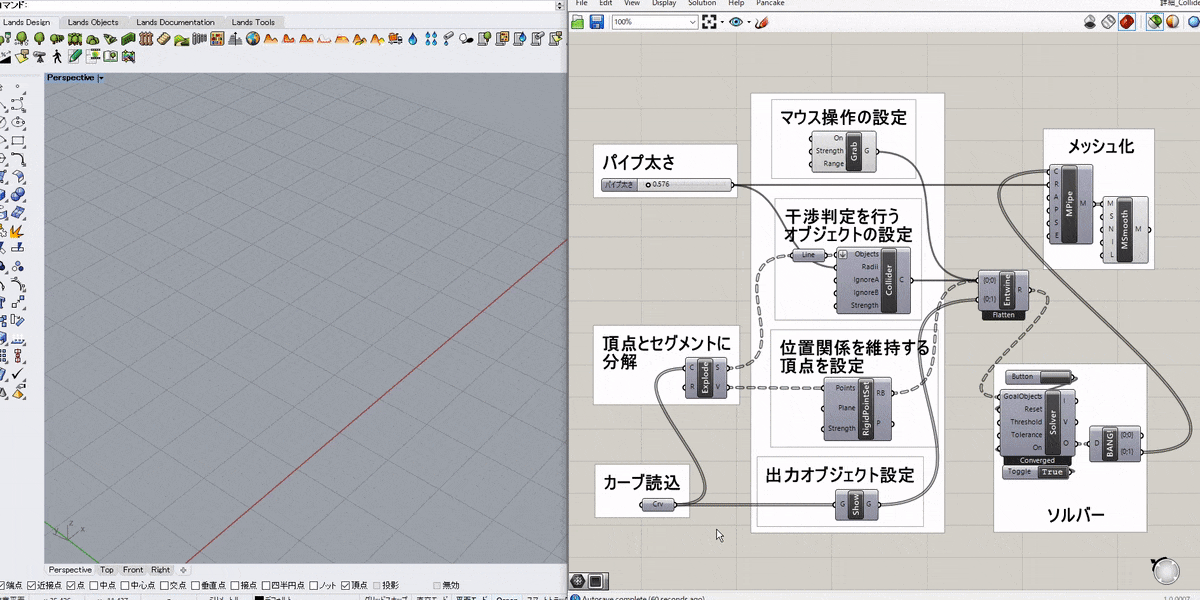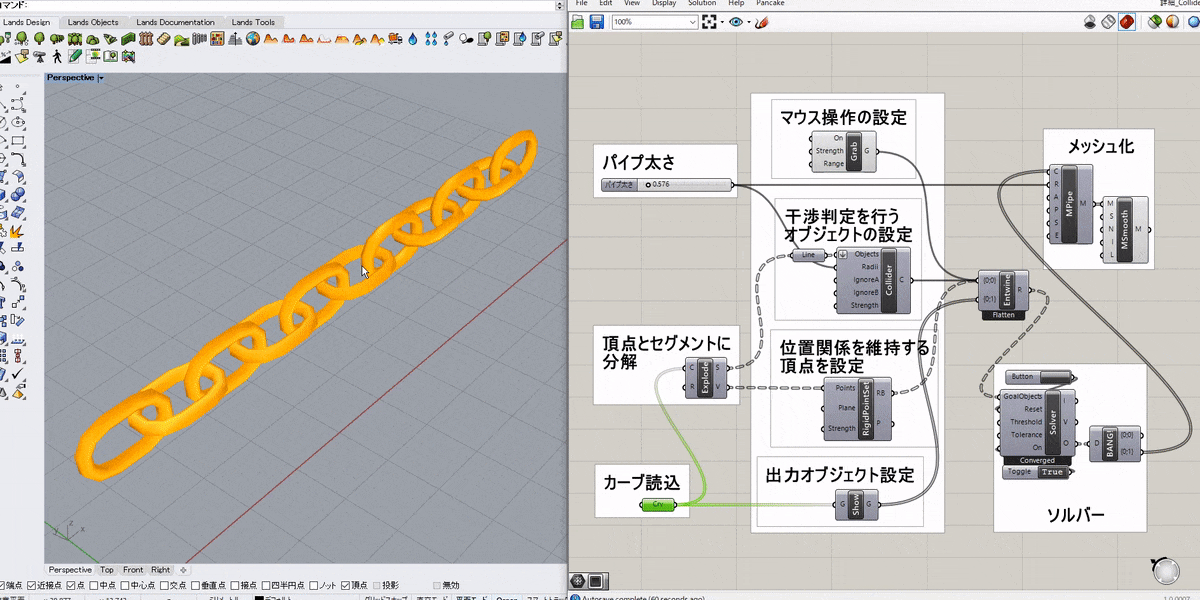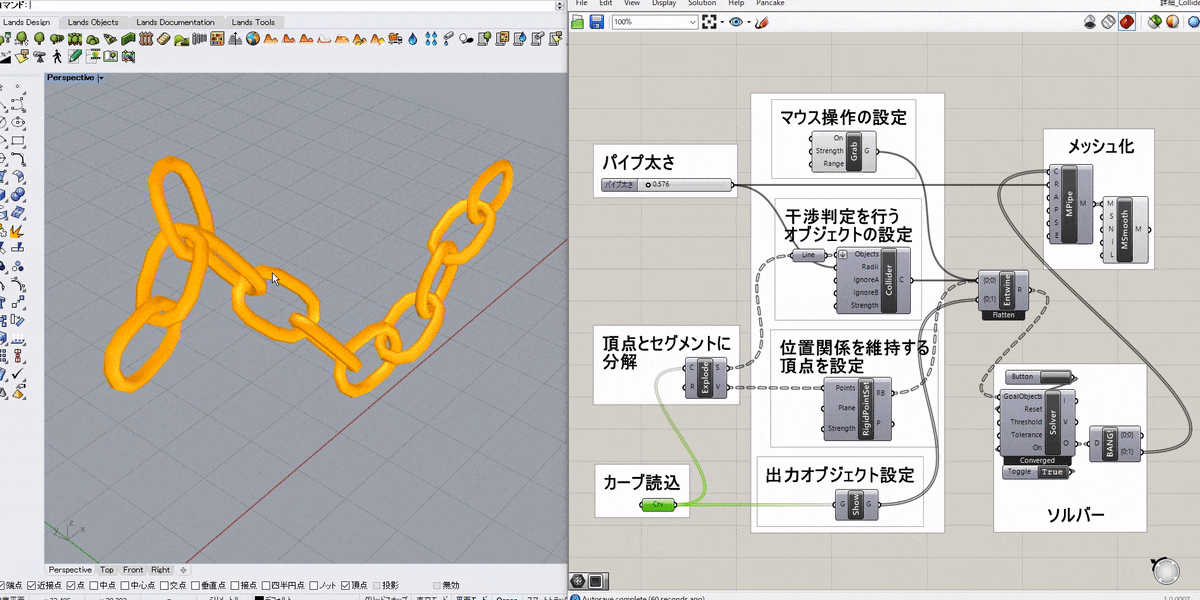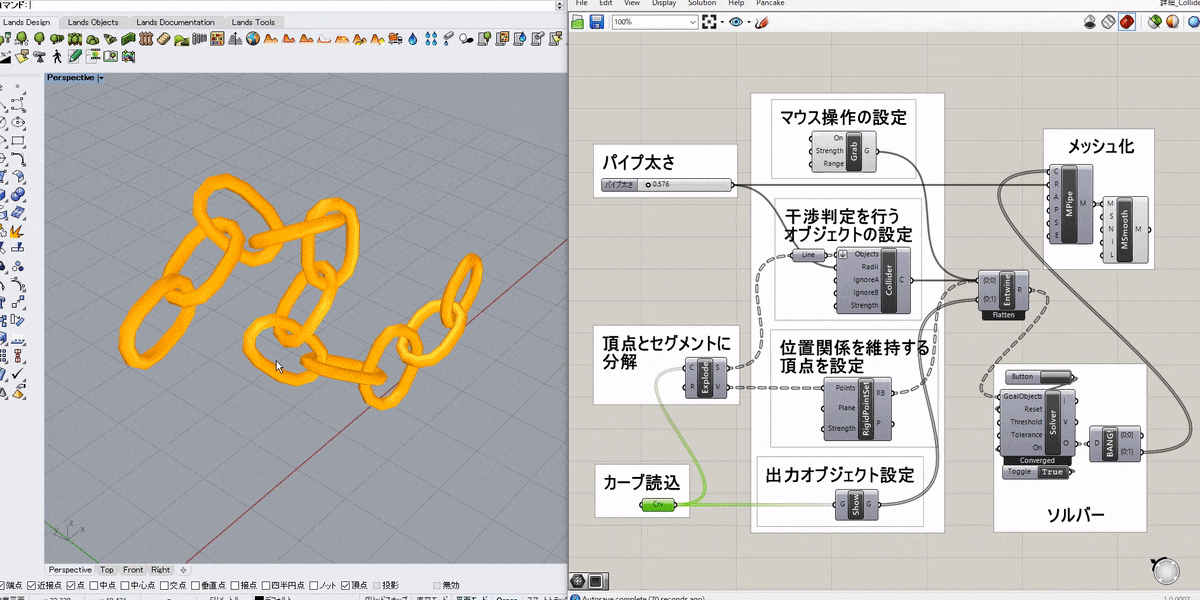
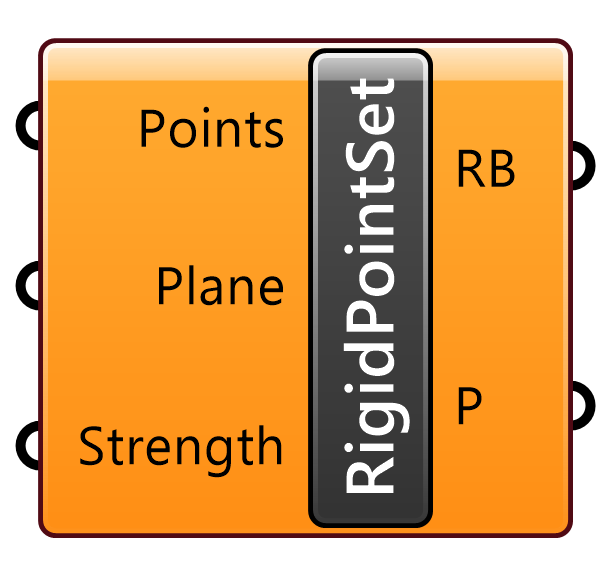
入力した点（Points）同士の相対的な位置関係を拘束するゴールオブジェクト。Solverに接続して用いる。
SolidCollide
B
Kangaroo2＞Goals-6dof
入力されたソリッド同士（MeshAとMeshBのペア）の衝突判定を設定するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細1：図は複数の直方体ソリッドを剛体（RigidBody）として定義し、まとめて作業平面上に落下させた例とそのアルゴリズムだ。
[SolidCollide]ゴールオブジェクトを用いて、MeshAとMeshBに入力されたソリッド同士の衝突を判定する。3つ以上の物体を用いる場合は、それぞれの組み合わせを用いる必要があるので、[CrossReference]コンポーネントを利用し、すべての組み合わせのリストを作成してからまとめて入力すると良い。
SolidPlaneCollide
B
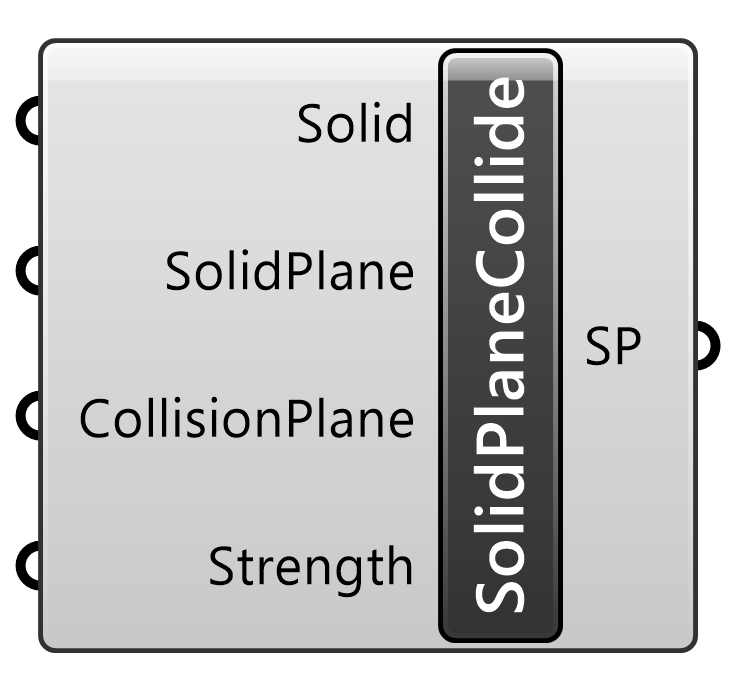
Kangaroo2＞Goals-6dof
入力されたソリッド（Solid）と平面（CollisionPlane）との衝突判定を設定するゴールオブジェクト。衝突平面はデフォルトではWorldXY平面となる。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細1：図は、RigidBodyで設定したオブジェクトに重力方向の荷重を掛け、床との衝突判定により、床に置いたときのバランスを確認した例である。
詳細2：図は複数の直方体ソリッドを剛体（RigidBody）として定義し、まとめて作業平面上に落下させた例とそのアルゴリズムだ。
[SolidPlaneCollide]ゴールオブジェクトを用いて、SolidとCollisionPlaneに入力されたソリッドと平面の衝突を判定する。CollisionPlaneは、デフォルトでは「World XY」となるので何も入力しない場合は、XY平面が衝突判定用の平面となる。
Support
B
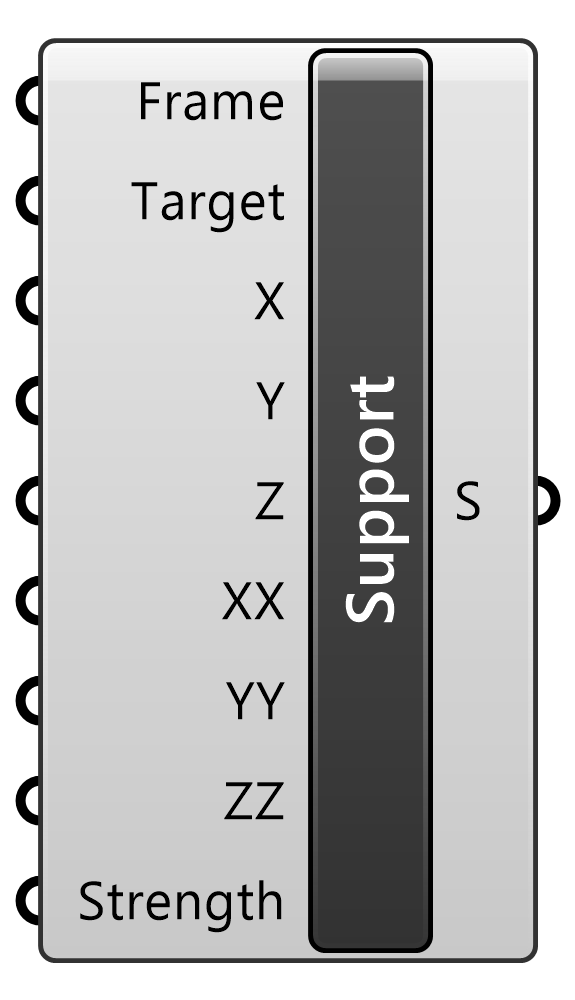
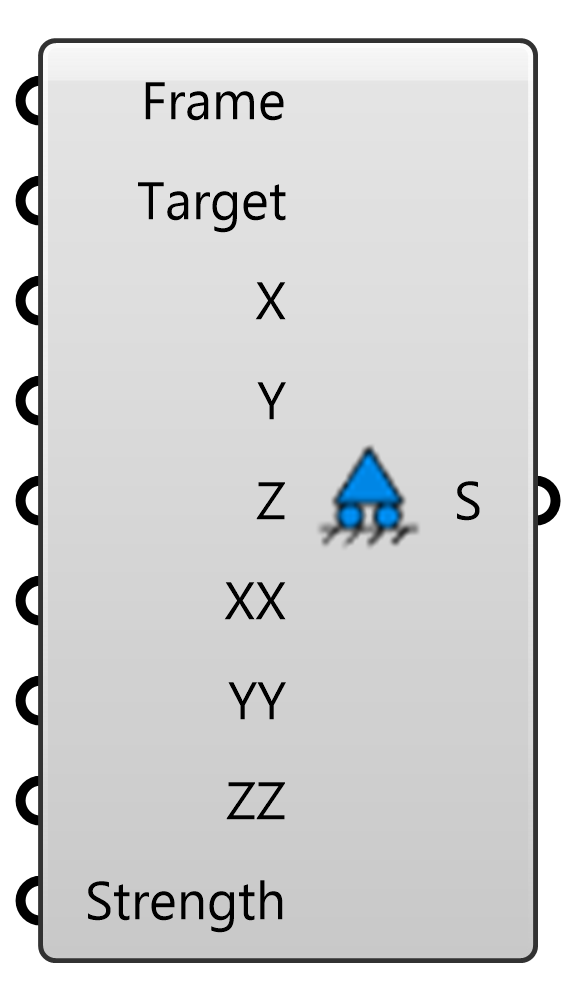
Kangaroo2＞Goals-6dof
梁の端点や剛体に拘束条件を与えるゴールオブジェクト。方向が必要になるため、点ではなく、平面（Frame）を入力として用いる。6自由度の入力に対して論理値（True／False）で拘束条件を指定する。Solverに接続して用いる。
Goals-Angle
Angle
A
Kangaroo2＞Goals-Angle
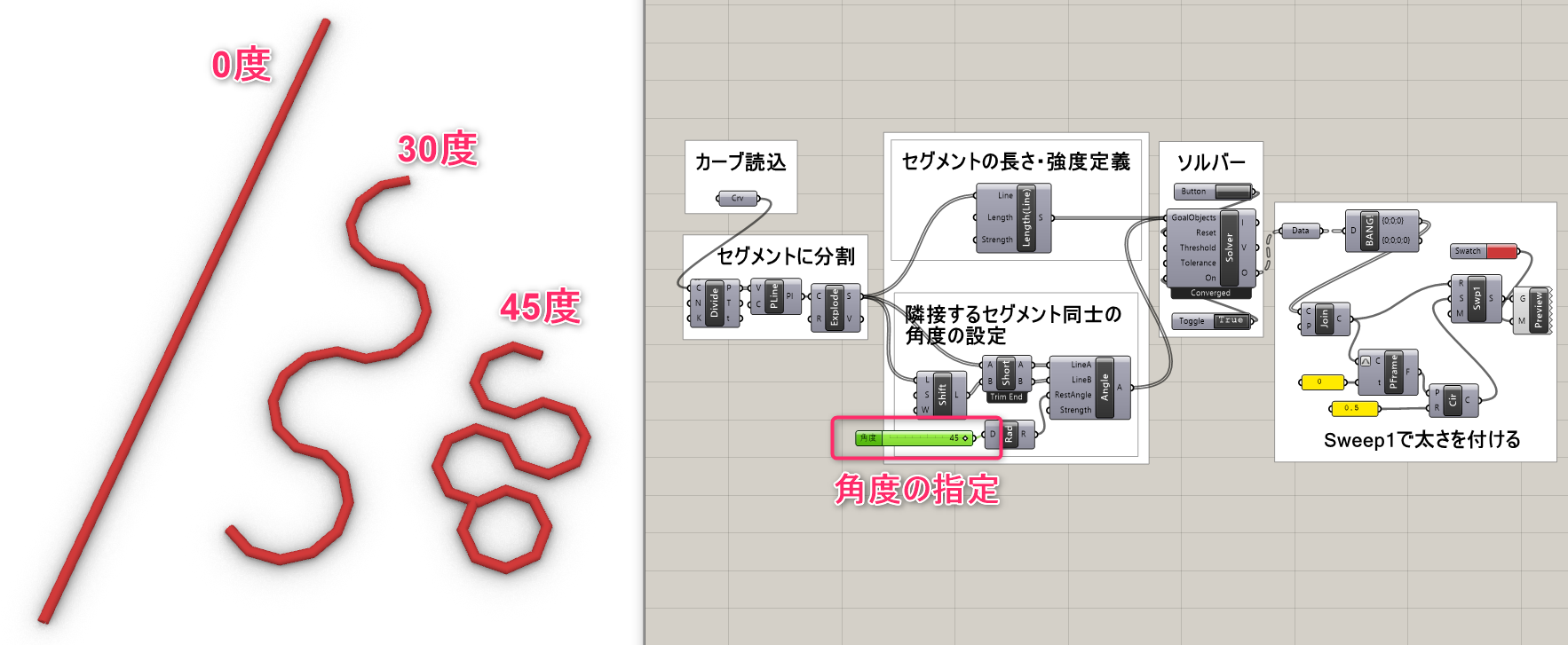
2つの直線の角度を指定した値（RestAngle）に変形するゴールオブジェクト。角度はラジアンで指定する。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細１：なめらかな曲線を線分に分割し、隣り合う線分同士の角度を指定して変形した例。
ソルバーのToggleをTrueにすると計算が開始される。
詳細2：それぞれ、角度を0度／30度／45度にした場合。0度にするとロープを引き伸ばしたような形状をシミュレートできる。
どちらの方向に折れ曲がるかはその時の形状によって変わる。
AngleSnap
C
Kangaroo2＞Goals-Angle
入力した直線（Line）間の角度を指定された角度（Factor）の整数倍に制限するゴールオブジェクト。例えばFactorを15°とするとLineAとLineBの角度は、15°、30°、45°など15°の倍数で制限される。角度(Factor）はラジアンで入力する。Solverに接続して用いる。
ClampAngle
C
Kangaroo2＞Goals-Angle
入力された曲線（Line）間の角度が境界条件（LowerLimit～UpperLimit）内に収まるように制限するゴールオブジェクト。角度はラジアンで入力する。Solverに接続して用いる。
EqualAngle
C
Kangaroo2＞Goals-Angle
入力された曲線（Line）間の角度がすべて等しくなるように変形するゴールオブジェクト。Solverに接続して用いる。角度はすべて平均値に等しくなる。
G2
B
Kangaroo2＞Goals-Angle
入力された点（Points）の制御点から成るNURBS曲線の曲線連続（G2連続）を維持するゴールオブジェクト。Solverに接続して用いる。
Rod
B
Kangaroo2＞Goals-Angle
入力したポリライン（Polyline）を元の長さや角度に対する倍数（LengthFactor／AngleFactor）を指定して変形するゴールオブジェクト。Solverに接続して用いる。
Goals-Co
CoCircular
C
Kangaroo2＞Goals-Co
入力された点（Points）を同一円上に維持するゴールオブジェクト。Solverに接続して用いる。
CoLinear
C
Kangaroo2＞Goals-Co
入力された点（Points）を同一直線上に維持するゴールオブジェクト。Solverに接続して用いる。
CoPlanar
B
Kangaroo2＞Goals-Co
入力された点（Points）を同一平面（共面）上に維持するゴールオブジェクト。Solverに接続して用いる。
CoSpherical
C
Kangaroo2＞Goals-Co
入力された点（Points）を同一球上に維持するゴールオブジェクト。Solverに接続して用いる。
Goals-Col
Collider
A
Kangaroo2＞Goals-Col
入力オブジェクト（Objects）同士の衝突判定を設定するゴールオブジェクト。接触半径（Radii）や強さ（Strength）を設定することで衝突時の反発・すり抜けの度合いを調整する。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細１：線分、または点同士の干渉を判定する。以下は、輪状のカーブを複数用意し、鎖のような動きをシミュレートした例。
ソルバーのToggleをTrueにすると計算が開始される。
それぞれのコンポーネントは以下のような役割となっている。
[Collider] → 干渉・衝突判定
[RigidPointSet] → 輪っかの形状を維持
[Grab] → マウスで変形できるように
[Show] → ソルバーから個別に出力されるオブジェクトを設定
CurveCollide
C
Kangaroo2＞Goals-Col
入力された閉じた曲線同士の衝突判定を設定するゴールオブジェクト。Grab等で動かせる曲線（C）と衝突があっても動かない曲線（P）を分けて設定できる。デフォルトではworldXY平面を基準に衝突が判定される。Solverに接続して用いる。
CurvePointCollide
B
Kangaroo2＞Goals-Col
入力された点（Points）が常に平面上の曲線（Curve）の内側にあるか外側にあるかを指定し、衝突判定を設定するゴールオブジェクト。平面はデフォルトではWorldXY平面となる。Solverに接続して用いる。
ImageCircles
B
Kangaroo2＞Goals-Col
画像のカラーに応じたサイズの異なる円の衝突をシミュレート（Circle Packing）するゴールオブジェクト。最小サイズ（Min）と最大サイズ（Max）を指定でき、色の暗い部分ほど小さい円となる。Solverに接続して用いる。
SolidPointCollide
A
Kangaroo2＞Goals-Col
入力された点（Points）がソリッドメッシュ（Solid）に対して、内側にあるか外側にあるかを指定し、衝突判定を設定するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
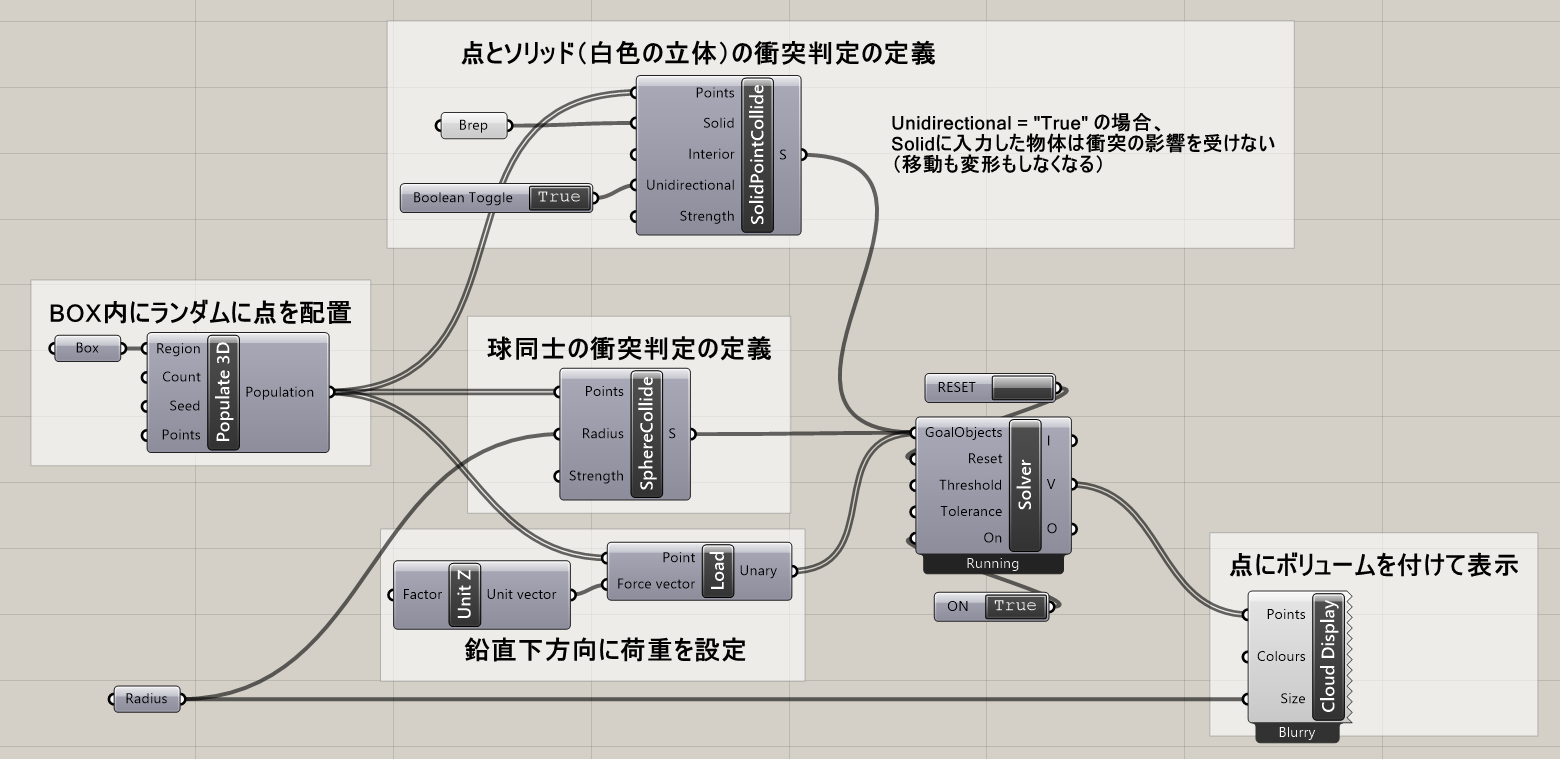
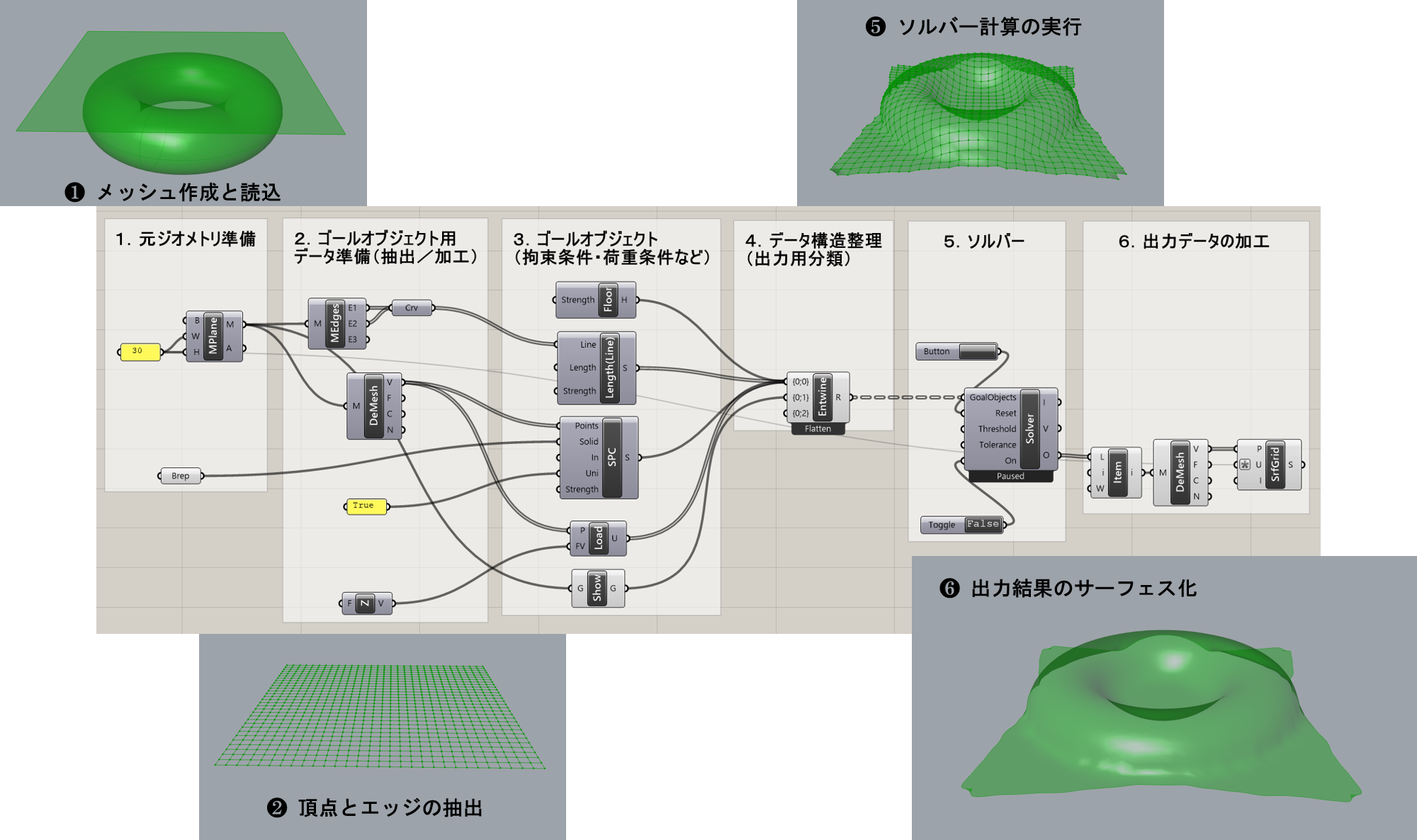
詳細1：図1・図2は、多数の球（点）を器状のソリッドに落下させた例とそのアルゴリズムだ。[SolidPointCollide]ゴールオブジェクトを用いることで、点とソリッドの衝突判定が設定でき、互いにぶつかったときにすり抜けないようになる。
Unidirectionalは、デフォルトは「False」で、「Ture」にするとソリッドは衝突の影響を受けず、動きも変形もしない状態となる（この場合「False」にすると器の底に穴が空き、球はすべて下に落ちていく）。
Interiorはデフォルトは「False」で、「True]にすると点はソリッド内部に閉じ込められた状態を維持する。
[SolidCollide]との違いは、[SolidCollide]はソリッドとソリッドの衝突判定であるのに対し、[SolidPointCollide]は点とソリッドの衝突判定であるため、そのまま点を球としてプレビューすると図3のように球がソリッドに食い込んだような表示となる。また、球と球の衝突は、[SphereCollide]で判定している。
詳細2：バラバラの点ではなく、メッシュの頂点とソリッドの衝突判定にも用いられる。
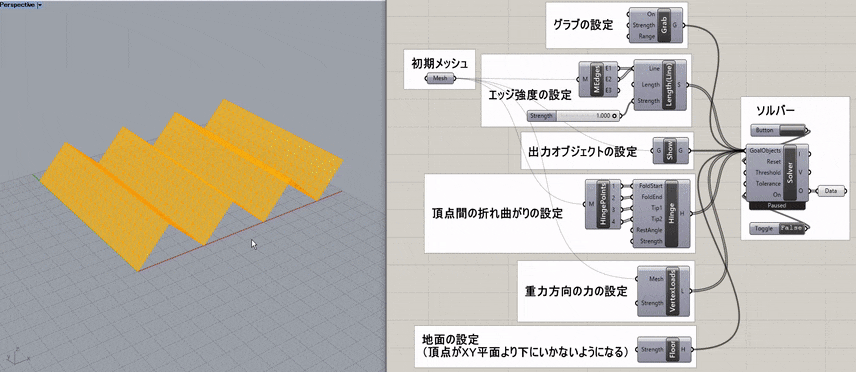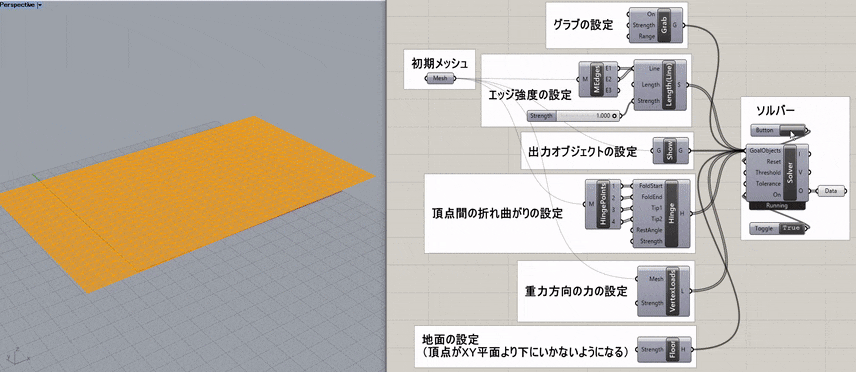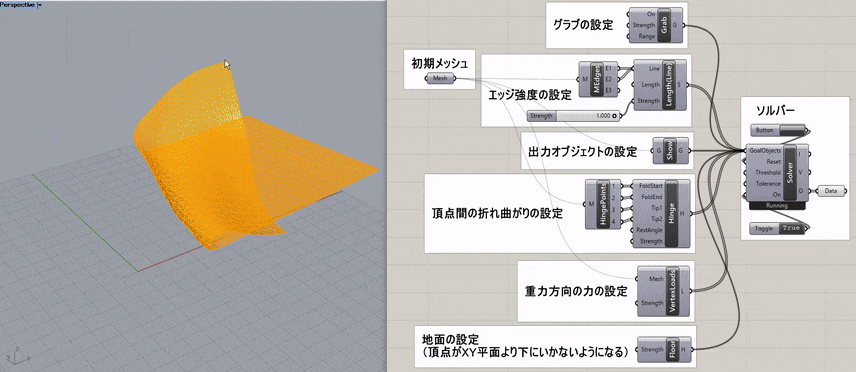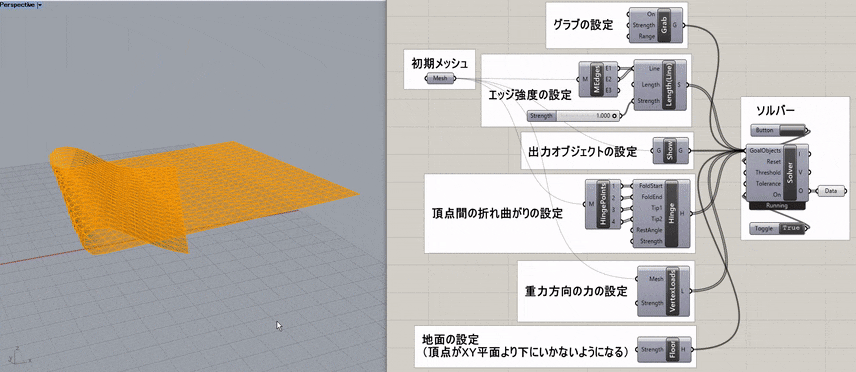
下図は、ドーナツ型の立体に布を覆いかぶせたような形状を作成する過程（Drape）をシミュレートした例だ。
各頂点とソリッドの衝突判定により、点がソリッドをすり抜けないようになっており、[Length(Line)]と組み合わせることで点同士の位置関係（エッジ）も維持されている。
ただし、この方法は摩擦は考慮されていないので長時間演算を続けるとだんだんと平衡が保てず、布がずり落ちてくることがあるのである程度演算が進んだら、
途中でソルバーをOFFにして計算を止めると良い。
SphereCollide
A
Kangaroo2＞Goals-Col
複数の同一サイズの球の衝突をシミュレートするゴールオブジェクト。複数の球の中心点（Points）と半径（R）を入力する。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細1：最もシンプルな使い方は、球同士の衝突判定をシミュレートする方法だ。Pointに入力した点を中心として、Radiusで設定した大きさの球同士の衝突を判定する。
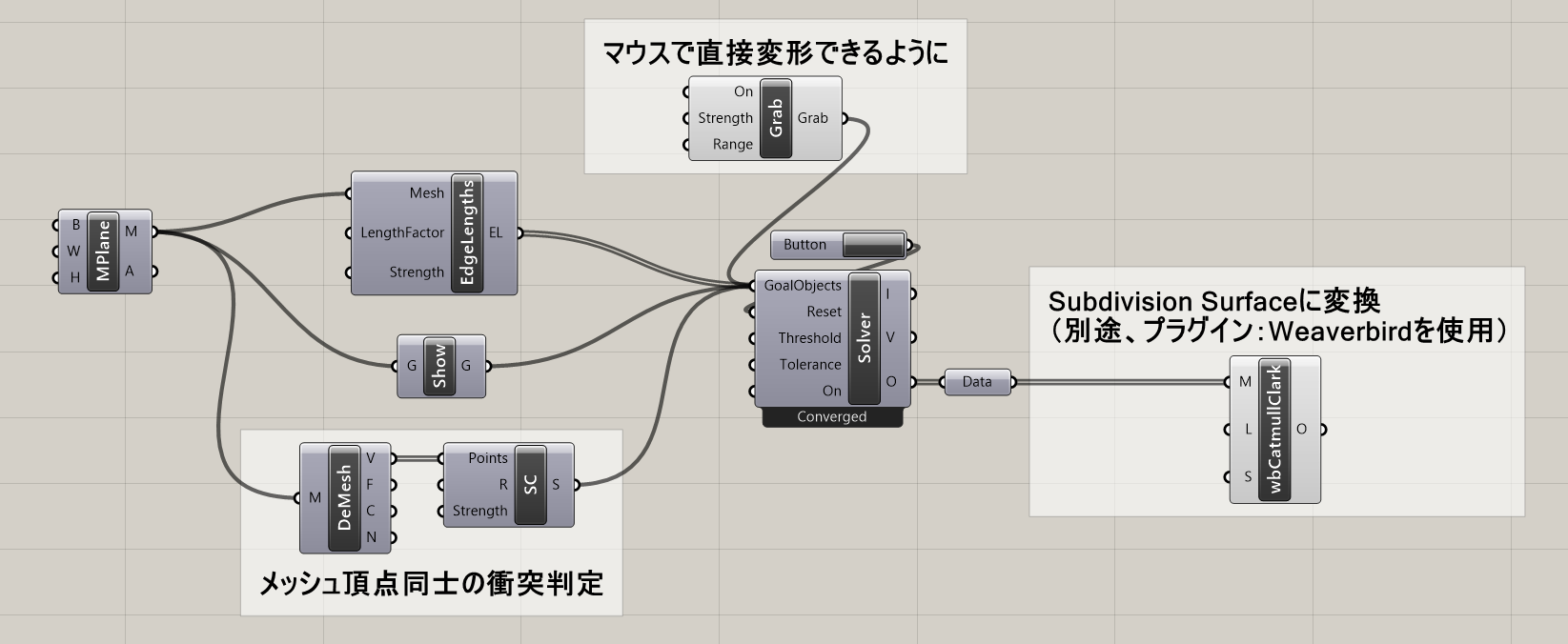
詳細2：SphereCollideという名称ではあるが、球としてではなく、メッシュの各頂点同士の干渉判定にも用いられる。
図3・図4は、平面メッシュの頂点をGrabで移動し布のように変形させた例とそのアルゴリズムだ（別途、プラグイン「Weaverbird」を使用している）。
[SphereCollide]の頂点同士の干渉判定により、エッジがねじれないようになるので、実際の布を変形したような形を維持できている。
Weaverbirdの[Weaverbird’s Catmull–Clark subdivision]コンポーネントを組み合わせることで、綺麗に細分されたQuadメッシュを取り出すことができる（図5）。
Goals-Lin
ClampLength
B
Kangaroo2＞Goals-Lin
入力された曲線（Line）の長さが境界条件（LowerLimit～UpperLimit）内に収まるように制限するゴールオブジェクト。Solverに接続して用いる。
ConstantTension
C
Kangaroo2＞Goals-Lin
入力された直線（Line）の張力が一定となるように直線の硬さを調整するゴールオブジェクト。Solverに接続して用いる。
Direction
C
Kangaroo2＞Goals-Lin
入力された直線（Line）の向きをDirectionで指定した向きに変形するゴールオブジェクト。Directionを指定しない場合は、最も近いWorld座標軸の方向に変形する。Solverに接続して用いる。
DynamicWeight1d
C
Kangaroo2＞Goals-Lin
入力された直線（Line）にその長さに応じたマイナスZ軸方向の荷重を与えるゴールオブジェクト。単位長さあたりの重さ（W）が調整できる。Solverに接続して用いる。
EqualLength
B
Kangaroo2＞Goals-Lin
入力された曲線（Line）の端点同士の距離がすべて等しくなるように変形するゴールオブジェクト。Solverに接続して用いる。距離はすべて平均値に等しくなる。
Length(Line)
A
Kangaroo2＞Goals-Lin
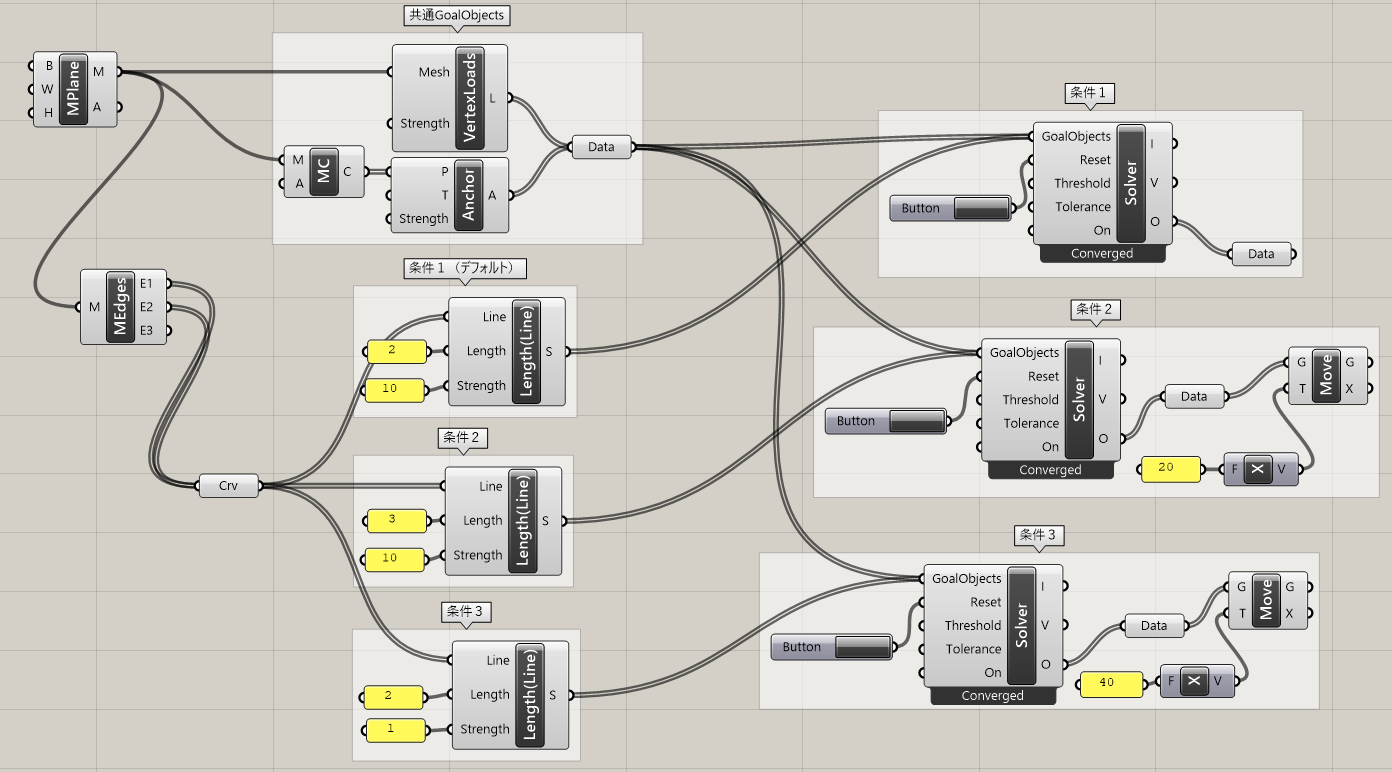
入力された曲線（Line）を指定した長さ（Length）の直線に変形するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細1：[Length(Line)]ゴールオブジェクトの最もシンプルな使い方は、入力した曲線の長さを変形する方法である。直線だけでなく、曲線にも使用できることが特徴。
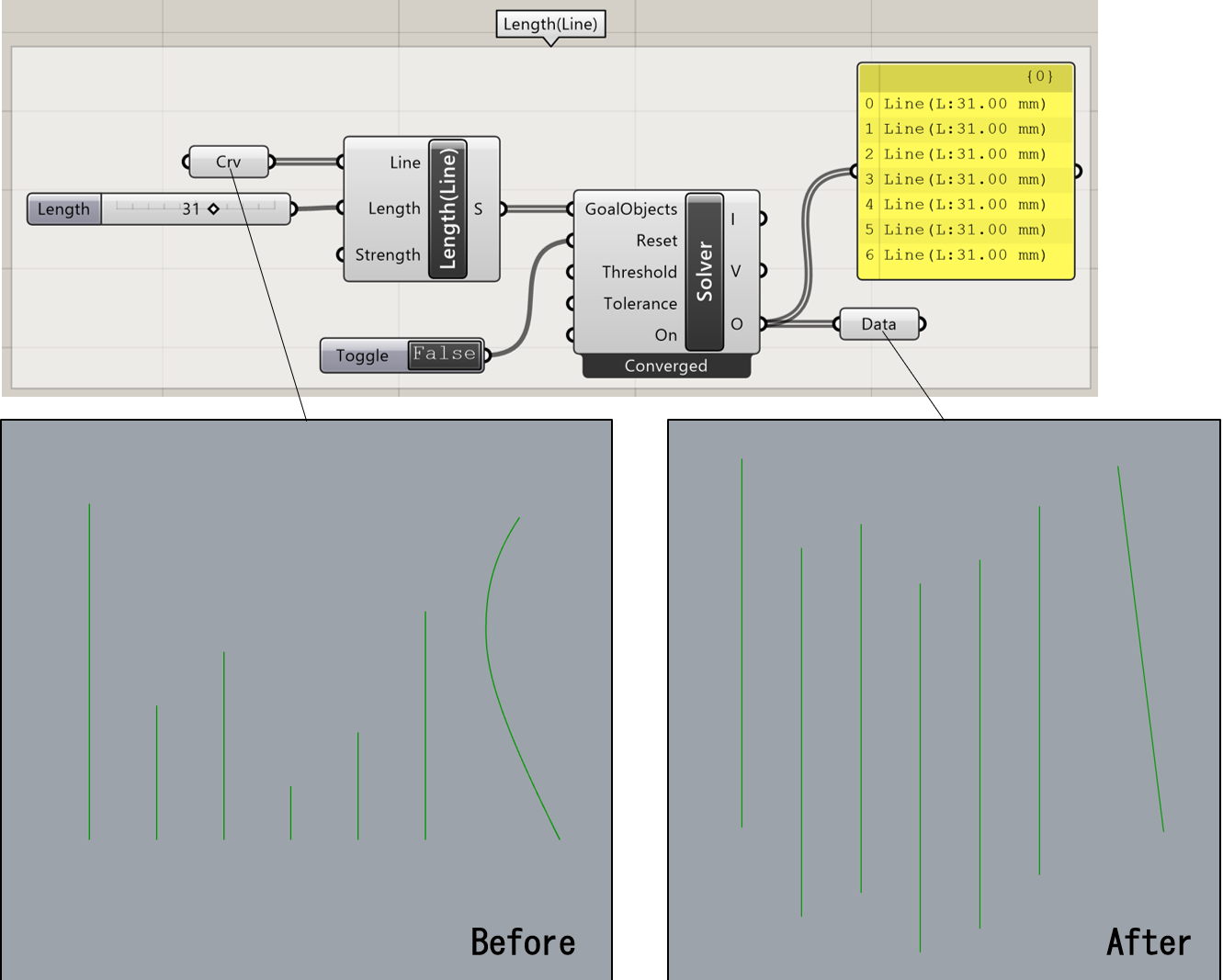
詳細2：実用的には、メッシュのそれぞれのエッジの長さや弾性を定義する際などに多用する。剛体以外を物理演算の対象とする場合は原則、計算前後で長さ(弾性)をどのようにしたいか定義しておく必要があるため、長さを変更せず維持したい場合も同様にこのゴールオブジェクトの設定が必要となる。この定義がない場合、少しでも変形が加わると計算後にエッジ長さが無限小、あるいは無限大となり解が発散してしまう。
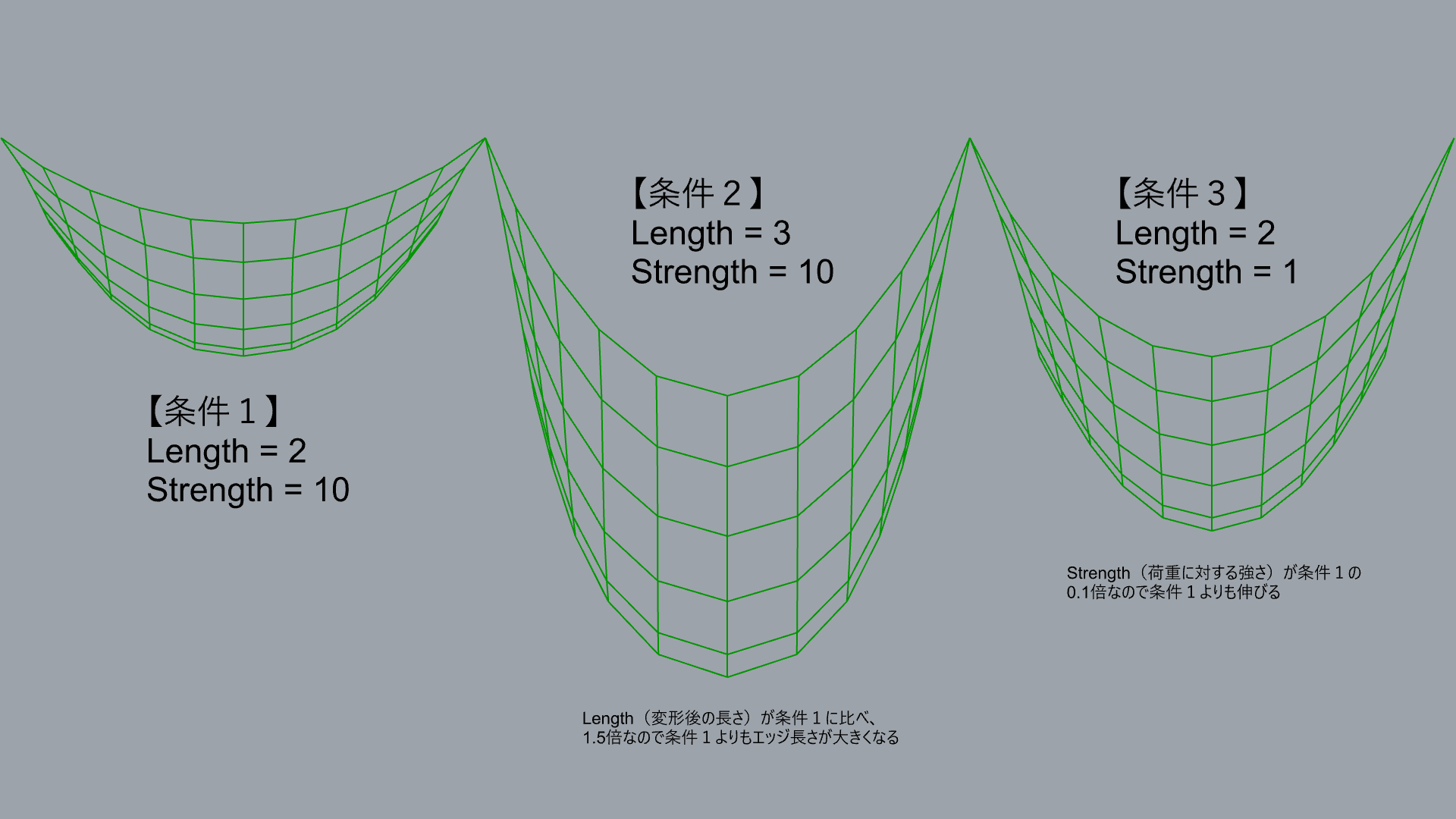
下図はカテナリー変形のシュミレーションの例で、長さや弾性の調整は、Length入力やStrength入力で行う。
LengthRatio
C
Kangaroo2＞Goals-Lin
LineAに対してのLineBの長さ比（Ratio）が入力値に等しくなるように変形するゴールオブジェクト。Solverに接続して用いる。
LengthSnap
C
Kangaroo2＞Goals-Lin
入力した直線（Line）の長さを指定した値（Factor）の整数倍に制限するゴールオブジェクト。Solverに接続して用いる。（注：2019年6月現在うまく動作せず）
PlasticLength
C
Kangaroo2＞Goals-Lin
長さが上限値（L）に達するまでは、入力された直線（Line）を弾性的に変形するよう保持するゴールオブジェクト。Solverに接続して用いる。
Goals-Mesh
Conicalize
C
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）のそれぞれの四角形メッシュが円錐メッシュとなるように頂点を調整するゴールオブジェクト。Solverに接続して用いる。
CyclicQuad
B
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）におけるそれぞれの四角形メッシュの4点から外接円を生成するゴールオブジェクト。Solverに接続して用いる。
Developablize
C
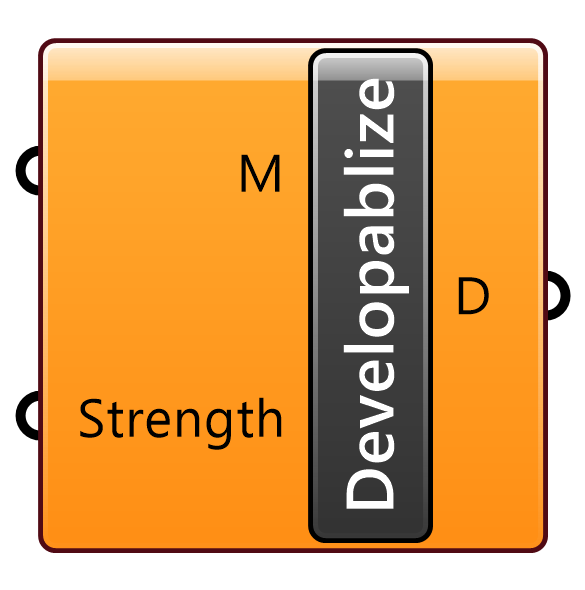
Kangaroo2＞Goals-Mesh
入力された三角形メッシュ（M）を折り目で展開可能なパッチに変換するゴールオブジェクト。
EdgeLengths
A
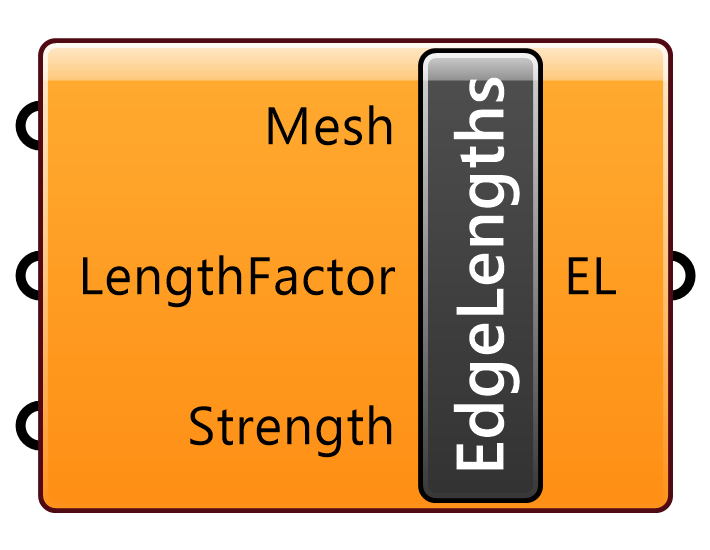
Kangaroo2＞Goals-Mesh
入力されたメッシュ（Mesh）のエッジを抽出するゴールオブジェクト。LengthsFactorに数値を入力するとそれぞれのエッジ長さがその倍数となる。入力しない場合はそのままの長さとなる。Solverに接続して用いる。
サンプルデータをダウンロードできます
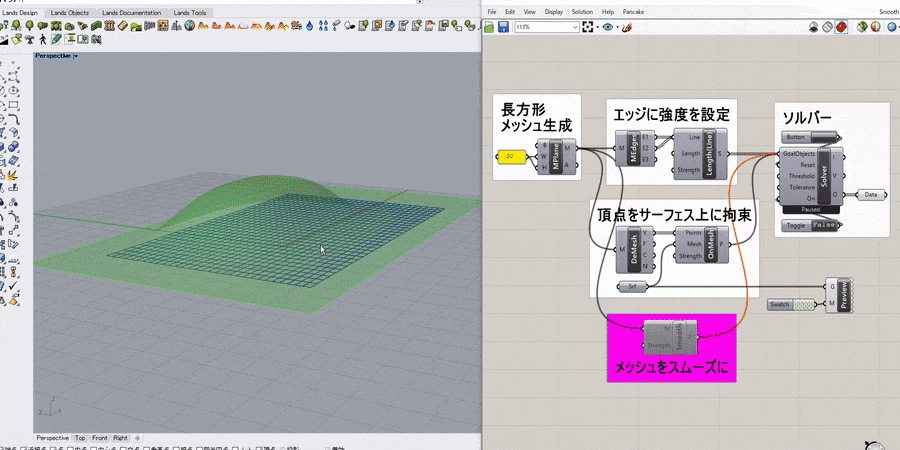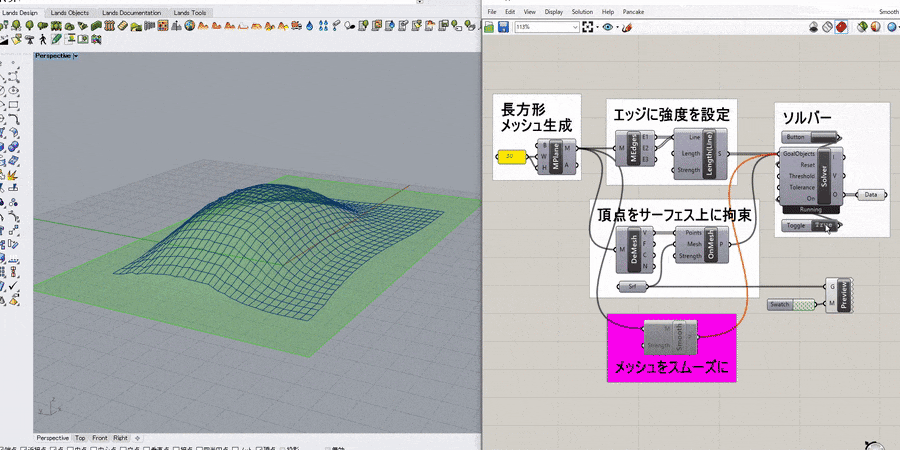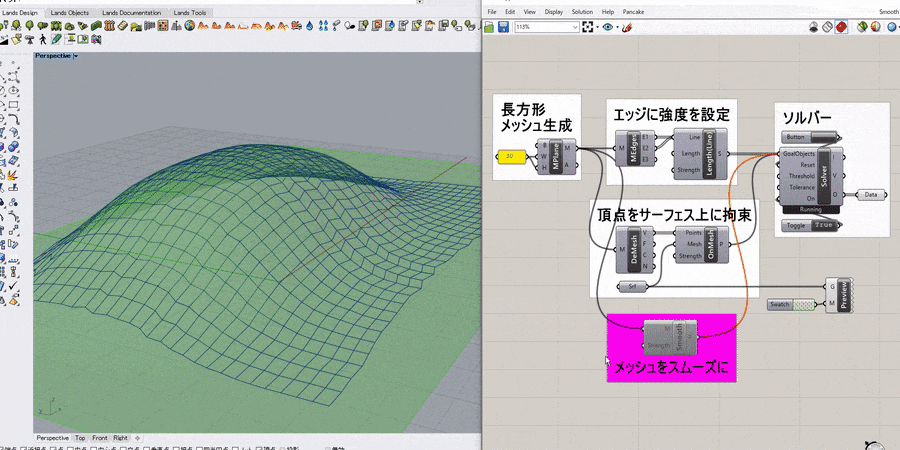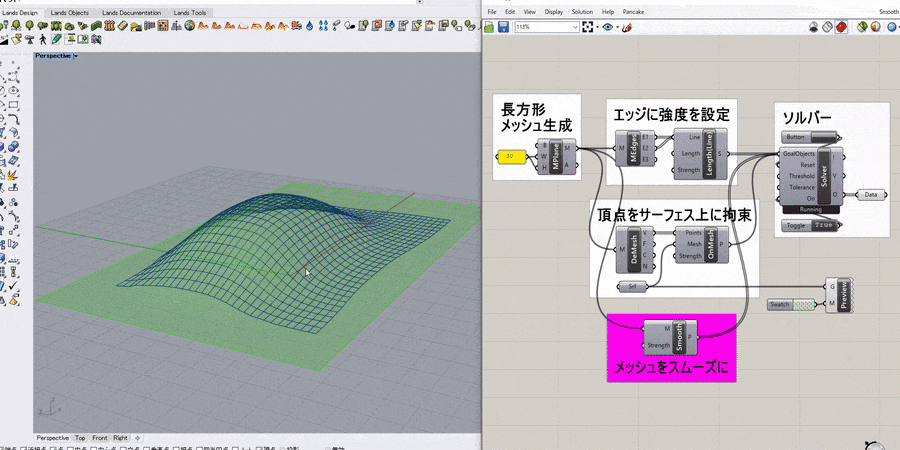
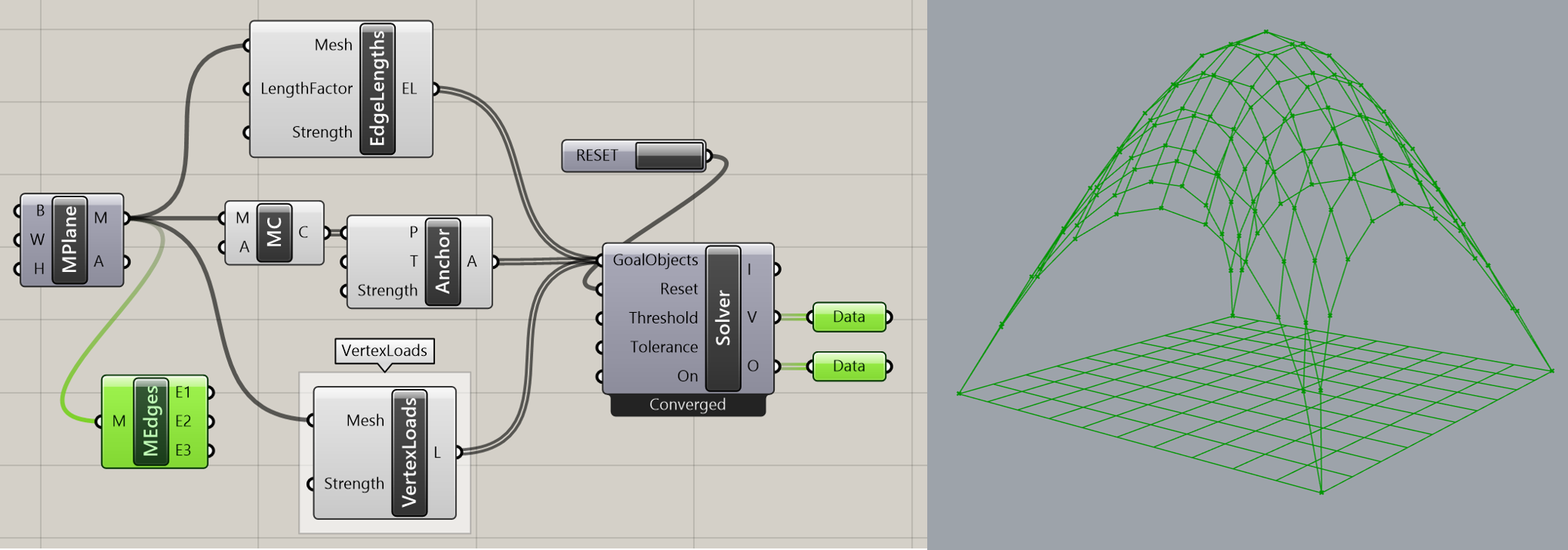
詳細１：正方形メッシュの4つ角を任意の点に固定して引っ張ったような形状をシミュレートした例。
ソルバーのToggleをTrueにすると計算が開始される。
主なコンポーネントの役割は以下の通り。
[EdgeLengths] → メッシュのエッジに強度を設定（バネのように振る舞う）
[MeshCorner（MC）] → メッシュの4つ角を抽出
[Anchor] → 入力した点（P）をターゲット点（T）に固定
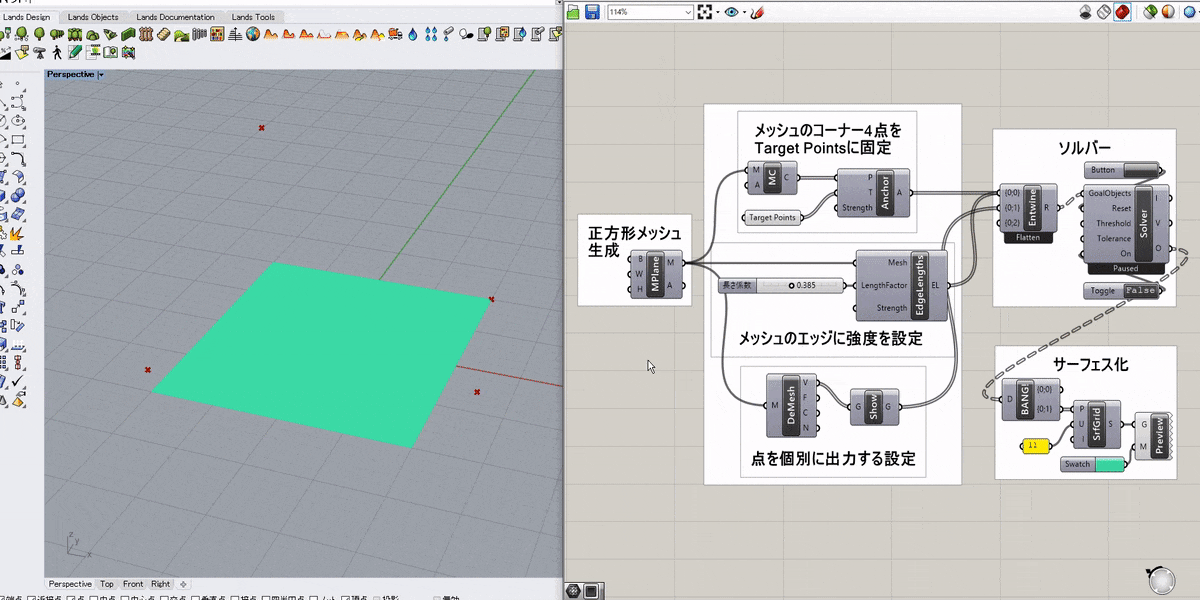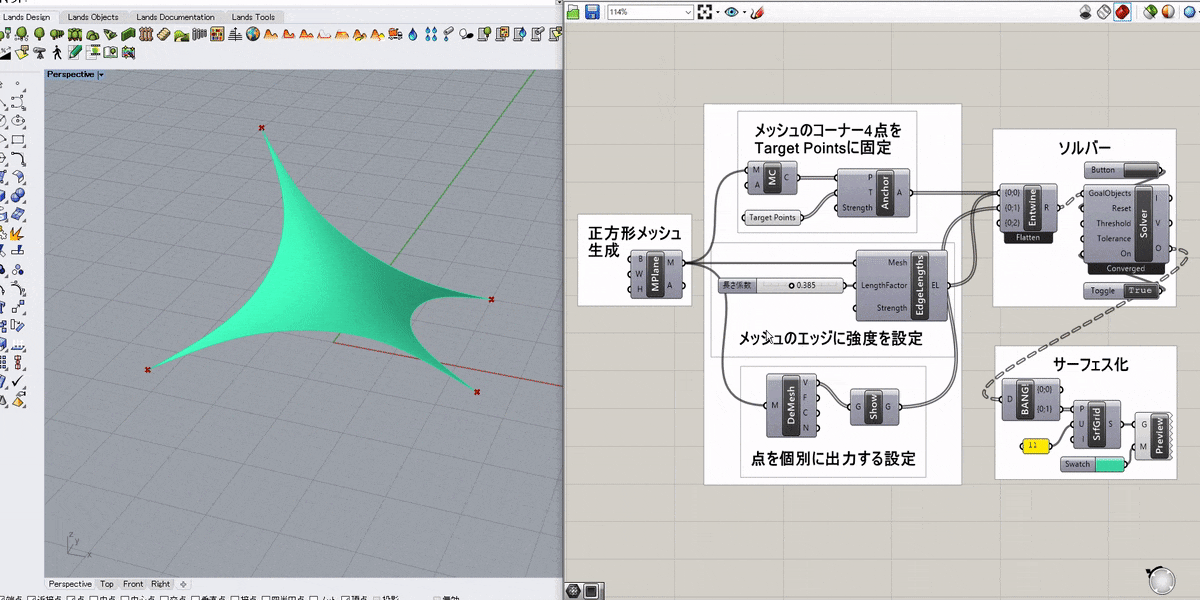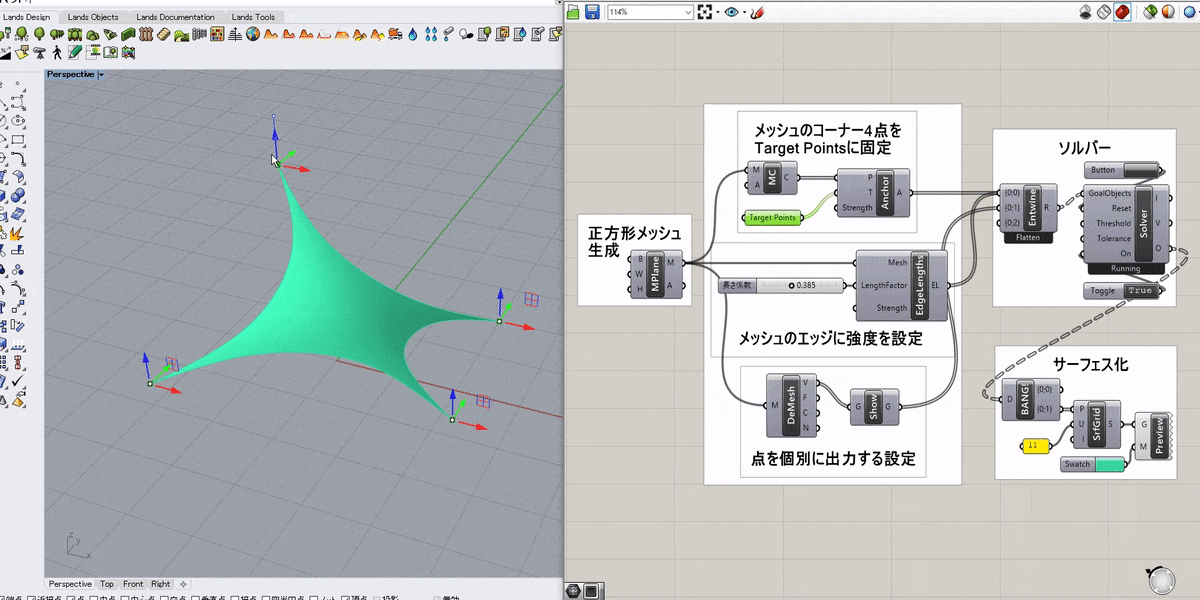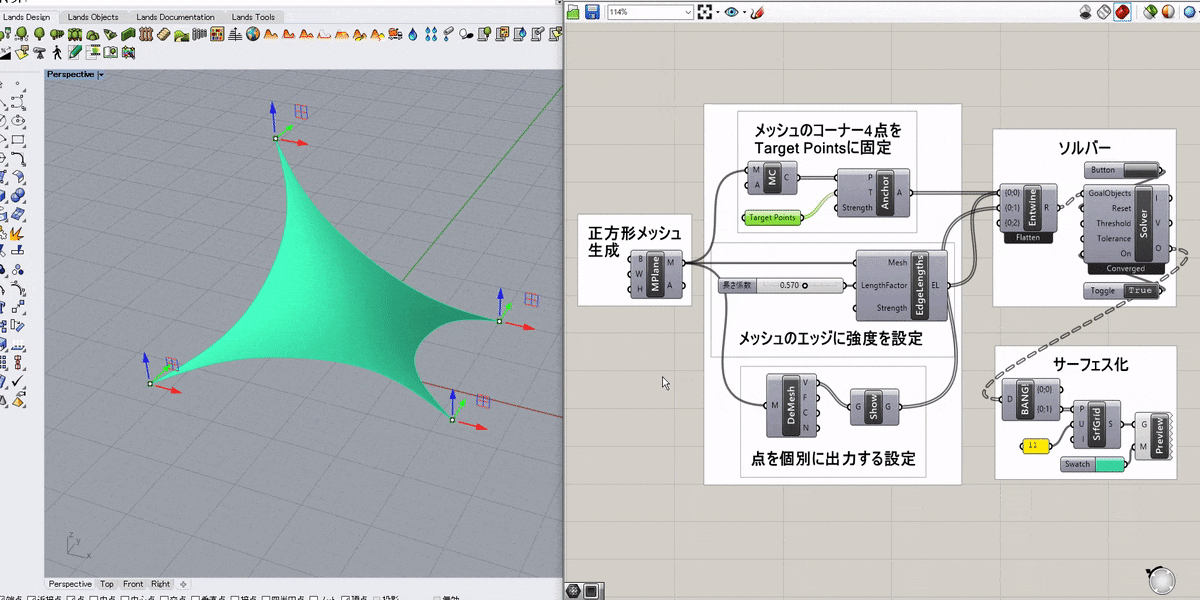
詳細２：メッシュのエッジに強度を設定するゴールオブジェクトには、[Length(Line)]というものもある。
両者の違いは、入力するオブジェクト。
[EdgeLengths] → メッシュを直接入力
[Length(Line)] → カーブ（直線）を入力
Hinge
B
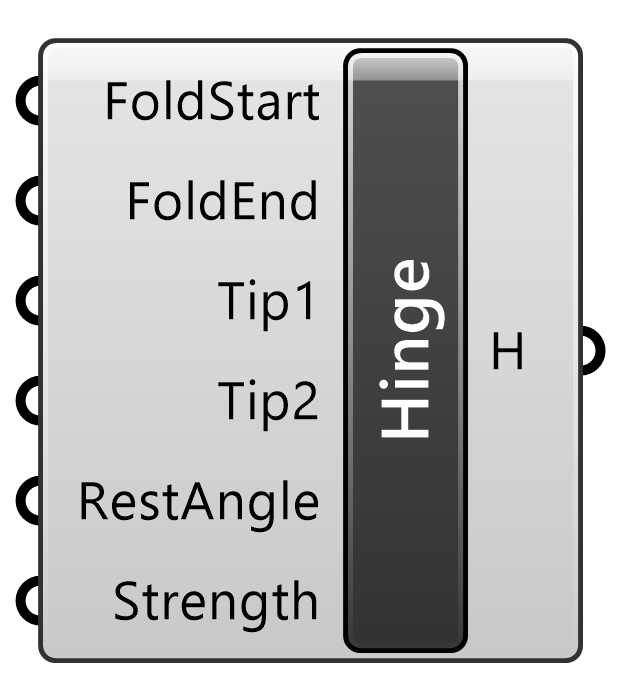
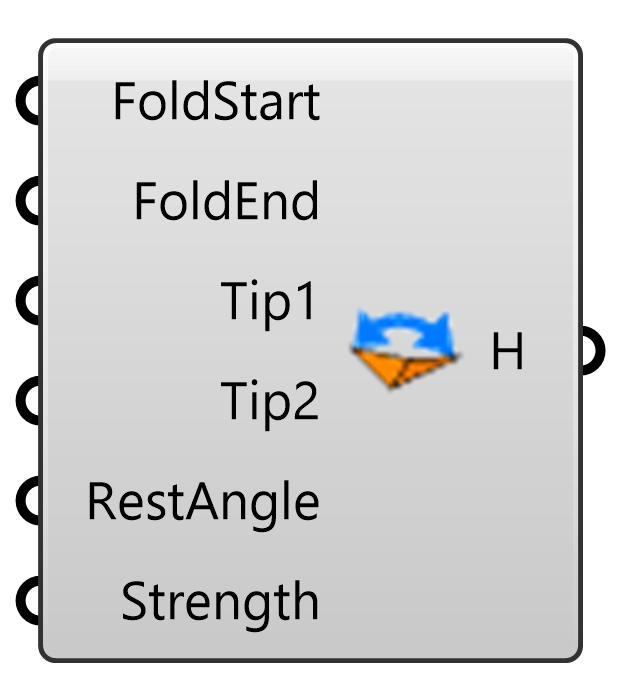
Kangaroo2＞Goals-Mesh
ヒンジの折り曲げの端点と先端を指示し、指定した角度（RestAngle）に折り曲げるゴールオブジェクト。角度はラジアンで入力する。Solverに接続して用いる。
Isothermic
C
Kangaroo2＞Goals-Mesh
S-Isothermicメッシュを生成するゴールオブジェクト。Solverに接続して用いる。
LiveSoap
C
Kangaroo2＞Goals-Mesh
極小曲面、または平均曲率一定曲面（CMC曲面）を生成するためのゴールオブジェクト。UseVolume（U）にTrueを入れるとCMC曲面、Falseを入れると極小曲面となる。Reset（R）で計算がリセットできる。Solverに接続して用いる。
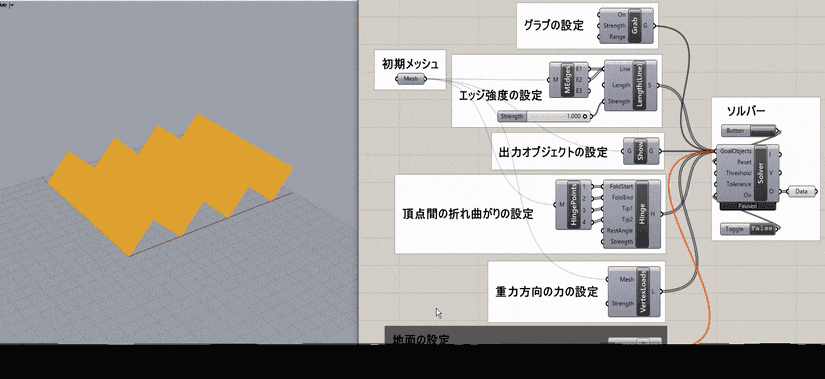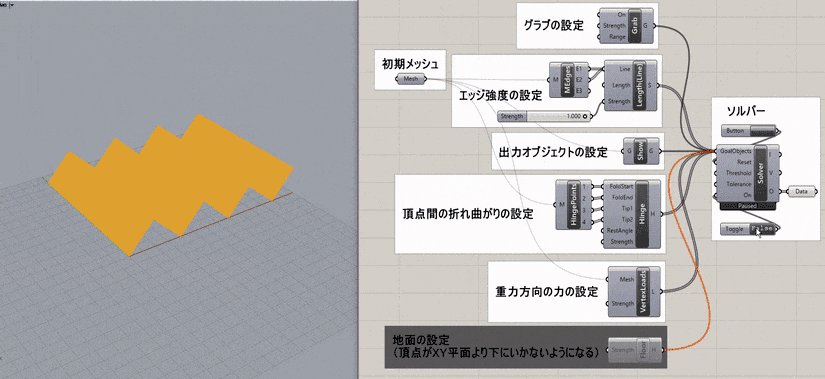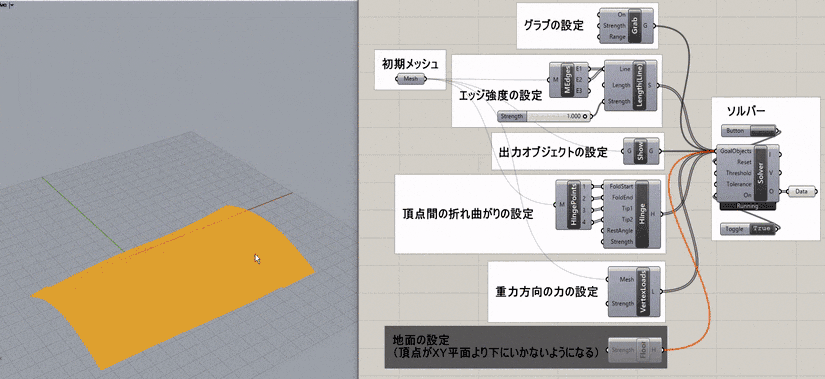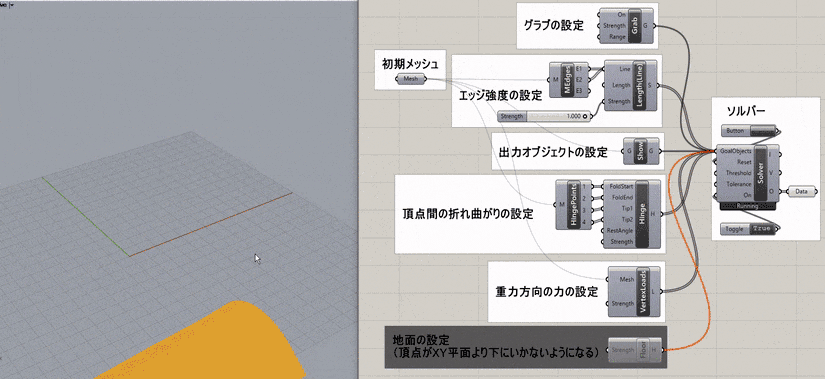
NoFoldThrough
C
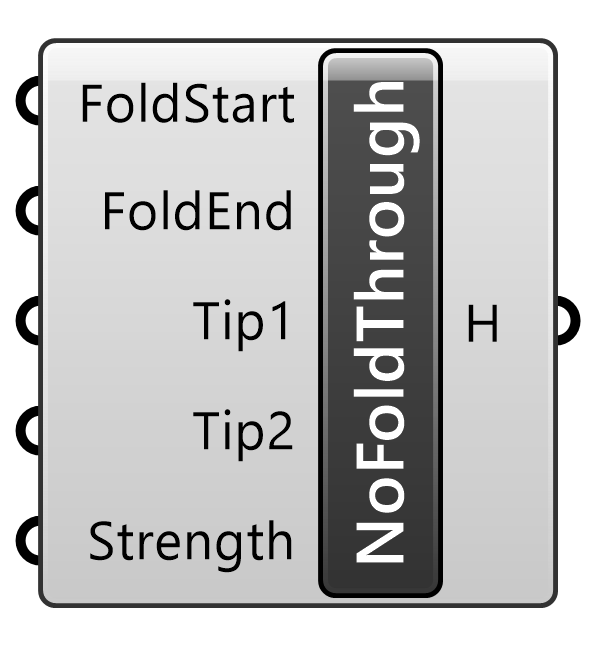
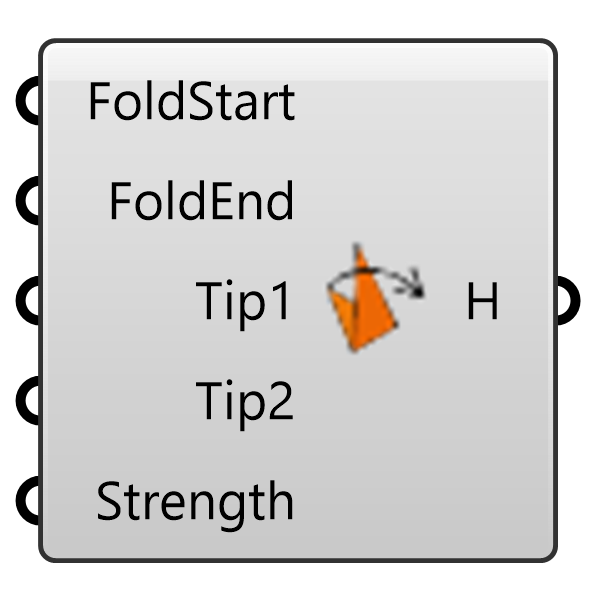
Kangaroo2＞Goals-Mesh
ヒンジの折り曲げの端点と先端を指示し、折り目のない状態に展開するゴールオブジェクト。Solverに接続して用いる。
Planarize
B
Kangaroo2＞Goals-Mesh
メッシュ内のそれぞれの4点の頂点を同一平面上に維持するゴールオブジェクト。Solverに接続して用いる。
PlasticHinge
C
Kangaroo2＞Goals-Mesh
ヒンジの折り曲げの端点と先端を指示し、指定した角度（RestAngle）に折り曲げるゴールオブジェクト。角度が上限値（Limit）に達するまでは、ヒンジ角度が弾性的に変形するよう保持する。角度はラジアンで入力する。Solverに接続して用いる。
PolygonArea
C
Kangaroo2＞Goals-Mesh
入力された閉じたポリライン（Polyline）で囲まれた領域の面積を設定するゴールオブジェクト。Solverに接続して用いる。
Pressure
B
Kangaroo2＞Goals-Mesh
入力されたメッシュ（Mesh）のそれぞれの三角形メッシュに、その面積に比例した法線方向の力を与えるゴールオブジェクト。Solverに接続して用いる。
Smooth
A
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）の頂点の配置が可能な限り滑らかになるように維持するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細１：作成したメッシュを任意のサーフェス上に貼り付けるアルゴリズムの例。
ソルバーのToggleをTrueにすると計算が開始される。
単純に[OnMesh]を使って貼り付けると、無理やり移動しているのでメッシュがガタついてしまう。
[Smooth]を付けることでメッシュのエッジがスムーズな状態を保ったまま貼り付けられるようになる。
SoapFilm
B
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）を、石鹸膜（Soapfilm）の形状を表現する平均曲率=0の極小曲面に変形するゴールオブジェクト。Solverに接続し、TangentialSmoothコンポーネントと組み合わせて用いる。
TangentialSmooth
B
Kangaroo2＞Goals-Mesh
Soapfilmコンポーネントで生成された曲面がスムーズになるようにするゴールオブジェクト。Solverに接続し、Soapfilmコンポーネントと組み合わせて用いる。
TangentIncircles
B
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）のそれぞれの三角形メッシュの内接円が接するように変形するゴールオブジェクト。Solverに接続して用いる。
VertexLoads
A
Kangaroo2＞Goals-Mesh
入力されたメッシュ（Mesh）の頂点を抽出し、その頂点に垂直荷重を与えるゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
任意の点ではなく、メッシュのすべての頂点に対し荷重を掛けたい場合は、[VertexLoads]ゴールオブジェクトが点ではなくメッシュを直接入力できるので便利である。
詳細1：図の例は入力したメッシュのコーナー4点を拘束し、頂点すべてに[VertexLoads]で＋Z軸方向の荷重を与えたカテナリーメッシュである。
メッシュの頂点に限らず、剛体上や曲線上の任意の点を指定し荷重を定義したい場合は[Load]ゴールオブジェクトを用いる。
Volume
B
Kangaroo2＞Goals-Mesh
入力したメッシュ（Mesh）の体積（V）を設定するゴールオブジェクト。Vに何も入力しない場合は元の体積が維持される。Solverに接続して用いる。
Wind
B
Kangaroo2＞Goals-Mesh
入力されたメッシュ（M）に対して、風を定義するゴールオブジェクト。風の向きと強さはベクトル（W）で指定する。Solverに接続して用いる。
Goals-On
OnCurve
A
Kangaroo2＞Goals-On
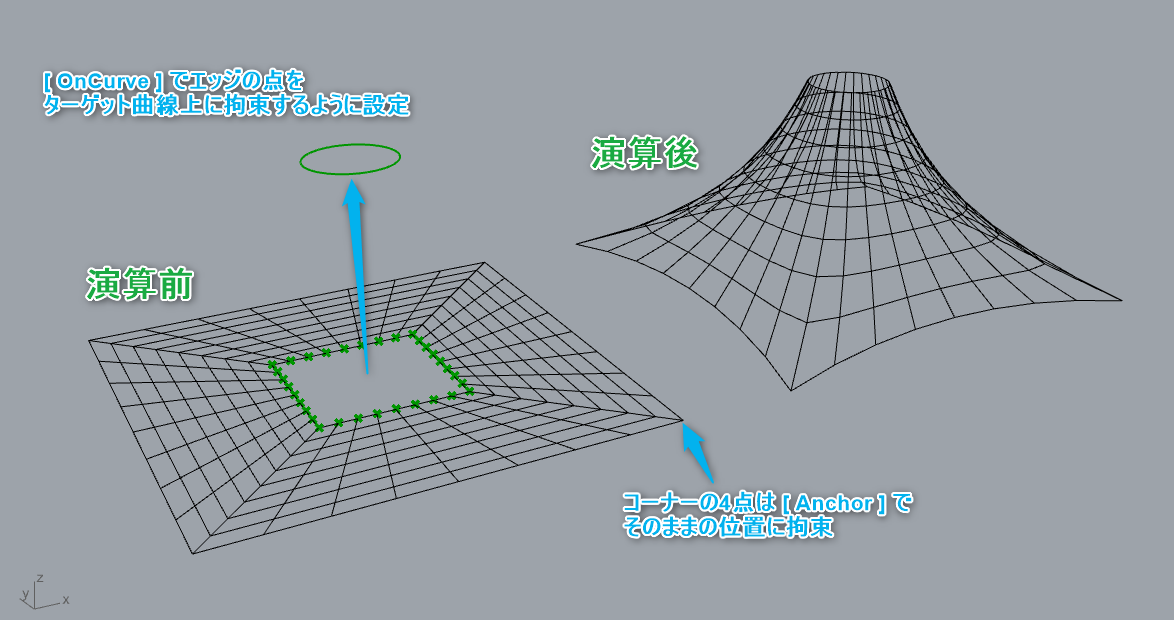
入力された点（Points）を曲線（Curve）上に拘束するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
点をある位置に拘束するための主なゴールオブジェクトは、Anchor系とOn系に分けられる。On系には[OnCurve／OnMesh／OnPlane]があり、これらを用いると点は入力されたジオメトリや指定した平面上に拘束されるが、その上では自由に動くことができるという設定となる（それに対し、Anchor系は点を点に拘束するためのゴールオブジェクト）。
詳細1：図は、作成したメッシュの一部のエッジをサークル状の曲線に拘束した例である。物理演算の結果として得られた形状であるため、実際に網を上方向に引っ張ってサークル状のレールに取り付けたような形状となっている。コーナーの4点は[Anhcor]で拘束しているので上方向に引っ張られても元の位置から動いていない。
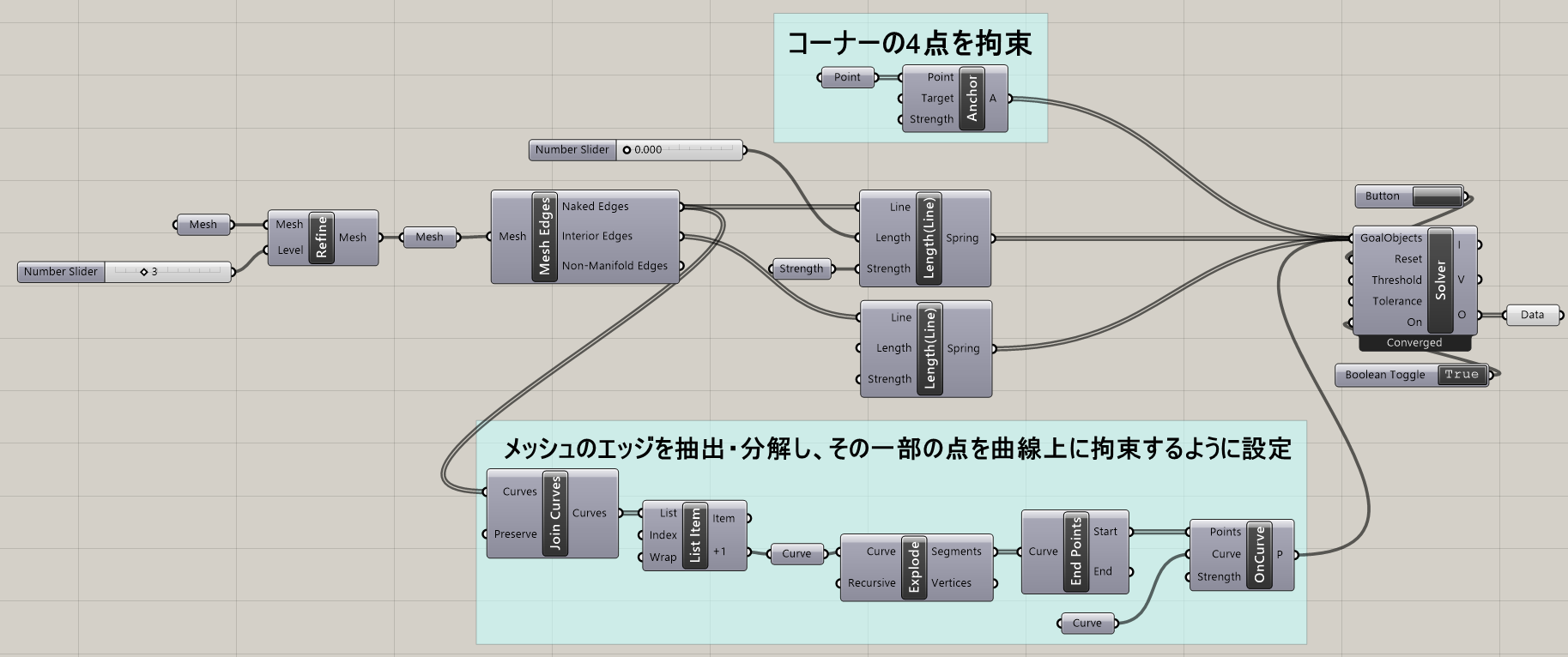
OnMesh
A
Kangaroo2＞Goals-On
入力された点（Points）をメッシュ表面（Mesh）上に拘束するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
点をある位置に拘束するための主なゴールオブジェクトは、Anchor系とOn系に分けられる。On系には[OnCurve／OnMesh／OnPlane]があり、これらを用いると点は入力されたジオメトリや指定した平面上に拘束されるが、その上では自由に動くことができるという設定となる（それに対し、Anchor系は点を点に拘束するためのゴールオブジェクト）。
詳細1：図は、あるメッシュサーフェス上に円を敷き詰める過程（サークルパッキング）を定義したアルゴリズムの例とその結果である。[OnMesh]ゴールオブジェクトにより、入力された点はメッシュサーフェス上に拘束されている。
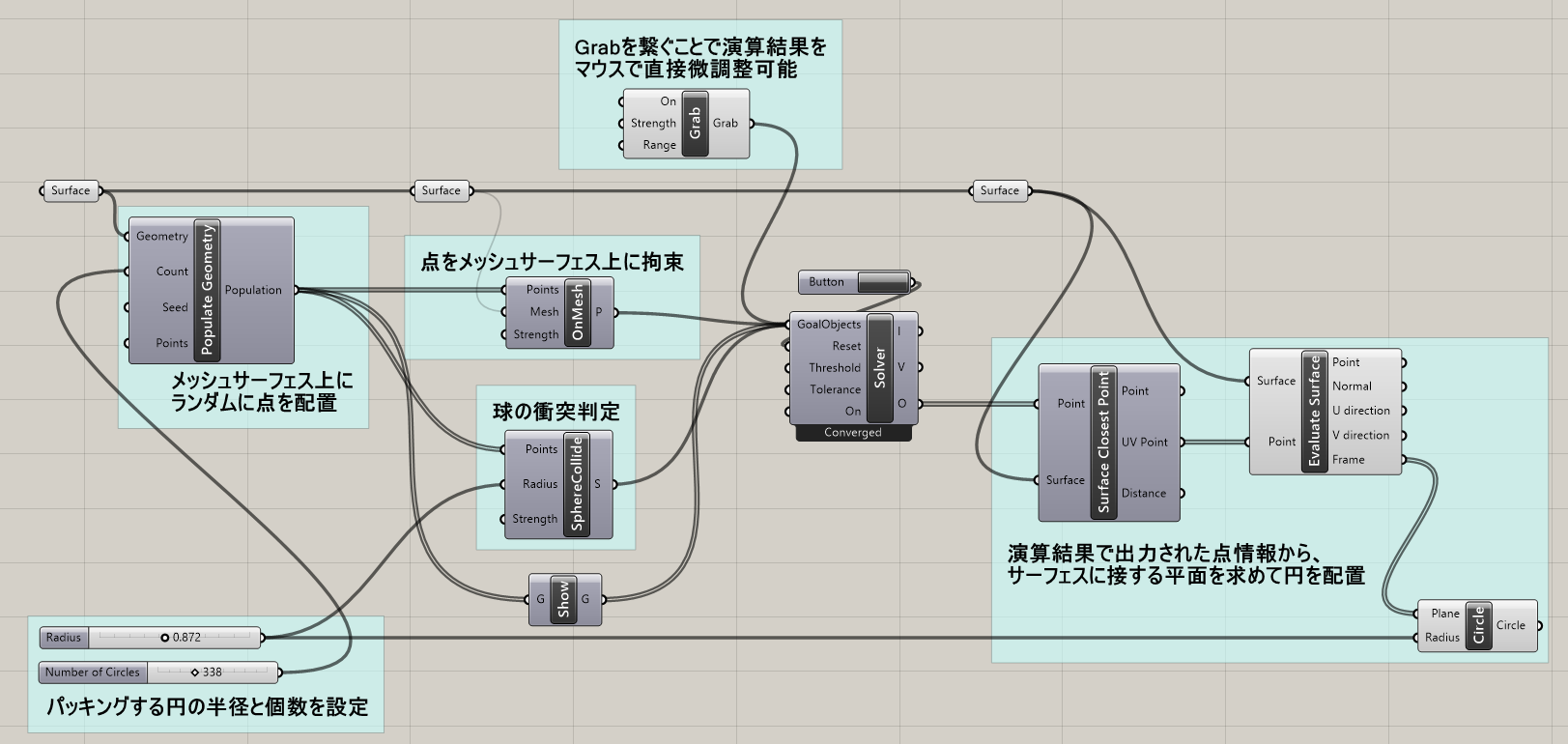
詳細2：ソルバーがONの状態であれば、スライダーで半径や個数を変更したり、[Grab]で点を動かした場合の条件がリアルタイムに反映される。円を敷き詰めた後に半径を小さくし直せば、図のようにそのままの位置で小さい円を均等に配置するようなデザインも可能だ。
OnPlane
A
Kangaroo2＞Goals-On
入力された点（Points）を平面（Plane）上に拘束するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
点をある位置に拘束するための主なゴールオブジェクトは、Anchor系とOn系に分けられる。On系には[OnCurve／OnMesh／OnPlane]があり、これらを用いると点は入力されたジオメトリや指定した平面上に拘束されるが、その上では自由に動くことができるという設定となる（それに対し、Anchor系は点を点に拘束するためのゴールオブジェクト）。
詳細1：図は、ある矩形領域内に[populate2D]コンポーネントによって無作為に配置された点に対し、[Load]ゴールオブジェクトによってY軸方向の荷重を掛けた例である。オブジェクトは3次元空間内に配置されているが、[OnPlane]ゴールオブジェクトにより、XY平面に拘束されているので、平面や曲線、点などの2Dのオブジェクト同士でも物理演算が可能だ。
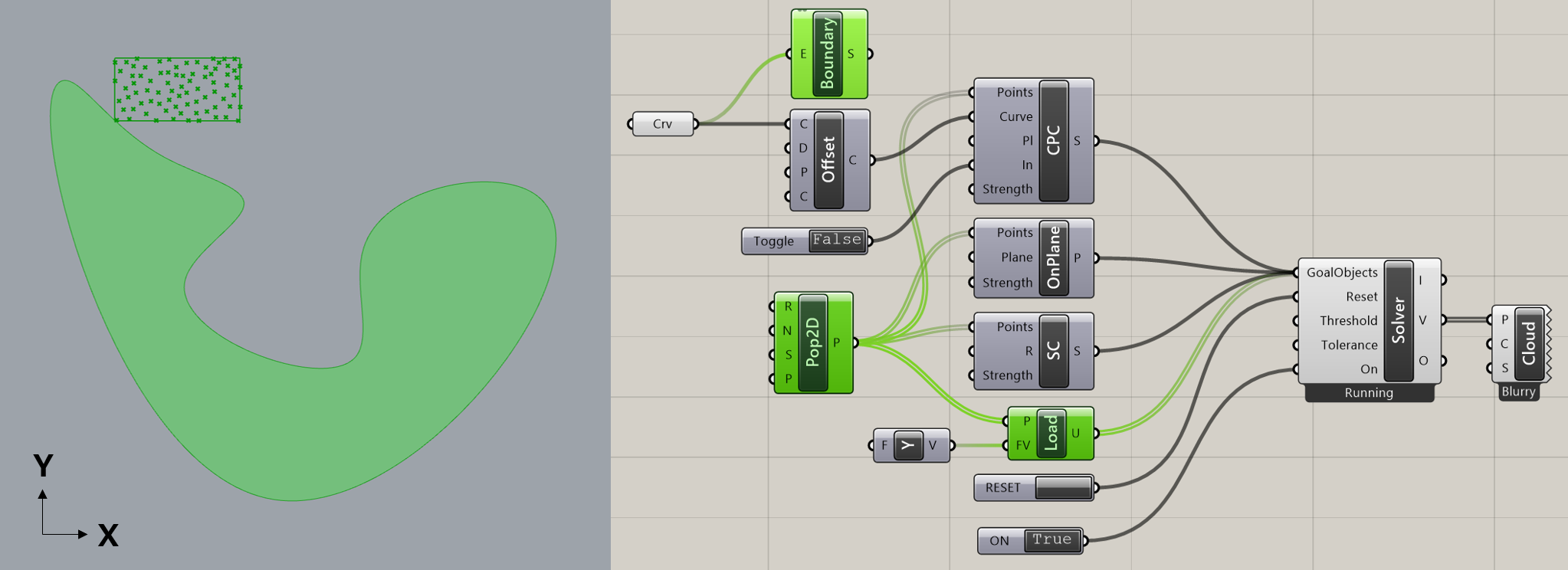
Goals-Pt
Anchor
A
Kangaroo2＞Goals-Pt
入力された点（P）を拘束するゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
点をある位置に拘束するための主なゴールオブジェクトは、Anchor系とOn系に分けられる。On系には[OnCurve／OnMesh／OnPlane]があり、入力されたジオメトリ上に点を拘束するため、そのジオメトリや指定した平面上では自由に動くことができる。
Anchor系は[Anchor]と[AnchorXYZ]の2種類がある。[Anchor]は、On系の名称に倣えば「OnPoint」のようなもので、並進3自由度を拘束する。[AnchorXYZ]は拘束する自由度をX/Y/Zの3種類からTrue/Falseで選択できる。いずれも回転自由度は拘束されない。
詳細1：図の例は上方向に荷重を掛けたカテナリーの1種であるが、メッシュの4辺の内、２つの辺の点は[AnchorXYZ]によってZ軸方向の自由度が拘束されているため、XY平面でスライドするような動きになっている。コーナーの4点は[Anchor]に繋がれているため動かない。
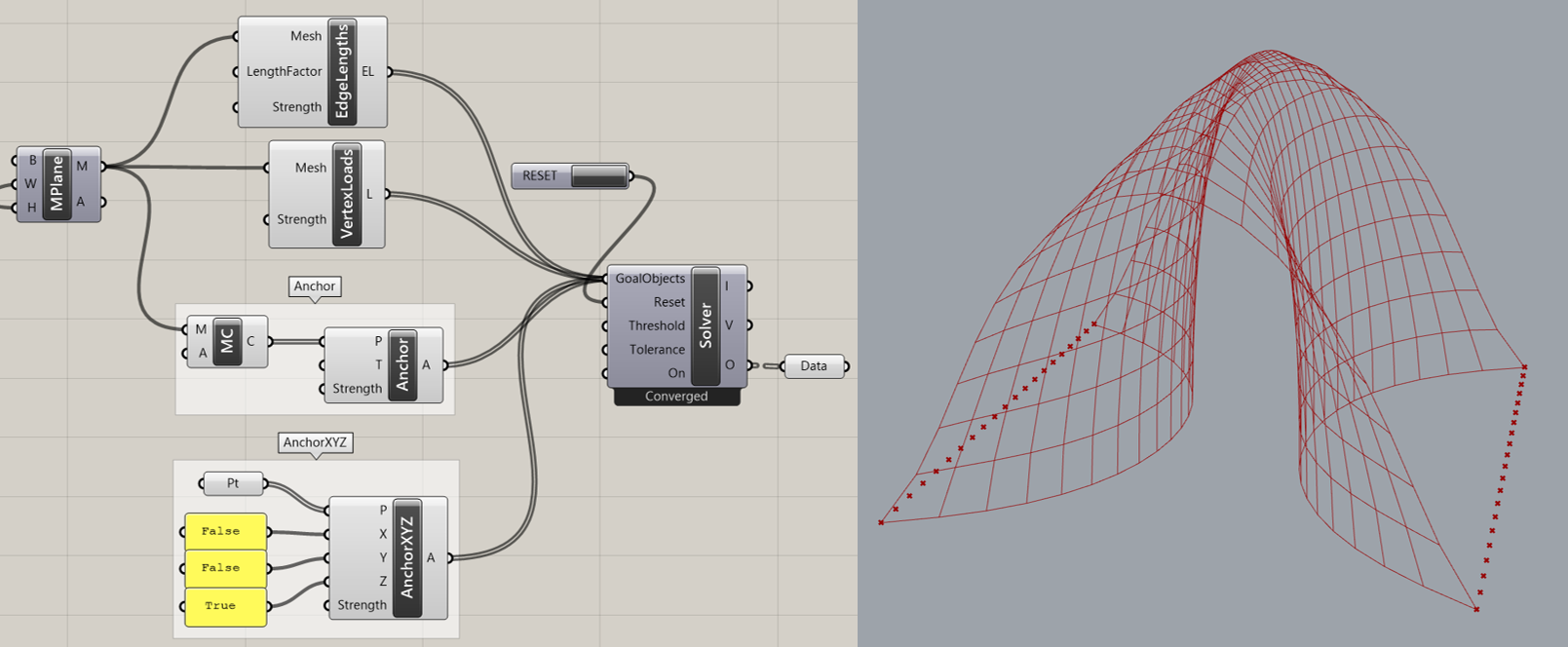
AnchorXYZ
A
Kangaroo2＞Goals-Pt
入力された点（P）を特定の方向にのみ拘束するゴールオブジェクト。拘束する方向は入力に「True」を、拘束しない方向は入力に「False」を入力する。Solverに接続して用いる。
サンプルデータをダウンロードできます
点をある位置に拘束するための主なゴールオブジェクトは、Anchor系とOn系に分けられる。On系には[OnCurve／OnMesh／OnPlane]があり、入力されたジオメトリ上に点を拘束するため、そのジオメトリや指定した平面上では自由に動くことができる。
Anchor系は[Anchor]と[AnchorXYZ]の2種類がある。[Anchor]は、On系の名称に倣えば「OnPoint」のようなもので、並進3自由度を拘束する。[AnchorXYZ]は拘束する自由度をX/Y/Zの3種類からTrue/Falseで選択できる。いずれも回転自由度は拘束されない。
詳細1：図の例は上方向に荷重を掛けたカテナリーの1種であるが、メッシュの4辺の内、２つの辺の点は[AnchorXYZ]によってZ軸方向の自由度が拘束されているため、XY平面でスライドするような動きになっている。コーナーの4点は[Anchor]に繋がれているため動かない。
Bomb
B
Kangaroo2＞Goals-Pt
設定した時間（Detonation）に設定した位置（Lacation）付近にある点（Points）を吹き飛ばすゴールオブジェクト。時間はIteration回数で指定する。Solverに接続して用いる。
Coincident
B
Kangaroo2＞Goals-Pt
入力された点（P0／P1）同士の距離がゼロとなるように変形するゴールオブジェクト。Solverに接続して用いる。
Floor
A
Kangaroo2＞Goals-Pt
床を設定するゴールオブジェクト。worldXY平面が床となる。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細１：メッシュに重力方向の力を掛け、布のような振る舞いをシミュレートした例。
ソルバーのToggleをTrueにすると計算が開始される。
重力方向に力が掛かっているが、[Floor]を設定することで、XY平面上に留まり、地面に布をひろげたような振る舞いとなる。
詳細2：[Floor]が無いと落下していってしまう。
FloorFriction
C
Kangaroo2＞Goals-Pt
摩擦を持つ床を設定するゴールオブジェクト。worldXY平面が床となる。Points（P）に摩擦を考慮する点、Limit(L)に摩擦の強さ（0の場合摩擦ゼロ）を入力する。Solverに接続して用いる。
Load
A
Kangaroo2＞Goals-Pt
入力された点（P）に、ベクトル（ForceVector）で指定した荷重を与えるゴールオブジェクト。Solverに接続して用いる。
サンプルデータをダウンロードできます
詳細1：上図は、ある矩形領域内に[populate2D]コンポーネントによって無作為に配置された点に対し、[Load]ゴールオブジェクトによってY軸方向の荷重を掛けた例である。衝突用のジオメトリやFloorを定義すれば、下図のようなシミュレーションが可能だ。
任意の点ではなく、メッシュのすべての頂点に対し荷重を掛けたい場合は、[VertexLoads]ゴールオブジェクトの方が点ではなくメッシュを直接入力できるので便利である。
MagnetSnap
C
Kangaroo2＞Goals-Pt
入力された点（Points）同士が設定された距離（R）内にあれば自動的に磁石のように吸着されるようにするゴールオブジェクト。Solverに接続して用いる。
PlasticAnchor
B
Kangaroo2＞Goals-Pt
拘束が解除される距離（L）を設定し、制限付きで入力された点（P）に拘束条件を与えるゴールオブジェクト。Solverに接続して用いる。
Transform
C
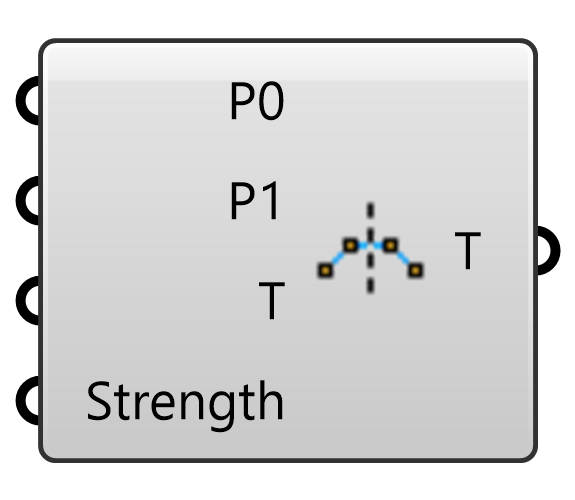
Kangaroo2＞Goals-Pt
2点間に与えられた変形を維持するゴールオブジェクト。Solverに接続して用いる。
Main
BouncySolver
B
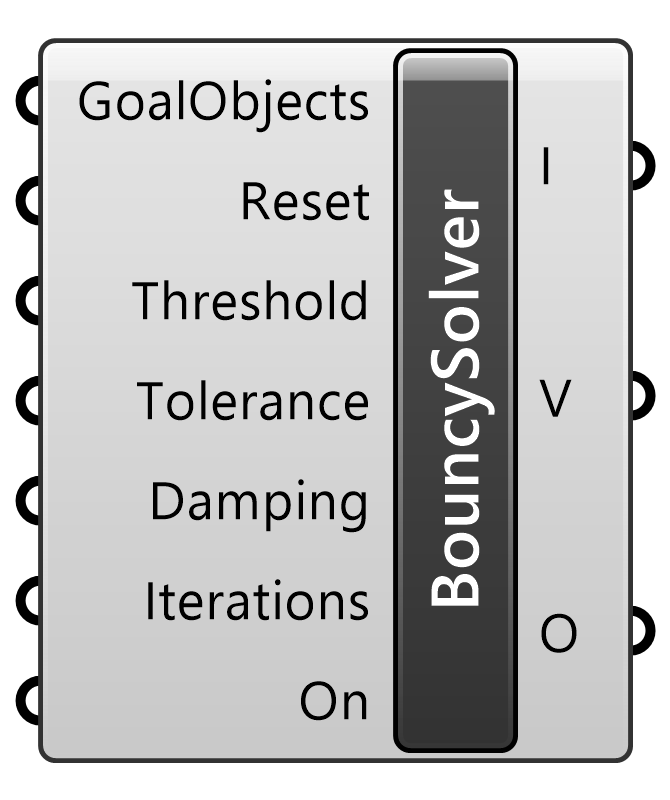
Kangaroo2＞Main
ゆっくり収束するソルバー。実際には運動中にも関わらず、一時的に運動が止まり通常のソルバーでは収束したと見なされてしまう場合などに用いる。減衰（Damping）の設定が必要。ゴールオブジェクト（GoalObjects）を入力するとソルバーが実行され、その結果として点（V）やオブジェクト（O）が出力される。Resetを「True」にすると演算結果がリセットされる。
Grab
A
Kangaroo2＞Main
このコンポーネントをSolverのGoalObjectsに接続しておき、On入力を「True」にしておくと、Rhinoのビュー上でAltキーを押しながらプレビュー結果をマウスで変形することができる。
サンプルデータをダウンロードできます
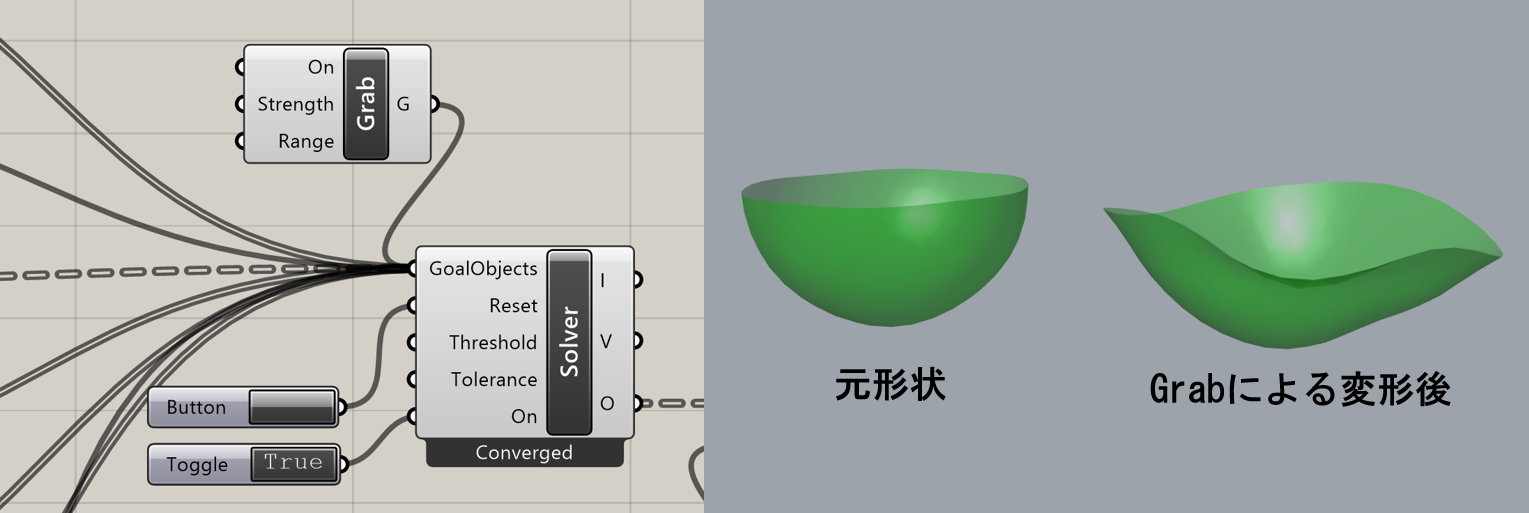
このとき、SolverはONとなっている必要がある。Grabは入力条件をマウスで与えているようなものなのでOFFだと演算ができずGrabは機能しない（つまり、最終的な結果しか表示できないZombieSolverでは[Grab]は使用できない）。左マウスボタンを離すとGrabによる入力をもとに演算が継続される。Grabしたままの形状を維持してBakeしたい場合などは、Grabで変形後に「Ctrl」キーを長押しするとその形状が維持される。
詳細1：下図は[Grab]によってお椀型の器の形状を変形させた例である。
Show
A
Kangaroo2＞Main
このコンポーネントに入力されたジオメトリは、Solver実行後にSolverのO出力（GoalFunction Outputs）から別のツリーとして出力される。ツリーを分解すればプレビューやBake用に任意のジオメトリを抽出することができる。Solverに接続して用いる。
サンプルデータをダウンロードできます
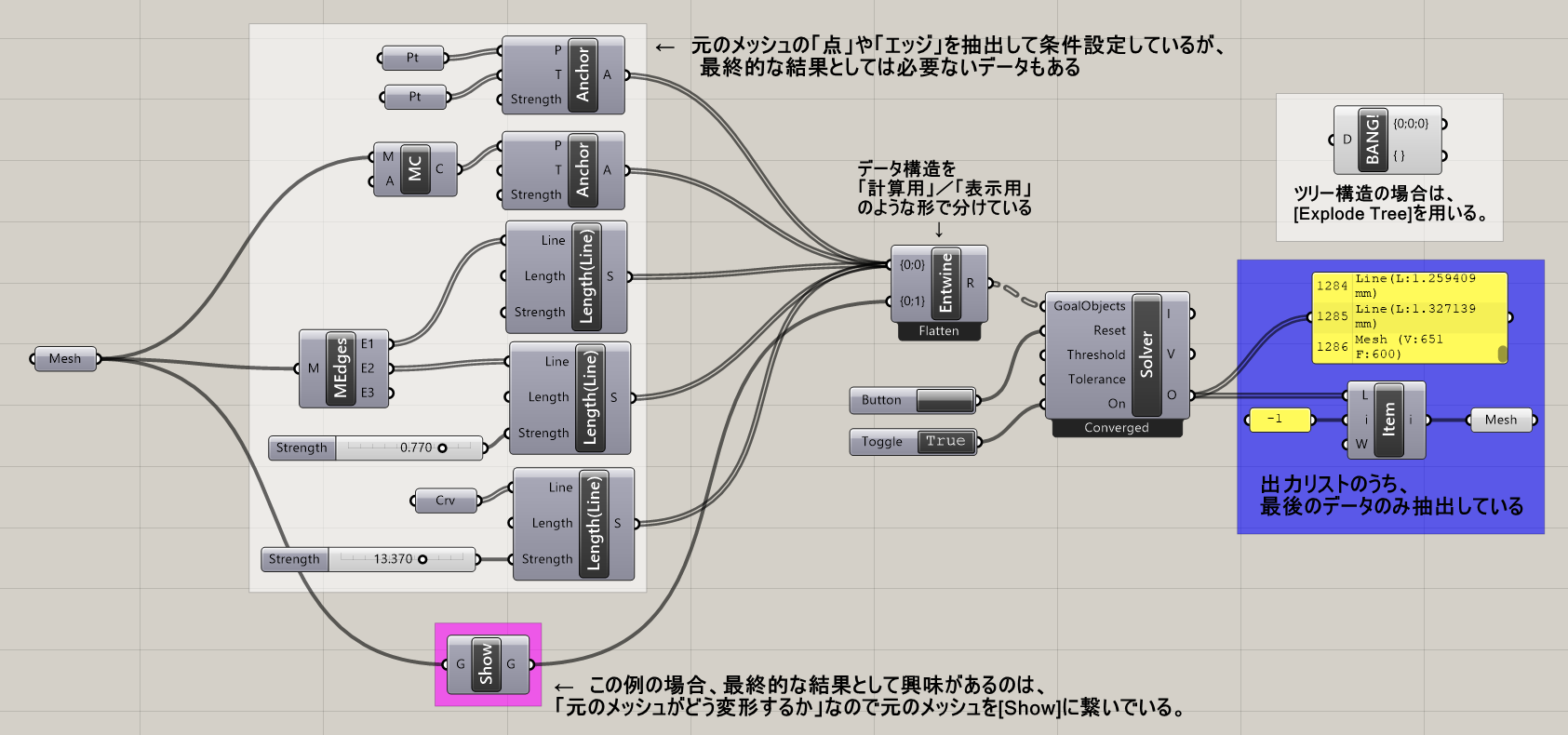
Kangaroo2では、各入力オブジェクトの点やエッジなどを適宜、抽出・加工し、条件を与えた上で物理演算を行うが、最終的に出力したいデータはそれらの一部であることが多い。条件はすべてSolverのGoalObjects入力に接続してしまうのでその中から必要なものだけ抽出するのはそのままでは困難である。
[Show]ゴールオブジェクトを用いれば、最終的に出力したい元オブジェクトを他のゴールオブジェクトとデータ構造を分けておくことができる。さらにEntwineなどのツリーを結合するコンポーネントなども合わせて用いれば、データ構造が明確になりゴールオブジェクトが複雑になった場合でもわかりやすくなるだろう。抽出したいデータが出力リストの一番前か一番後ろになるようにしておけば、[List item]コンポーネントや[Explode Tree]コンポーネントで簡単に抽出できる。
詳細1：下図の例では、拘束点やエッジ長さを定義するために、[MeshCorners]や[Mesh Edges]コンポーネントが用いられているが、最終的には元のメッシュがどのように変形するかを画面で確認したいので元のMeshだけにShowが繋がれている。さらにそれを[Entwine]に繋いでデータ構造を計算用と表示用で分けている。
Soft & Hard Solver
C
Kangaroo2＞Main
ソフトなゴール（SoftGoals）と拘束するハードなゴール（HardGoals）を別々に入力するソルバー。HardGoalsはSoftGoalsの結果を無視する。
Solver
A
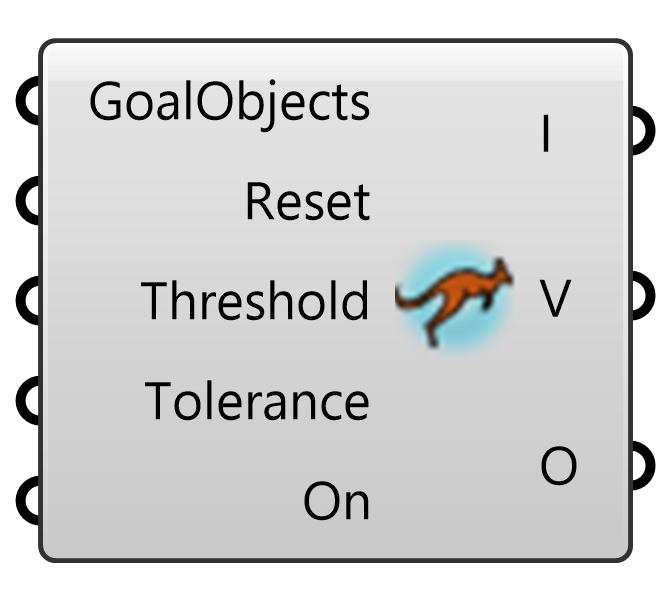
Kangaroo2＞Main
Kangaroo2の標準ソルバー。ゴールオブジェクト（GoalObjects）を入力するとソルバーが実行され、その結果として点（V）やオブジェクト（O）が出力される。Resetを「True」にすると演算結果がリセットされる。Onを「False」にしない限り、演算が繰り返される。特に問題がない場合はこのソルバーを用いれば良い。
サンプルデータをダウンロードできます
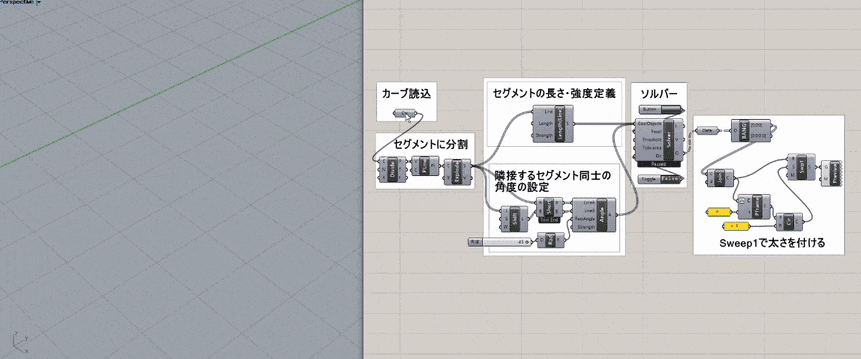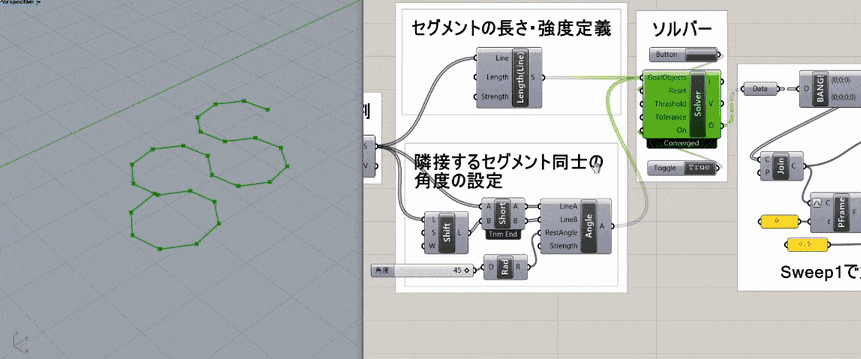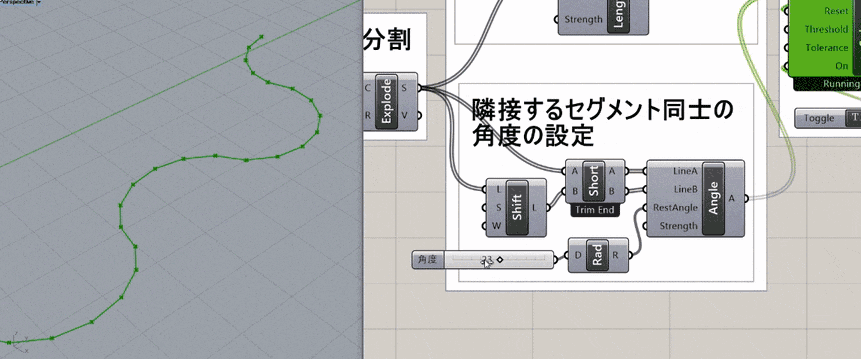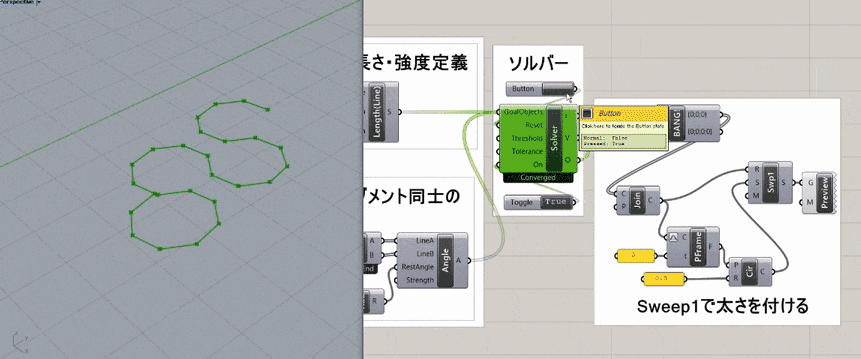
[Solver]コンポーネントの機能の解説のために、Kangaroo2による物理演算のフローを示す。
典型的なKangaroo2の定義ファイル作成におけるコンポーネントの役割は図1のように大きく分けて6つに分類できる。
１．元ジオメトリ準備： まず物理演算の対象となるジオメトリを用意する。これはRhinoから読み込む方法とGH上で定義する方法がある。
２．ゴールオブジェクト用データ準備： 拘束条件や荷重条件などを設定するために、頂点やエッジの抽出、加工、数値の設定などを行う。
３．ゴールオブジェクト： Kangaroo2で予め用意されているゴールオブジェクト群を用いてソルバー計算の条件を定義する。
４．データ構造整理： 必須ではないが、ソルバー計算後の出力結果を効率良く抽出するためにソルバー入力前にデータ構造を整理しておくと良い。計算用／表示用などで分けることが多い。
５．ソルバー： GoalObjectsに入力された条件を満たす解を物理演算により求める。Resetを”True”にすると演算結果がリセットされる（[Botton]コンポーネントを繋いでおくと使いやすい）。物理演算前後の解の差がThreshold（閾値）で設定した値以下になると計算が”Converged（収束）”する。点同士が同一の点かどうかを判断する許容差はToleranceで設定する。On入力が”True”で物理演算が実行され、”False”にすると中断される。I出力からはIteration（演算のステップ数）、V出力からは頂点、O出力からはオブジェクト情報が出力される。
６．出力データの加工： GoalObjectsに繋いだ入力の内、任意のデータのみ抽出する場合は、４で定義したデータ構造に合わせて[List item]や[Explode Tree]コンポーネントを用いて取り出す。出力結果はメッシュデータなのでサーフェス化したい場合は、頂点を出力し再度サーフェス化する必要がある。
Kangaroo2のソルバーはいくつか種類があるが、通常はこの[Solver]コンポーネントを用いれば良い。その他、演算過程を観察したりアニメーションにしたい場合は[ZombieSolver]を、動きのある問題で[Solver]がうまく機能しない場合は[BouncySolver]を試してもらいたい。
StepSolver
C
Kangaroo2＞Main
アニメーション作成用にSubIterationsを設定可能なソルバー。ZombieSolverでもほぼ同様の結果が得られるが、BouncySolverを使うような演算ではZombieSolverだとエラーが生じるためこちらを用いる。
ZombieSolver
A
Kangaroo2＞Main
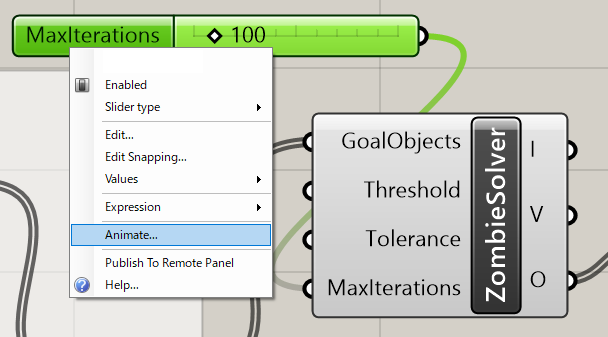
繰り返し回数指定用のソルバー。ゴールオブジェクト（GoalObjects）を入力するとソルバーが実行され、その結果として点（V）やオブジェクト（O）が出力される。通常のKangaroo2のSolverコンポーネントとの違いは、繰り返し回数（MaxIterations）を指定し最後の結果のみ出力する点である。MaxIterationsにスライダーを接続することで時間変化のアニメーションを作成することができる。
サンプルデータをダウンロードできます
詳細1：Animate機能は、左図のように[Number Slider]の右クリックメニューから実行できる。アニメーションの例が右図である。
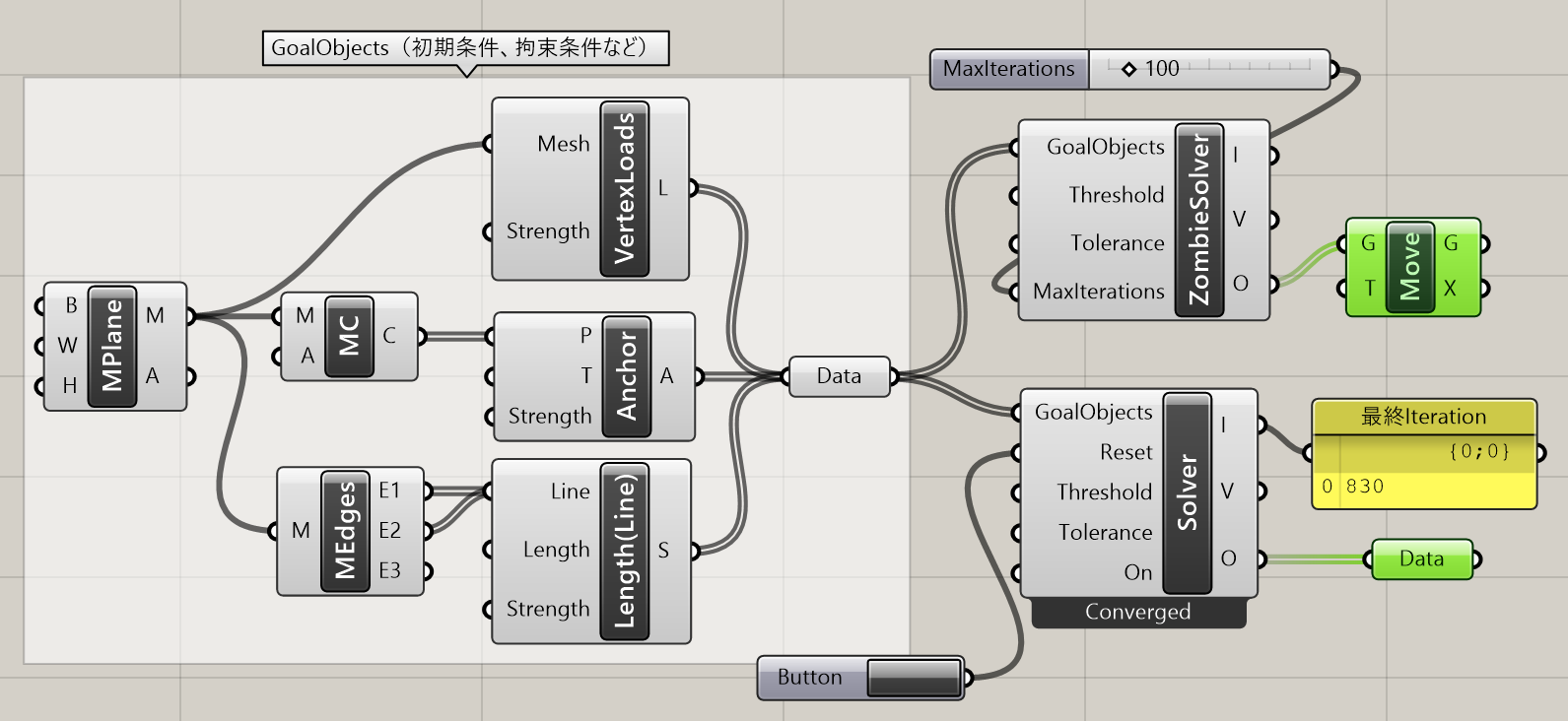
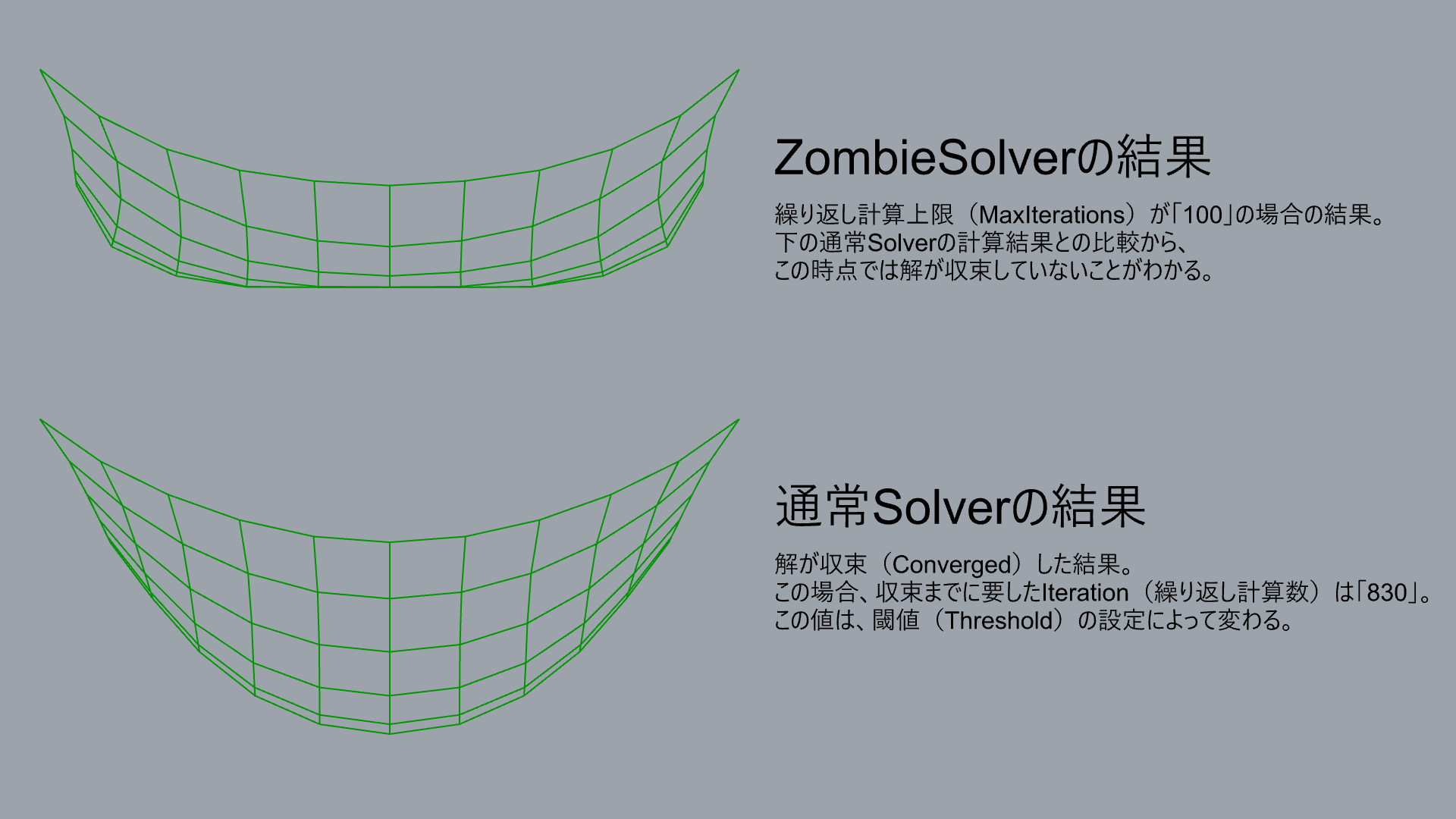
詳細2：Kangaroo2は物理演算プラグインなので、与えられたGoalObjects（初期条件や拘束条件）を満たす解を繰り返し計算により求める。通常の[Solver]や[BouncySolver]は、それぞれの繰り返し計算の各ステップ前後の解の差が閾値（Threshold）内に収まったら”解が収束した（もうそれ以上動かない）”と判断し、ソルバー計算が終了する。途中の結果も見ることはできるが止めたい場合は手動でOn入力を”False”にしないといけない。これらに対し、[ZombieSolver]は収束する・しないに関わらず、”繰り返し計算を何回行うか（MaxIterations）”を指定してその時点での結果を出力するソルバーである。物理演算は条件の与え方次第では解が収束しないことがあるが、[ZombieSolver]を用いれば何かしらの結果は出力できることになる。
ただし、収束しないということは計算がただ不安定な場合もあるのでその結果が正しいとは限らず、またMaxIterationsが不十分だと計算途中の結果が出力され、それが最終結果だと勘違いしてしまうこともあるので注意が必要だ。用途に応じて使い分けたい（下図参照）。
Mesh
Bipartite
C
Kangaroo2＞Mesh
オーセティック構造を作るためにメッシュ頂点を0と1に割り振ったリストを出力する。Checkerboardコンポーネントの頂点版のようなもの。https://discourse.mcneel.com/t/kangaroo-bipartite/125118
ByParent
C
Kangaroo2＞Mesh
入力したメッシュ（M）のそれぞれのメッシュ単位をRefine（さらに分割）する。
Checkerboard
C
Kangaroo2＞Mesh
入力されたメッシュ（M）のそれぞれの三角形、四角形メッシュに対してチェッカーボード柄（市松模様）のように、0と1を交互に割り振ったリスト（A）を出力する。出力されたリストとDispatchコンポーネントなどを組み合わせて用いる。
Combine&Clean
B
Kangaroo2＞Mesh
入力したメッシュ（Mesh）における重複した頂点あるいは余分な頂点を取り除く。
Diagonalize
B
Kangaroo2＞Mesh
入力した元のメッシュ（M）のそれぞれの四角形メッシュの対角線を新しいエッジとしてメッシュを再構築する。
FaceFaceOffset
C
Kangaroo2＞Mesh
対応するメッシュサーフェス間の距離（D）が一定になるように円錐メッシュをオフセットする。
FoldAngle
C
Kangaroo2＞Mesh
エッジを共有する2つの三角形メッシュ間の角度を計測し出力する。
HingePoints
B
Kangaroo2＞Mesh
入力されたメッシュ（M）のヒンジを生成するために必要となる4点を抽出する。
MeshCorners
A
Kangaroo2＞Mesh
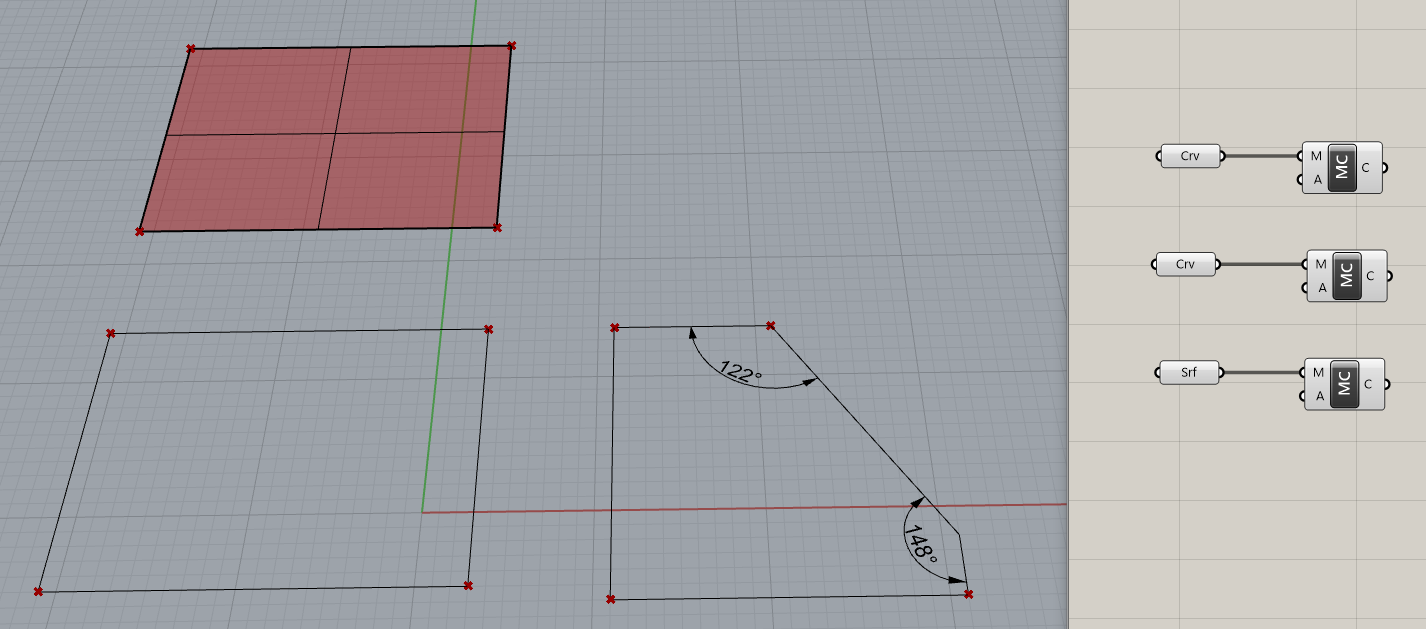
入力されたメッシュ（M）のコーナーに該当する点を抽出する。コーナーかどうかを判定する定義角（A）はラジアンで入力する。
サンプルデータをダウンロードできます
詳細1：図の例では、90°の頂点以外にも122°の頂点もコーナー点として抽出されている。それに対し、148°の頂点はコーナー点として抽出されていない。
[MeshCorners]は、Kangaroo2のコンポーネントではあるが、Solverに繋ぐ必要はないためKangarooの物理演算を用いる場面以外にも活用できる非常に汎用性の高いコンポーネントだ。
MeshDirection
C
Kangaroo2＞Mesh
入力されたメッシュ（M）の面方向を揃えて出力する。
MeshMap
C
Kangaroo2＞Mesh
ソースメッシュ（M1）からターゲットメッシュ（M2）に点（P）をマッピングする。
MeshTurn
C
Kangaroo2＞Mesh
それぞれのメッシュ面の頂点の順序を回転する。
NakedVertices
B
Kangaroo2＞Mesh
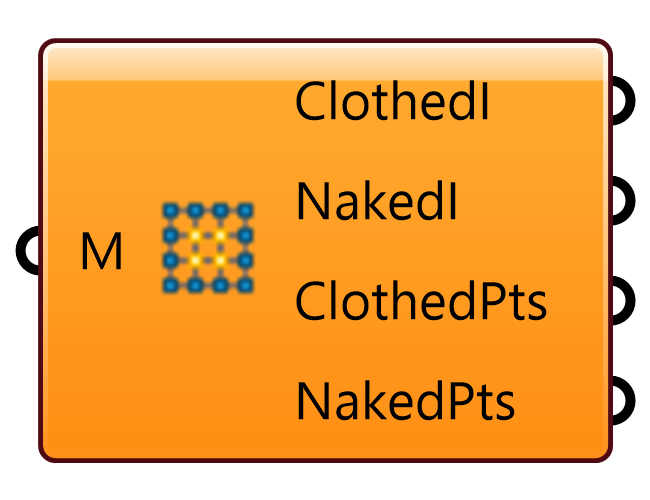
入力されたメッシュ（M）の頂点を端面上に位置するもの（Naked）とそうでないもの（Clothed）に分離し、インデックス（I）と座標（Pts）を出力する。
PlanarityAnalysis
C
Kangaroo2＞Mesh
メッシュのFaceの平面度を分析し、色付けしたメッシュを出力する。完全に平面の場合は黄緑に、平面からのずれに応じて黄、オレンジ、赤と色が変わる。Max（X）で設定した上限値以上の場合に赤となる。
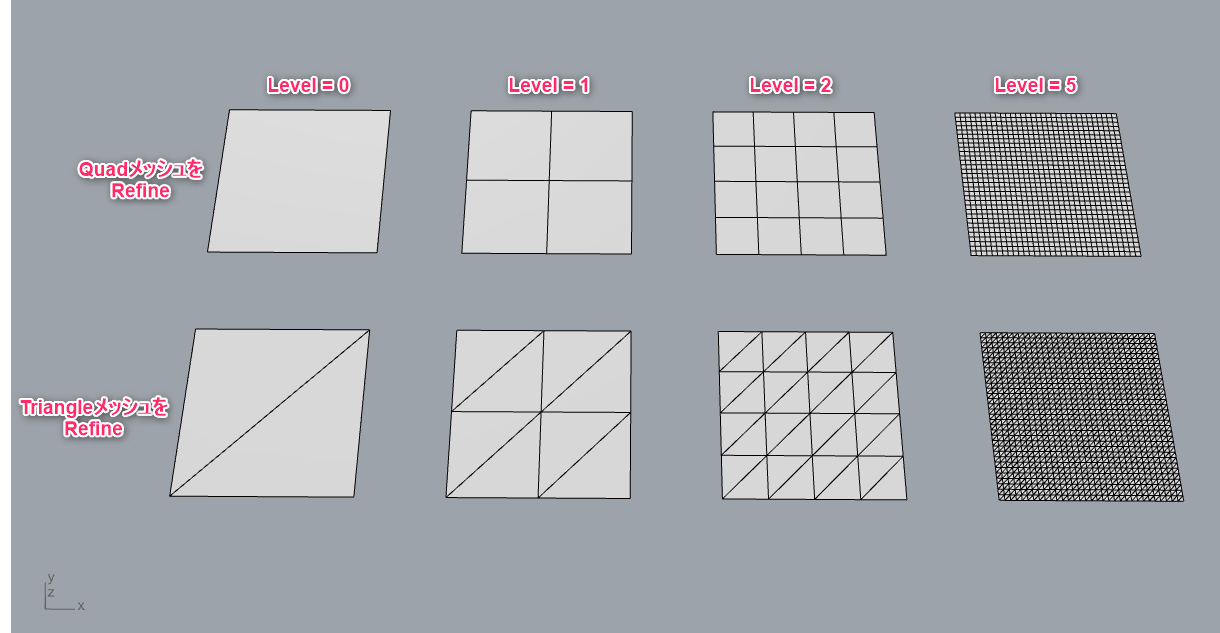
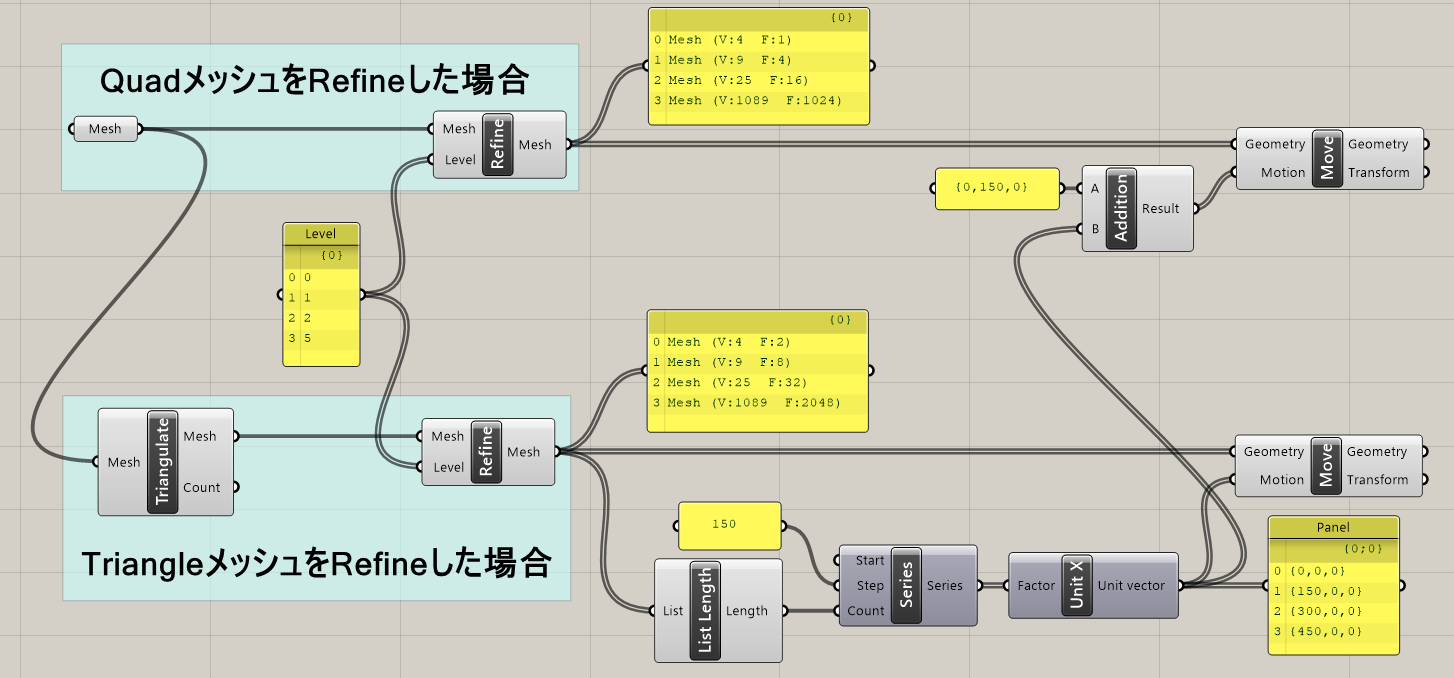
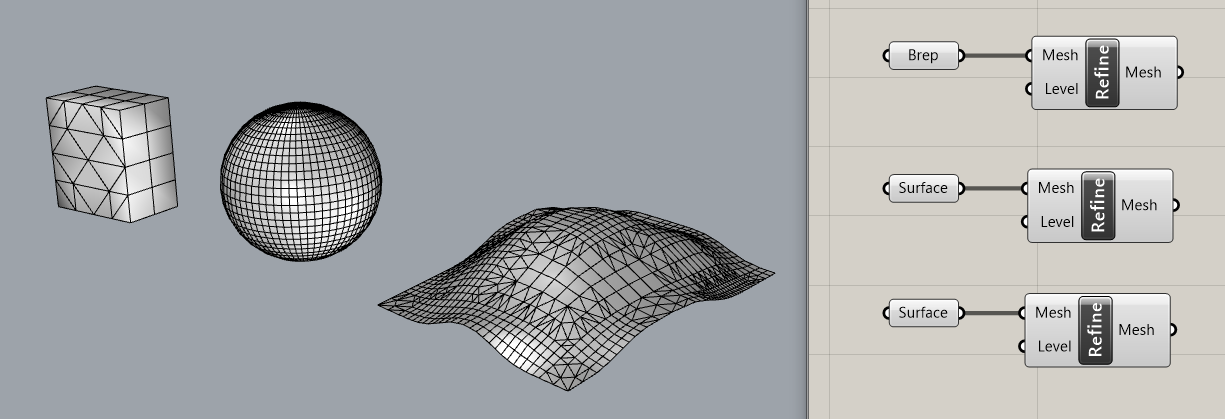
Refine
A
Kangaroo2＞Mesh
入力されたメッシュ（M）内のそれぞれのメッシュをさらに4分割する。四角形メッシュは4つの四角形メッシュに、三角形メッシュは4つの三角形メッシュに分割される。レベル（L）に入力された回数これを繰り返す。
サンプルデータをダウンロードできます
詳細1：[Refine]コンポーネントは、Quad（四角形）メッシュポリゴンやTriangle（三角形）メッシュポリゴンをそれぞれ4分割する（下図参照）。分割の繰り返し数がLevel入力で設定可能だが、4のn乗でメッシュ数が増えるのであまり大きいLevel値を設定すると動作が遅くなるので注意が必要だ。例えば、Level値＝５でも1024倍のメッシュ数となる。
詳細2：Mesh入力端子への接続は、下図のようにメッシュでなくても良い。ポリサーフェスやサーフェスなどのジオメトリを繋いでもメッシュに変換し、Refineした結果を出力する。
RefineStrips
C
Kangaroo2＞Mesh
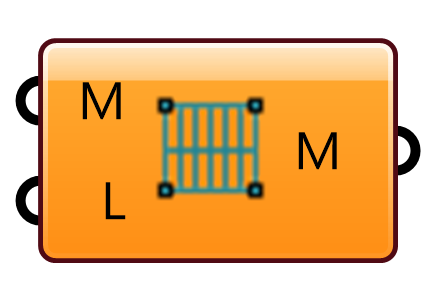
入力されたメッシュ（M）のそれぞれの四角形メッシュを一方向のみ分割する。分割数はレベル（L）で指定する。
RemeshByColour
C
Kangaroo2＞Mesh
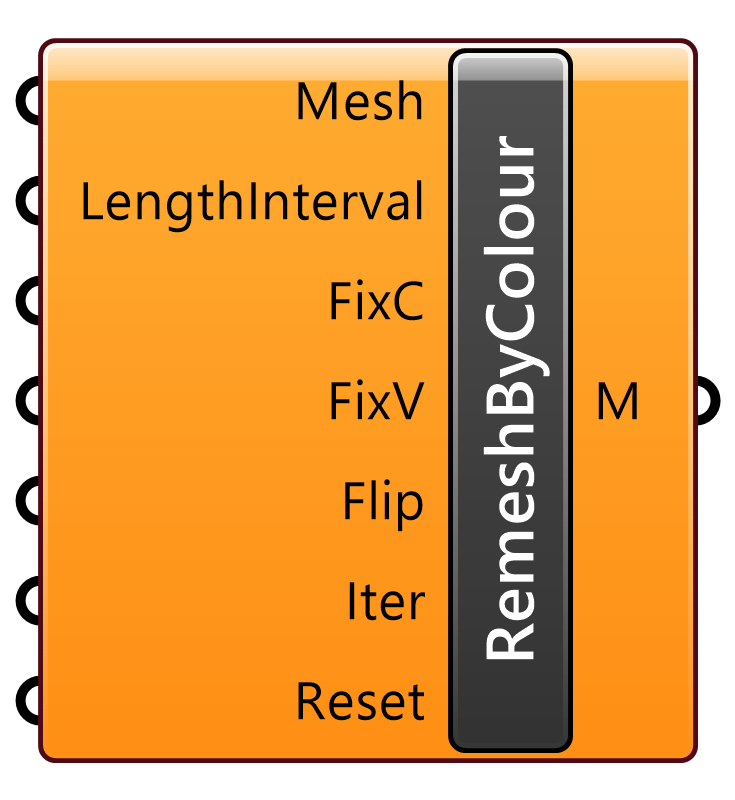
入力されたメッシュ（Mesh）の頂点の色データに応じてエッジ長さを決め、メッシュを再生成する。
SimpleRemesh
C
Kangaroo2＞Mesh
目標とするエッジ長さ（Length）や保持したい曲線（Creases）、点（Corners）を指定し、メッシュを再生成する。Rhino7までのコンポーネント。
Stripper
C
Kangaroo2＞Mesh
入力されたメッシュ（M）をV方向のエッジで分割する。
TangentCircles
C
Kangaroo2＞Mesh
入力されたメッシュ（M）のそれぞれのメッシュの内接円（I）、頂点を中心としたサークルパッキング円（C）、内接円の中心を頂点としたメッシュ群（D）を出力する。
Unroller
C
Kangaroo2＞Mesh
入力されたメッシュ（M）をV方向に展開する。メッシュはStripperコンポーネント等でV方向に分割されている必要がある。展開する量（T）は0～１で指定し、0で元の状態、１で完全に展開された状態となる。
VertexNeighbours
C
Kangaroo2＞Mesh
メッシュ（M）と頂点の番号（V）を入力し、頂点座標（C）とそれと隣接する頂点の座標（N）、その法線ベクトル（V）を抽出する。
WarpWeft
B
Kangaroo2＞Mesh
入力されたメッシュ（M）を縦糸（A）と横糸（B）の2つのリストに分ける。
Utility
DotDisplay
C
Kangaroo2＞Utility
入力した点（P）を水色のドットで表示するコンポーネント。
interconnectPoints
C
Kangaroo2＞Utility
入力された点（P）を端点としたすべての組み合わせの直線を生成するコンポーネント。
Möbius Transformation
C
Kangaroo2＞Utility
入力されたジオメトリ（G）をメビウス変換を使用して変形するコンポーネント。
removeDuplicatelines
B
Kangaroo2＞Utility
入力された直線（L）のうち、設定した許容差（t）内に収まる直線を削除するコンポーネント。
removeDuplicatePts
B
Kangaroo2＞Utility
入力された点（P）のうち、設定した許容差（t）内に収まる点を削除するコンポーネント。
SplitAtCorners
B
Kangaroo2＞Utility
ポリライン（P）とコーナーを定義する角度（A）を入力し、コーナー点（C）と分離したポリライン（S）を抽出するコンポーネント。