[ ビギナーのための曲面モデリングセミナーTop | 予告編 | 第1回 | 第2回 | 第3回 | 第4回 | 第5回 ]
第3回 トリム曲面|本当は4角形の曲面を輪郭に沿って切り取るしくみ
エッシャーの不思議画とドッジボールコート
エッシャーという人がおりまして、とても不思議な画を描いています。
どこまで上ってもてっぺんにたどり着かない階段やいつまでも枯れない水の流れ、魚がだんだん鳥に変わっていくグラデーション模様などが有名です。
一種のだまし画です。幾何的に緻密な計算をして描かれた画であります。
だまされるしくみは、錯覚です。
3次元空間に広がる風景や配置されたものをキャンパスや写真など2次元の世界に映し込んでも、それを見た人間は3次元空間に広がる様子をイメージすることができます。
イメージするために脳のどこかが頑張っているわけです。
見慣れた2次元パターンなら問題なく3次元の世界に展開できます。見慣れたパターンを少しだけ崩すとイメージした3次元世界であれ?ということになるのですね。

今回のテーマは、トリム曲面です。パラメトリック曲面は、基本的にハンカチを広げたような4辺形でしかありません。適当な輪郭(線)を与えて不要部分を切り取ると(トリムすると)5角形や6角形のハンカチを作ることができます。
この輪郭線を与えるしくみについて説明していきます。3次元空間に浮かんだ曲面の上にドッジボールのコートの作るとします。曲面上でしか動けない選手にとって、自分が立っている場所が3次元空間のどこかというより、曲面上のどこかという認識のほうが大事ですよね。「あっ!」「線踏んだ!」というふうにコートの内か外かを区別することが重要になります。
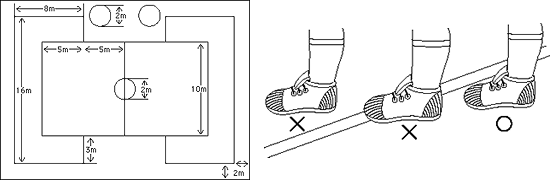
「曲面上に拘束されている」という条件を付けると、3次元の世界を2次元の世界で考えることができます。
これからの説明は、3次元の世界と2次元の世界を行ったり来たりします。だまされない様に読み進めてください。
*紹介したエッシャーの画
/AscendingDescending/HouseOfStairs/WaterFall/MebiusStrip2/SkyAndWater
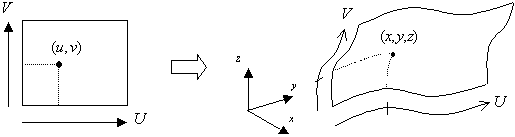
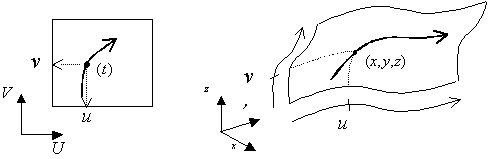
UV空間からxyz空間への写像
(第1回:パラメトリック曲線・曲面参照)
まずは、パラメトリック曲面についておさらいしておきます。
1組のパラメータ(u,v)が与えられた時、点(x,y,z)が対応するしくみを作ります。u、vをある範囲で独立して変化させると対応する点(を集めたもの)は面状に広がる雲になります。
この雲が曲面を表します。パラメータ(u,v)から点(x,y,z)を対応するしくみを「写像(マッピング)」と呼びます。
この写像を利用して作った曲面を「パラメトリック曲面」と呼びます。
パラメータuとvが存在する世界は、独立した2個の変数が支配する(2次元)空間です。
ここでは、この世界を「UV空間(ユーブイくうかん)」と呼ぶことにします。
点(x,y,z)が存在する空間は「xyz空間」と呼ぶことにします。(分かりやすいでしょ!)
参考書によっては、UV空間を「(2次元)パラメータ空間」、xyz空間を「現実(real)空間」とか「オブジェクト空間」と記述したものもあります。
曲面には裏と表がある
パラメトリック曲面は、縦糸と横糸が編み込まれた布みたいなものです。
横糸は横糸で、縦糸は縦糸で全て同じ向きになっています。
曲面上の任意の位置で縦糸と横糸の走る方向をチェックします。右手でフレミングの法則を示してください。横糸の方向を親指、縦糸の方向を人差し指とすると中指の指す方向が曲面の表になります。(これは一般的な定義方法です。もちろん、例外もあります)
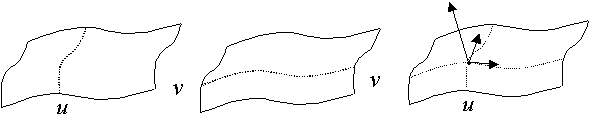
曲面上に線を引く:UV曲線
ハンカチを5角形にしてみます。
とりあえず4辺形のハンカチの上に切り取るための輪郭線を引く必要があります。
輪郭線を針金で作ってハンカチに乗せてみるのも手です。
ハンカチと針金の間に隙間があると輪郭がどこかはっきりしません。だからこんな隙間はあってはなりません。ハンカチが平らなら針金はきちんとハンカチの上に隙間なく乗せることができます。
3次元空間にふんわり浮かんだハンカチならどうでしょう。ふんわり加減に応じて針金をぴったりハンカチに沿わせるのは至難の技ですね。
3Dモデリングの世界では、ハンカチ(曲面)をトリムするために輪郭線として針金(3次元空間に定義された曲線)を用いるのは諦めました。
で、どうしたかというと「輪郭線はUV空間で引く」ことにしました。
パラメトリック曲面の面白い性質です。UV空間は2次元の世界です。つまり平面!UV平面の上に引かれた輪郭線は、写像によってxyz空間に展開することができます。
この輪郭線は3次元空間でも間違いなく曲面の上に乗っています。
全く曖昧さがありません。
このように、曲面を定義するために利用していた「UV空間に曲線を引く」ことを考えます。
この曲線を「UV曲線」とか「パラメータ空間曲線」と呼びます。UV曲線は曲面をトリムするための輪郭線として利用されます。
UV曲線もパラメトリック曲線です。パラメータtを指定すると点(u,v)が対応づけられます。パラメトリック曲線、パラメトリック曲面の性質に注目すると、次の手順でパラメータtから曲面上の点(x,y,z)が求められます。
(t)-> 写像:UV曲線 -> (u,v) -> 写像:曲面 -> (x,y,z)
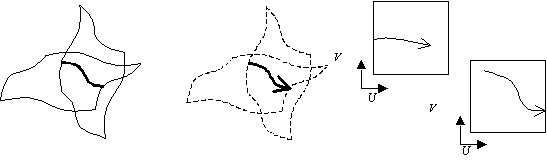
UV曲線は、曲面上の曲線を表します。2つの曲面の交差を考えてみましょう。 一般に交差は曲線(交線)になります。交線は、2つの曲面のどちらの上にも乗っています。 幾何計算で2曲面の交差を求めると、計算結果として3つの曲線が得られます。3次元空間に浮かぶ普通の曲線、一方の曲面のUV空間で定義される曲線、もう一方の曲面のUV空間で定義される曲線 ですね。
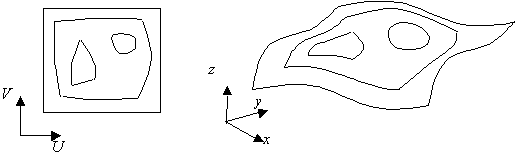
トリム曲面のデータ構造
輪郭線は、一筆書きになる複数の曲線から定義されます。 一筆書きになった複数の曲線を「ループ(LOOP)」と呼びます。この一筆書きは必ず閉じています。(だからループなのですが)トリム曲面は、必ず外周を表す輪郭を持ちます。内側に穴を表す輪郭を持つこともできます。それぞれの輪郭をあらわすループを「アウターループ」、「インナーループ」と呼びます。「ループ」を構成する曲線を「エッジ(EDGE)」と呼びます。
トリム曲面は、1個の(ベース)曲面、1個のアウターループ、0個以上のインナーループから構成されます。各ループは1個以上のエッジから構成されます。(ベース曲面が円筒面や球面などの場合、アウターループとインナーループの区別ができなるケースがあります。)ベース曲面はパラメトリック曲面、エッジはUV(パラメトリック)曲線として表されます。
トリム曲面から、輪郭を表すループ情報を捨て去ることを「トリム解除(アントリム)」と呼びます。こうなると普通の(4辺形の)曲面になります。
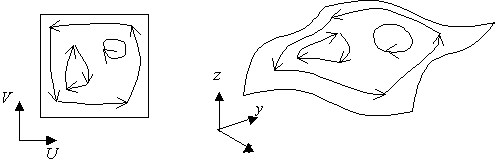
輪郭線のどちらが有効か?
トリム曲面の有効な領域は、アウターループの内側で、かつインナーループの外側です。ところが、アウターループもインナーループもエッジを順番に一筆書きに並べただけで、データ構造からは区別がつきません。(アウターループとインナーループの区別すらできないケースもあります)この曖昧さをなくすため、ループには「向き」が与えられています。UV空間にアウターループとインナーループを作ってみます。アウターループは「反時計回り」、インナーループは「時計回り」の向きをもつことにします。あなたがループに沿って歩くとき、トリム曲面の有効領域は常にあなたの左側にありますね。xyz空間に広がる曲面でも同様の考えが成り立ちます。曲面の表を上にして、ループの向きに沿って歩くとき、トリム曲面の有効な領域は常にあなたの左側にあります。
トリム曲面の表示
CRT(液晶ディスプレイ全盛では死語になりそうですね)に曲面を表示するのは、結構大変です。「アイソパラメトリック曲線」を複数ならべて「メッシュ」にしてみたり、曲面表面を小さな3角形(これを「ファセット」と呼びます)で埋めたりして曲面を象徴します。トリム曲面ではどうでしょう。曲面の仲間ですからやはりメッシュやファセットを用います。ただし、輪郭からはみ出した部分は表示しません。事前にアイソパラメトリック曲線やファセットが有効領域にあるかどうかチェックする処理を施してあります。有効領域内にだけアイソパラメトリック曲線やファセットを生成するという表現もできるでしょう。
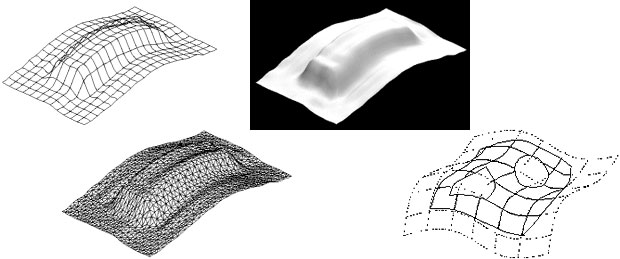
ライノセラスのトリム曲面
ライノセラスでは、Trimコマンドで曲面をトリムすることができます。輪郭線は、曲面上にある(普通の)曲線や、サーフェス/ポリサーフェスとの交線をエッジとして与えます。操作からは、輪郭線がループになっていないように見えますが、プログラム内部で曲面最外周にエッジを追加生成し一筆書きを完成させています。
エッジはUV曲線として表現されます。交線がUV曲線になることは先に触れました。ほぼ隙間なく曲面上に乗っている(普通の)曲線も
プログラムが内部でUV曲線に変換します。こうしてエッジとして利用できるようにしています。
Splitコマンドは、曲面上の曲線(普通の曲線や交線)を利用して2つのトリム曲面を定義しています。同じ曲面上に2つのアウターループを作っていることになります。

こんなトリム曲面は作っちゃだめ
ほとんどのモデラーで、UV曲線そのものを直接作成することはできません。トリム曲面を作成するためには、ベースとなる曲面と、普通の曲線/交線などでできた輪郭線を指定します。本当の輪郭線としてのUV曲線は内部で自動的に生成されます。トリム曲面の定義としては、「始めにUV空間に輪郭ありき」なのですが、実際にはxyz空間の輪郭線からUV空間の輪郭線を作成するケースが圧倒的です。できたUV曲線が下記のようにならないよう、xyz空間の輪郭線の指定に注意する必要があります。
1. エッジ間に隙間やオーバーラップのあるループ
隣接するエッジは端点が一致しているはずです。100分の1mmとか1000分の1mmというオーダーではそうなっていないケースも多々あります。
2. 自己交差するループ
1つのループが自己交差すると、例えば8の字形状になります。ループに沿って歩くとき左手にトリム曲面の領域があるはずですが、領域が半無限になってしまいます。
3. 交差する複数のループ
アウターループとインナーループ、あるいはインナーループどうしで交差してしまうとトリム領域の指定が曖昧になってしまいます。
4. エッジの接続部が極端な鋭角になっている
トリム曲面を表示するために、有効部分のアイソパラメトリック曲線やファセットを計算する処理が容易に失敗します。
5. 輪郭線が曲面から浮いている
曲面上にあるはずの(普通の)曲線が、曲面から離れているとUV曲線の作成が曖昧になってきます。その結果、隣接するエッジ間に隙間が生じたり、自己交差するループを作ってしまうことになります。
6. 折れたベース曲面
ベース曲面は、滑らかであることが期待されます。折れた部分があってはなりません。一部のシステムで折れた曲面からトリム曲面を作成できるものがありますが、これは異端児です。このようなケースでは、折れた部分で2つの曲面に分割し、それぞれにトリム曲面を作成します。

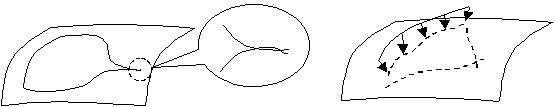

例によって感想質問の連絡先
このセミナーのページで掲載した概念、文章、挿し絵など一切の責任は、筆者にあります。
質問、意見は筆者まで。決してアプリクラフト社へはねじ込まないでください。
株式会社エムシースクウェアド 代表 大野敏則
TEL:053-450-7266 FAX:053-450-7288
info@mc-squared.co.jp
【参考文献】
・Rhinoceros バージョン1.0 ユーザーガイド 19章
・3次元CADの基礎と応用
千代倉、鳥谷、共立出版、ISBN4-320-02539-3
・ CAD/CAMにおける曲線曲面モデリング
穂坂 衛、東京電気大学出版局、ISBN4-501-52250-X
・ コンピュータディスプレイによる形状処理工学 Ⅰ
山口富士夫、日刊工業新聞社、ISBN4-526-01434-6
[ ビギナーのための曲面モデリングセミナーTop | 予告編 | 第1回 | 第2回 | 第3回 | 第4回 | 第5回 ]
