このページは、最適な入力値を調べる – Galapagosコンポーネントについての内容を書いています。
“遺伝的アルゴリズム”や”焼きなまし法”といったソルバで最適な入力値を求めることができます。
- [Galapagos]コンポーネントの使用方法を知りたい方へ
- Grasshopperアルゴリズム上で最適値を求めたい時に
- Grasshopper応用
- 自動的に最適値を計算してくれる
- プラグイン不要
- “遺伝的アルゴリズム”や”焼きなまし法”により、時間と共に最適な入力値を求めることができます
[Galapagos]コンポーネントを使うことで、”遺伝的アルゴリズム”や”焼きなまし法”といったソルバ(英:Solver)で結果が最小、もしくは最大となる最適な入力値を求めることができます。結果となる値に”Fitness”(収束)から、入力値となる値に”Genome”(ゲノム 遺伝情報)と呼ばれる端子から繋ぐことで使用します。
[Galapagos]の働きを例えると、親→子供→孫と順に子供を産んでいった時に、孫のテストの成績(Fitness 収束)が一番高くなる親の組み合わせ(Genom 遺伝情報)を探すというような考え方になります。 正しい計算結果を求めるのではなく、最適な値を探すという働きなので、計算時間が進むにつれより適した値を見つけることができます。
※ここで紹介する内容のgh定義ファイルは、下記リンク先の「5-3 Galapagos」章からダウンロード可能です。
https://www.applicraft.com/cpmodeling_data/

また[Galapagos]コンポーネント自体は、値を出力する端子がなく、入力値であるGenomeを変更します。
下のGrasshopperでの例だと、Parameterというスライダ(Genome)によって曲線上の点を取得する。取得した点と任意の点の間に直線を作成し、その直線の長さ(Fitness)が一番短くなるスライダの値を探すということになります。
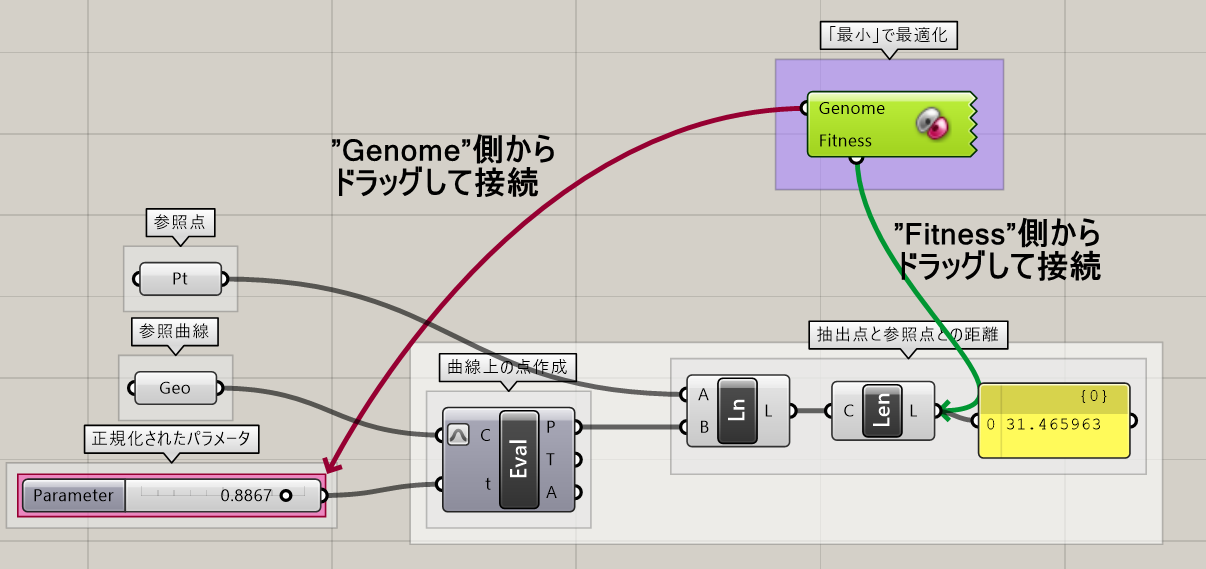
また[Galapagos]を使う際、通常のGrasshopperで作るアルゴリズムそのまま利用することができます。ただし、GrasshopperのUIを使って最適値を探すため、設定によっては望まない答えに陥ることがあります。
一度、[Galapagos]の動作を確認してみます。おおよその流れは下記となります。
1.[Galapagos]を配置し、Genome端子を入力値を探したいスライダなどに、Fitness端子に最大か最小となる収束値を繋ぐ。Genome端子は複数接続も可能。

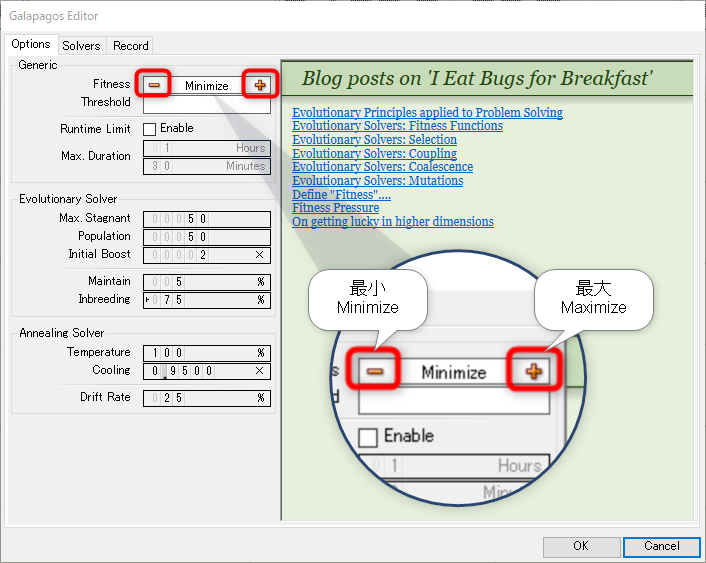
2.[Galapagos]コンポーネントをダブルクリックし、[Galapagos Editor]ダイアログを起動する。[Fitness]を+アイコンもしくは- アイコンをクリックし Maximize(最大)、Minimize(最小)のどちらかに設定する。
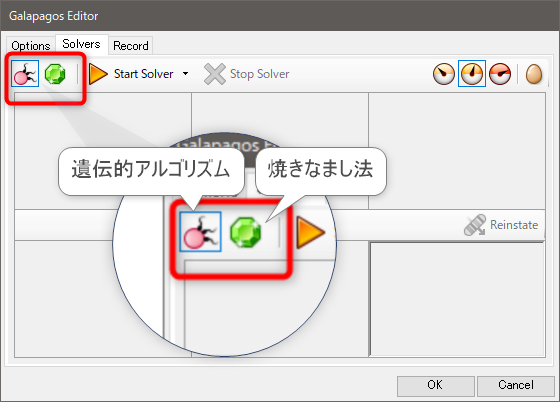
3.Solvers タブに移動し、遺伝的アルゴリズム(左側のアイコン)か焼きなまし法(右側のアイコン)かをクリックし、ソルバを選択する。標準では遺伝的アルゴリズムに設定されている。
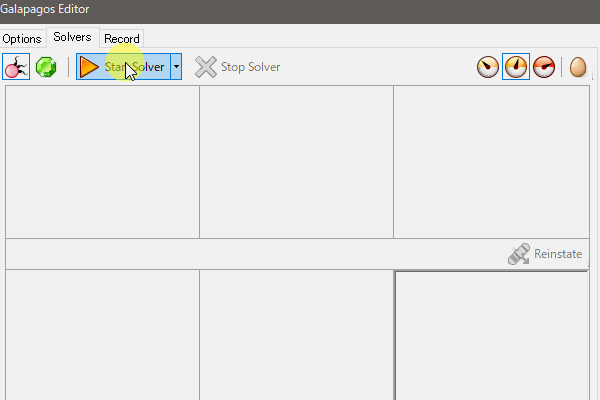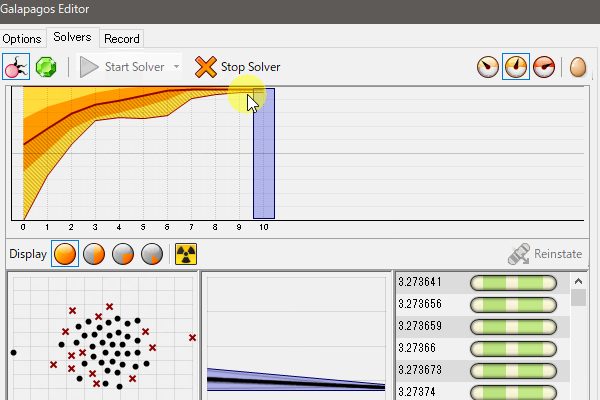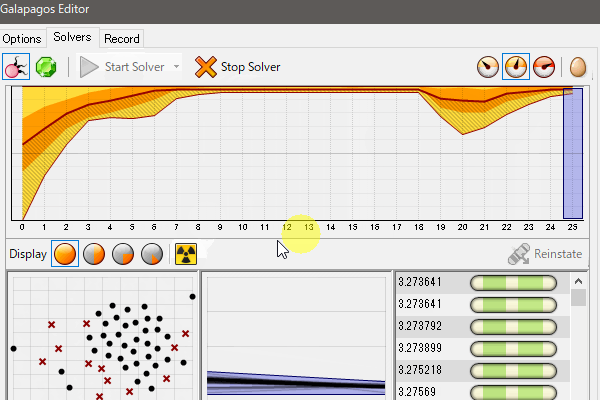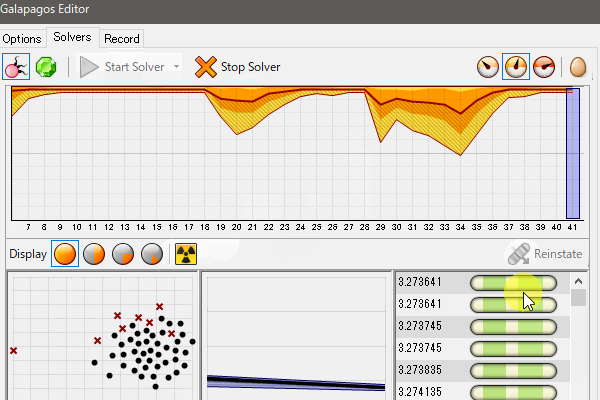
4.[Start Solver]を押し、計算を始める。[Display all genomes in the Rhino viewport]表示にしていると全ての計算結果が、[Only better genomes in the Rhino viewport]では最善の結果が出たときにRhino上の表示が更新される。
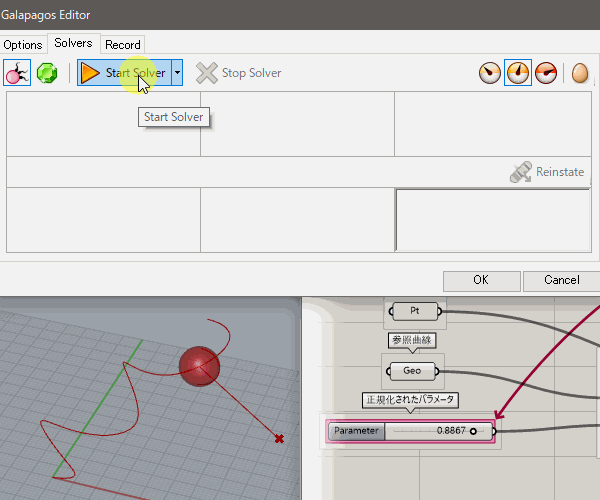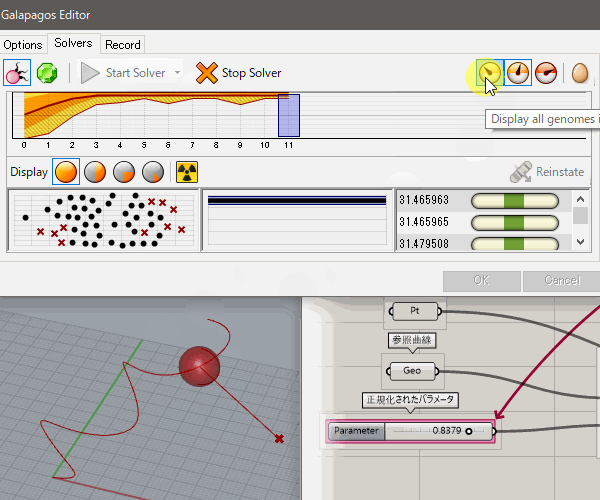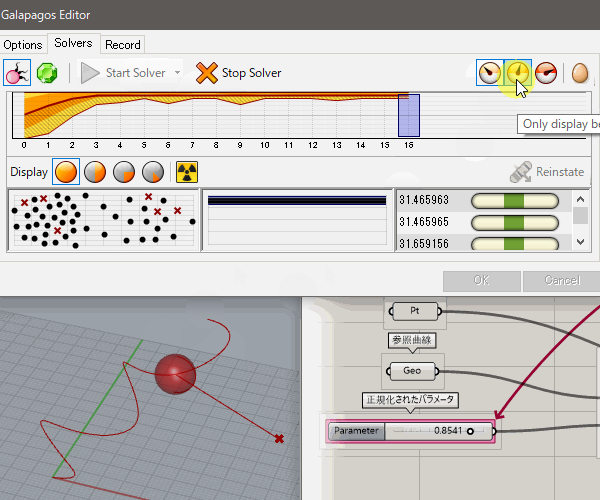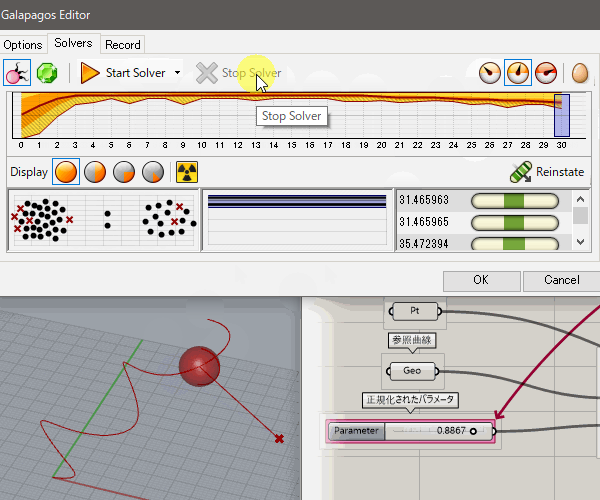
5.計算が進むにつれ、右下に最適な収束値が蓄積されていく。必要なだけ計算が進んだ時点で、[Stop Solver]を押し、計算を止める。
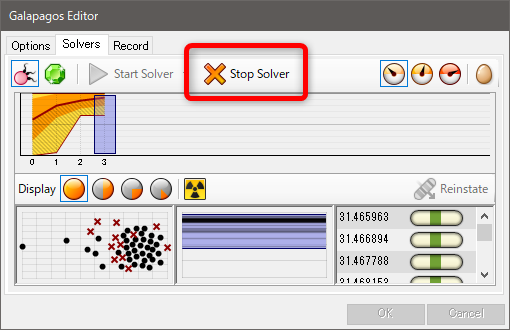
6.特定の収束値をクリックして選択後、[Reinstate]ボタンをクリックし特定のGenome値を選択する。[OK]ボタンを押し、[Galapagos Editor]ダイアログを閉じる。
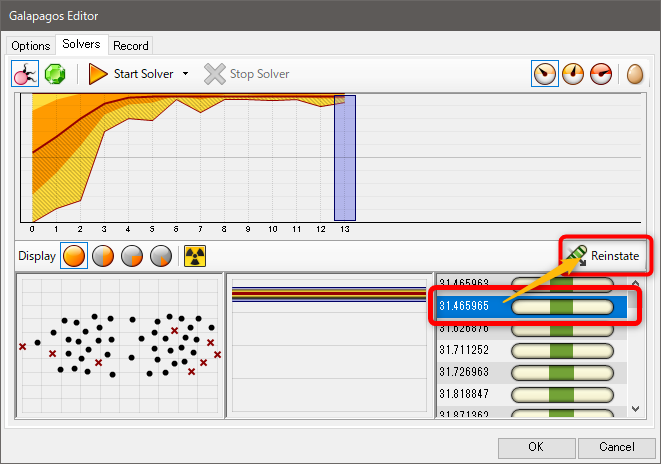
という流れになります。
ここでは[Curve Closest Point]コンポーネントを使って、点から曲線への最近接点を求めています。
[Galapagos]によって求められた長さ31.465963と、[Curve Closest Point]によって求められた長さがほぼ同じ値になっており、[Galapagos]によって最も短い長さとなるGenomeを見つけることができたのが分かります。
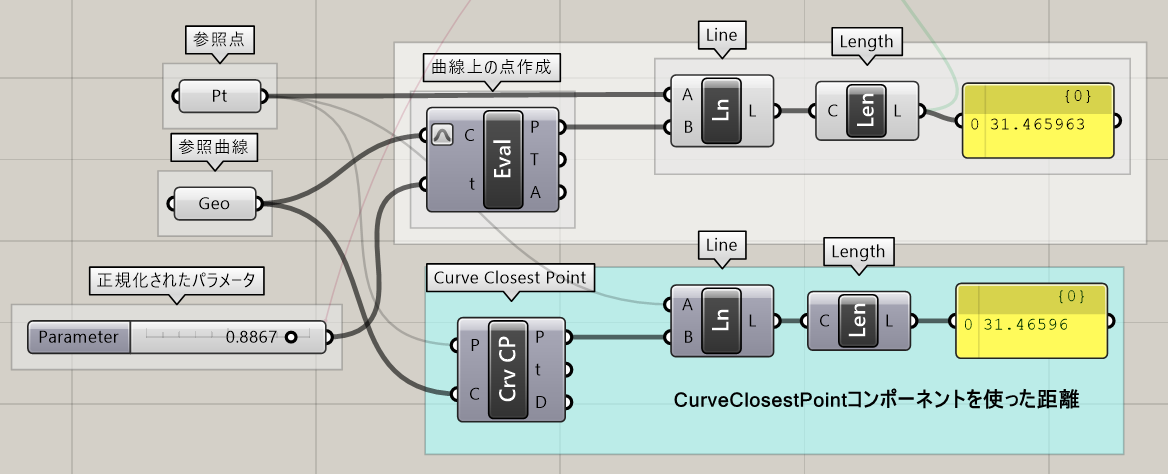
ただし注意する点として、スライダ内のDigits(小数点以下の桁数)の値が少ないと、精度の高い最適値を求めることができません。Parameterと名前の書かれた箇所をダブルクリックして、Slider accuracyの値を適切な値に変更してください。
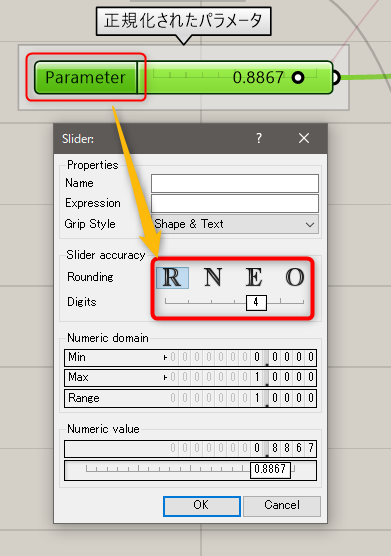
次に、もう少し複雑な[Galapagos]を使わないと、最適な値が見つけづらい例を確認してみます。
平面にある曲線の面積を6等分割する入力値を、[Galapagos]で探してみたいと思います。アルゴリズムの全体像は下記となります(画像をクリックで拡大します)。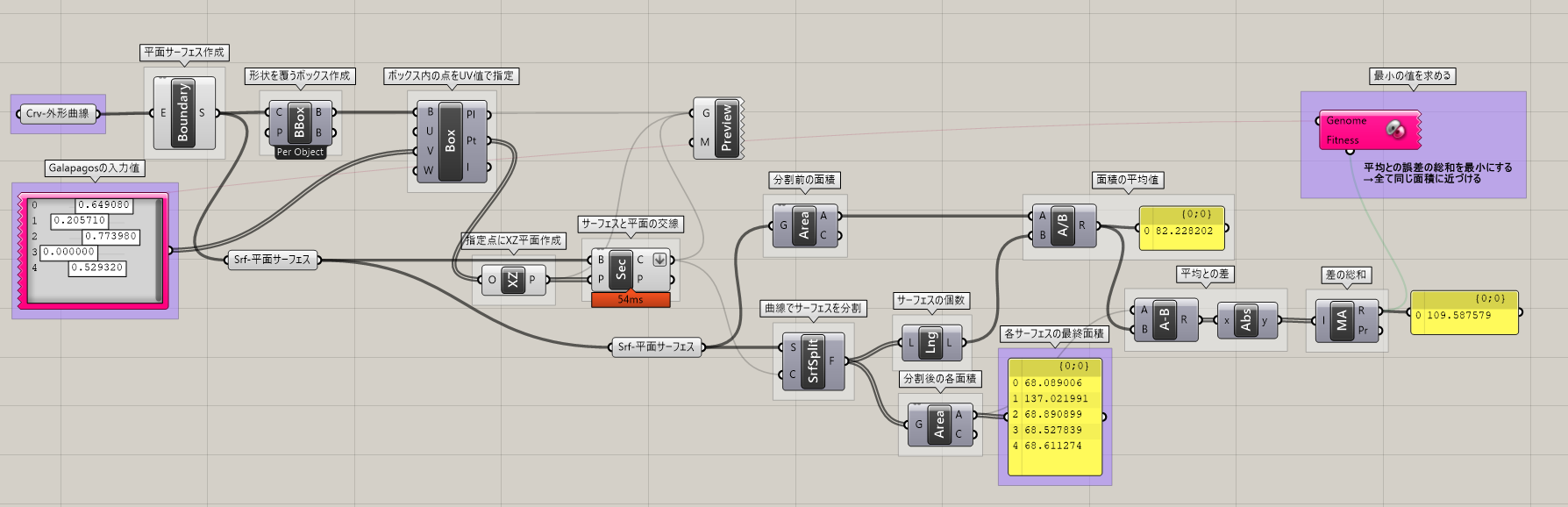
[Galapagos]に入力するGenomeの値を変化させることで、曲線を分割するY方向の位置が変わり、それによりそれぞれの面積が変化します。
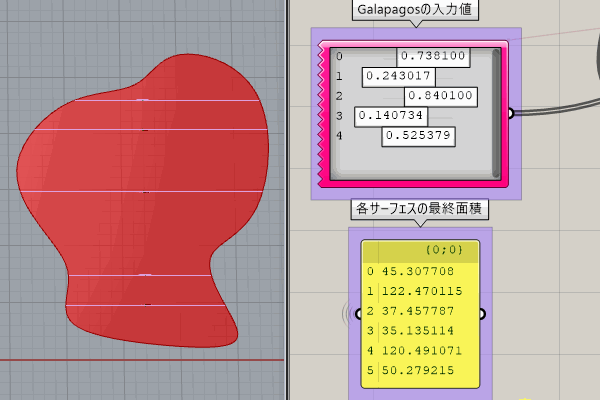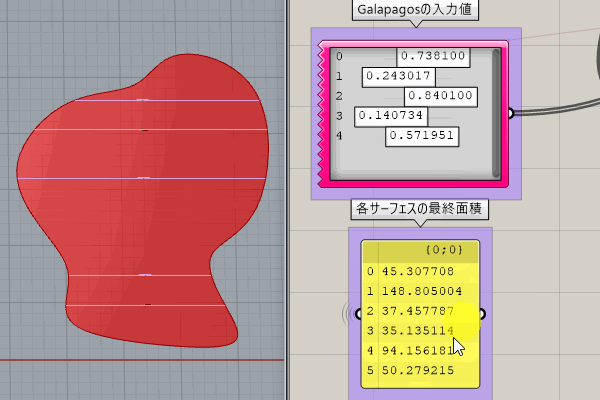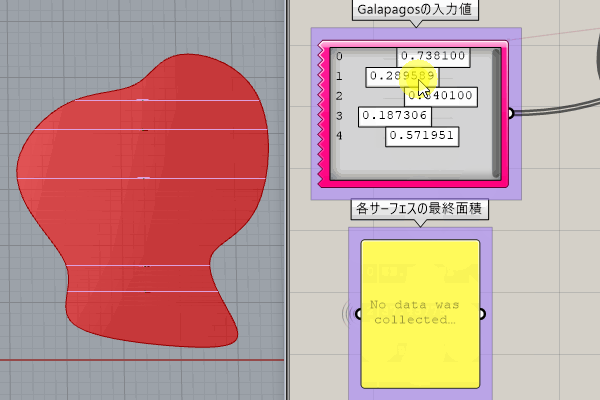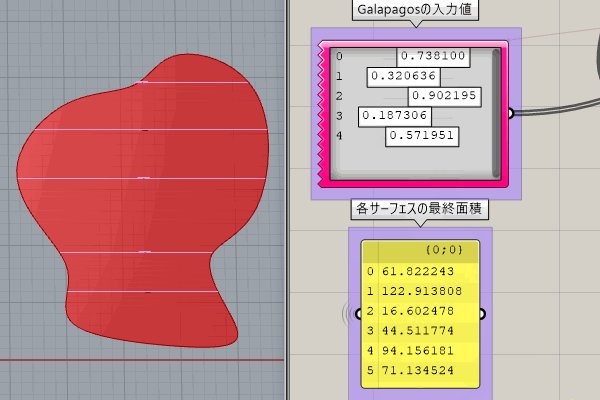
ここでの[Galapagos]を使用する考え方は、下記となります。
1.自由曲線からできたサーフェスの面積をサーフェスの枚数で割り、平均の面積を求める。
2.分割したそれぞれのサーフェスの面積を求める。
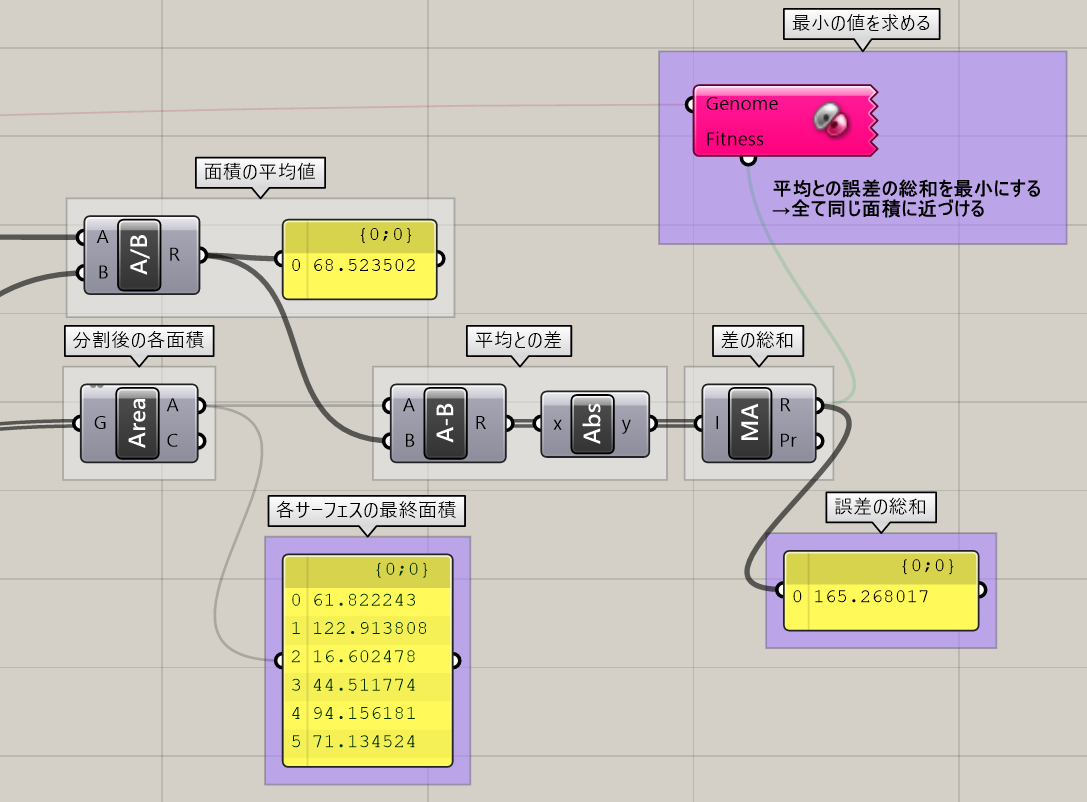
3.1で求めた平均の面積と2との誤差を求めて、誤差の総和を求める。
4.3で求めた誤差の総和を収束値として、Minimize(最小)となる入力値を求める。
というものです。
面積の誤差を最小となる値を探すことで、全ての面積が平均に近づいた値を探すことができます。
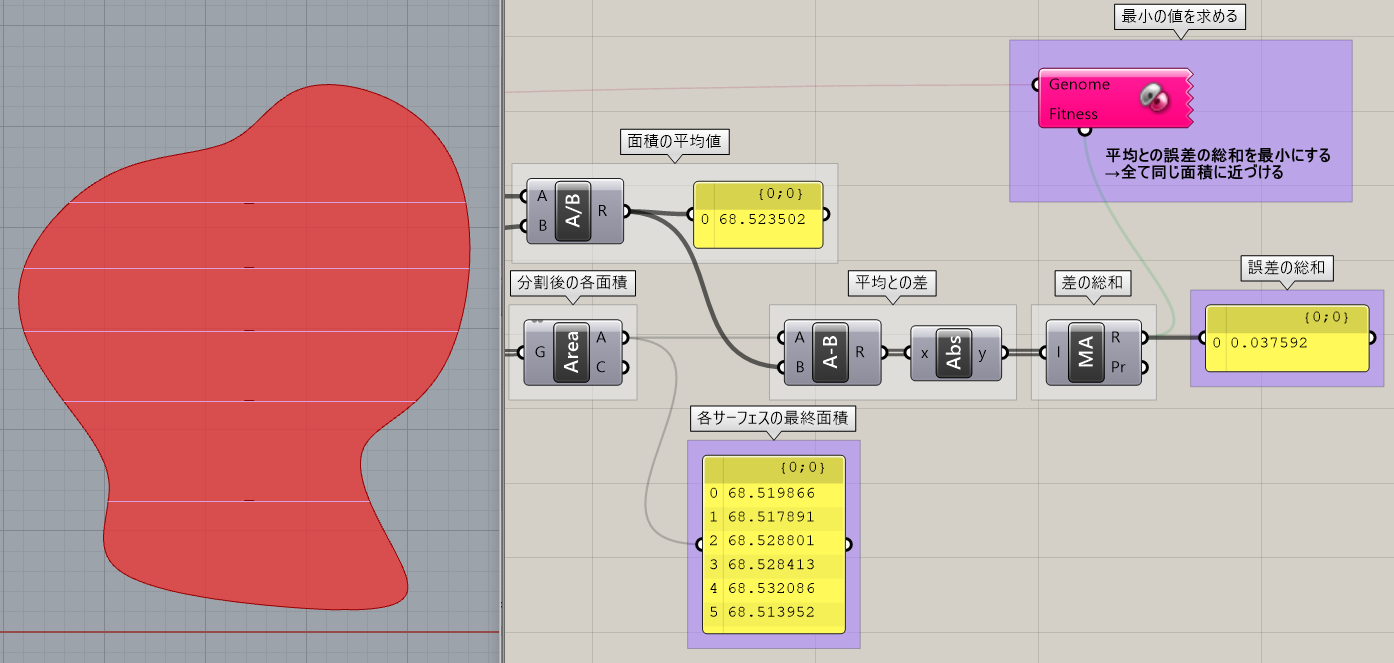
[Galapagos]である程度の回数(30分ほど)、計算したことにより求められた結果の例が下図となります。各サーフェスの面積が68.51から68.53ぐらいに集中し、面積の平均値の68.523とおおよそ近い値が求めることができています。また誤差の総和が0.037592と0に近づいているのも分かります。
次に条件に合わないものを除外しつつ、収束値を探す方法を確認してみます。
下図のように、自由曲線上の任意の3点を入力値として取得し、その3点からできる長方形の面積を最大にする入力値を求めてみたいと思います。
ここでの[Galapagos]を使用する考え方は下記となります。
1.曲線上の3点を取得し、その3点を元にした長方形を作成する。
2.その面積が最大となる入力値を求める。
というものです。
ただし、人間がスライダで値を動かすときは目で見ながら、曲線からはみ出さないように、長方形の位置を設定することができます。[Galapagos]はスライダなどから任意の値を入力するため、曲線からはみ出してしまうことがあります。

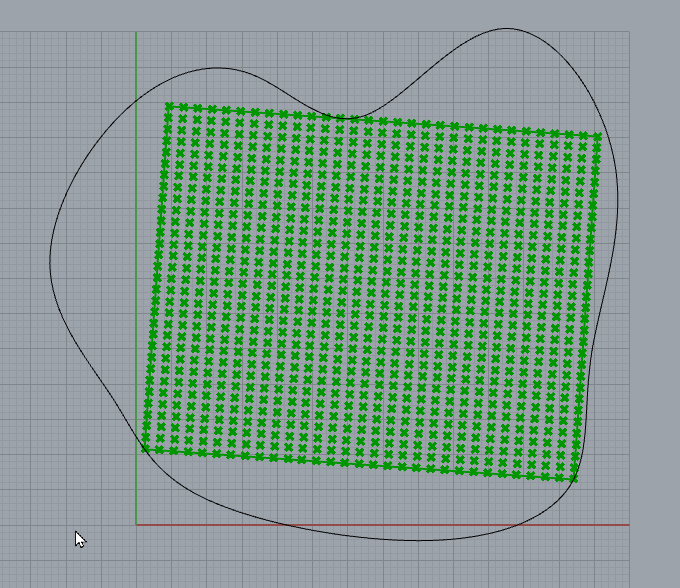
曲線からはみ出た際はペナルティとなる値を与えることで、曲線内に収めつつ面積を最大にする入力値を求めてみます。
ここでは下記の様な考え方で、曲線の外にはみ出したかどうかの判定をしています。
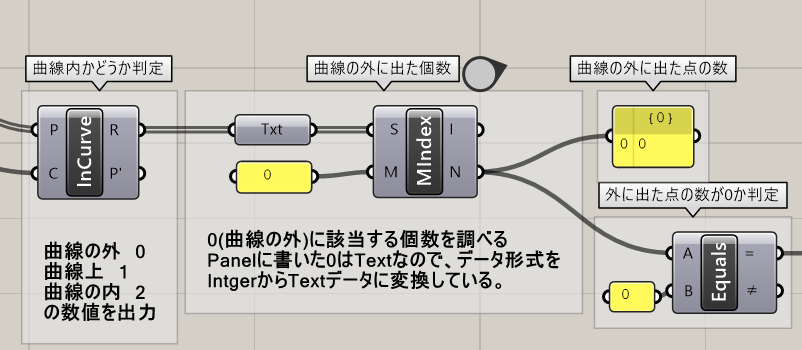
1.[Point In Curve]を使い、四角形に敷き詰めた複数の点がそれぞれ曲線の内側かどうかを調べる。
2.[Member Index]で、曲線の外の点の数を求める。
3.2で求めた曲線の外の点の数が0かどうかを[Equals]コンポーネントで調べて、結果をTrue・Falseで出力する
という流れです。
またGrasshopperでは、Trueは数字で現すと1に、Falseは0で現されます。
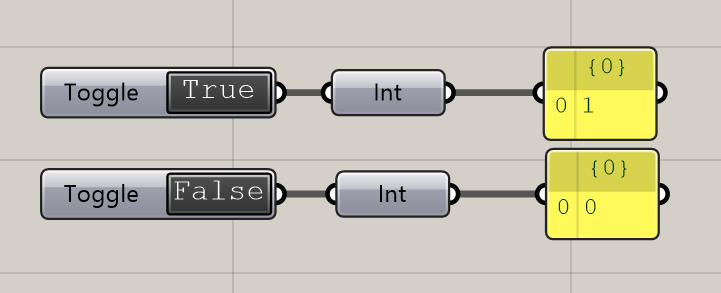
この理屈により、
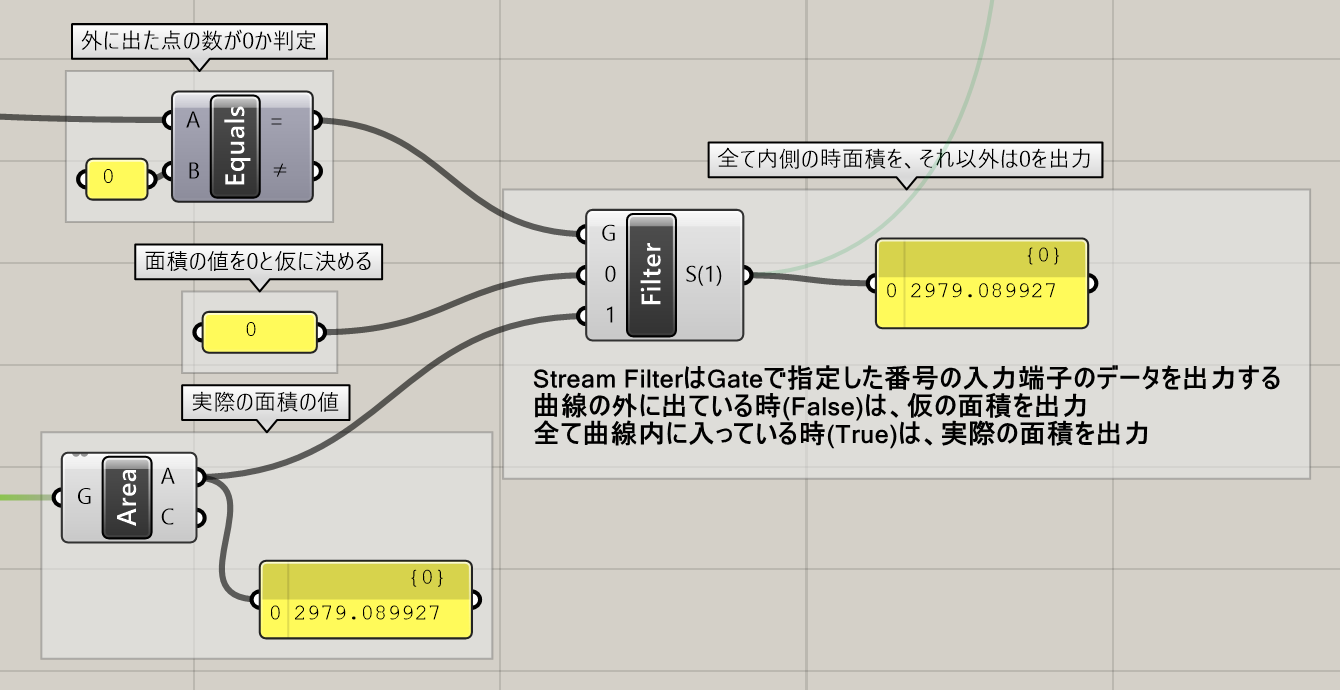
・曲線内に点が全て収まった場合は(True)、[Stream Filter]の1に入力した値を使用する。
・1つでも曲線の外に出た点がある場合は(False)、[Stream Filter]の0に入力した値を使用する。
というアルゴリズムが作成できます。
これにより、条件に満たない時はペナルティとなる値(ここでは低い面積値)を使用することで、曲線からはみ出さないようにしつつ、最大となる面積の個所を探すことができます。
[Galapagos]は、Grasshopperのアルゴリズムが作成できれば、利用することができる応用範囲が非常に大きい機能となります。是非、人力で探すのは難しい最適となる値を求めていただけたらと思います。
補足
望まない解に陥ってしまったときは、Solverで計算実行中に、[Add additional mutations to the population]ボタンを押すことで、収束している値を発散させることもできます。特定の望まない結果に陥ってしまった時は押しても良いかと思います。
また[Galapagos]は、収束値を1つしか持つことができません。より高度な最適値を求めたい場合は、開発元のMcNeel社が運営しているサイト[Food4Rhino]から[Wallacei]や[Octopus]と言ったプラグインを利用することもできます。そちらも是非、ご利用いただけたらと思います。
[Wallacei] https://www.food4rhino.com/app/wallacei-0
[Octopus] https://www.food4rhino.com/app/octopus
