Kangarooは、Daniel Piker氏によって開発されたGrasshopperで物理演算や形状最適化を行うためのプラグインです。
物理的な振る舞いをモデリングに応用できるため、より合理的で自然な形状を模索するのに役立ちます。
ある荷重などの条件に対して合理的な形状を決定する手法は、フォーム・ファインディング(Form-Finding)とも呼ばれます。
Kangarooは、Rhino6からGrasshopperに「Kangaroo2」という名称で標準機能として搭載されました。
Kangaroo2の前身として「KangarooPhysics」というプラグインがありましたが、両者は使用方法が大きく異なります。
- KangarooPhysics → 条件を設定し、時間ステップ毎の解を求める物理シミュレーション
- Kangaroo2 → 各条件に優先順位(Strength)を付け、それらのバランスで解を収束させる手法
ここでは、標準機能として搭載されているKangaroo2について解説します。
Kangarooは、一般的なGrasshopperのコンポーネントとは使い方や特徴が少し異なります。
サンプルなどを通して、まずはその概要をご紹介したいと思います。
どのような形のモデリングに活用できる?
例えば、以下のような形状や物理現象をモデリングに取り入れたいときに役立ちます。
- 懸垂構造(カテナリー)
- 張力構造
- メッシュ最適化
- 極小曲面
- 膨張、収縮
- 衝突、接触
- 布の振る舞い、ドレープ
- 充填(パッキング)
- 剛体、粒子運動、液体
- 梁の振る舞い
- 折り紙
- 結合、アセンブリ、リンク機構
- 特殊な荷重(爆発、風)
頂点やエッジに、荷重や強度、拘束などを条件として与えることで物理的な振る舞いを計算します。
Kangaroo2のサンプルが、Daniel Piker氏のGithubにて公開されていますので、ここではその内のいくつかを分類別にご紹介させていただきます。
※サンプルは、ご利用のRhinoバージョンによって[Grab]コンポーネントが古くなっている可能性があるため、機能しない場合は新しい[Grab]を繋ぎ直してお試しください。
懸垂構造(カテナリー)
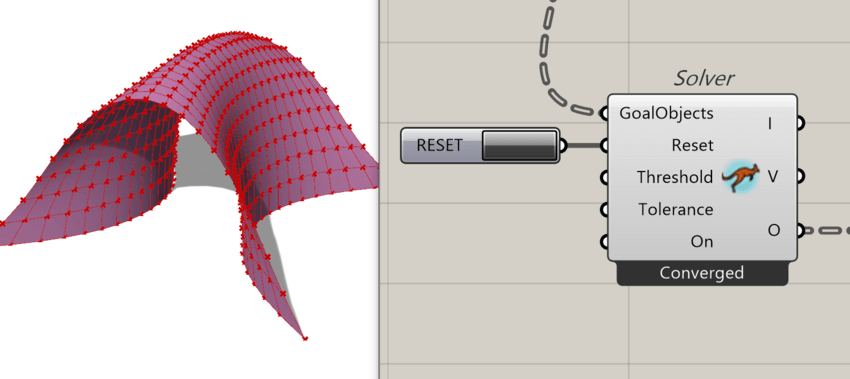
ロープやケーブルを重力方向にたるませた形状をカテナリー曲線と呼びますが、重力の代わりに鉛直上方向に荷重を掛けると図のような形状になります。

上記では、次のような条件を与えて計算を行っています。
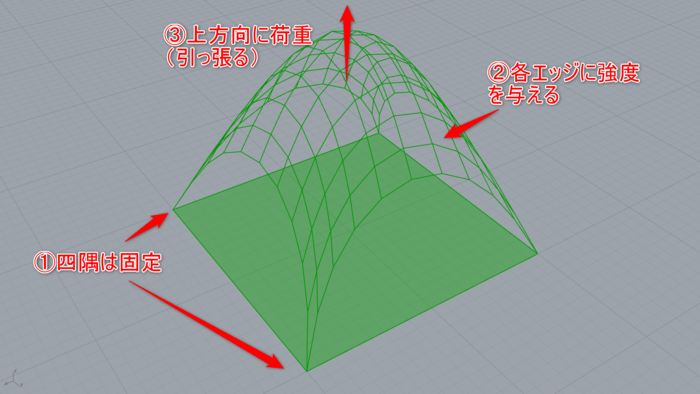
① 四隅の点をその位置に固定する
② メッシュのエッジに強度(弾性)を与える
③ 鉛直上方向に荷重を与える
①が無いとメッシュは上方向へ飛んでいってしまい、②が無いとメッシュはどこまでも伸びてしまいます。③が無いとそもそもメッシュに変形は生じません。
このように複数の条件を与えることでその平衡状態を探索するのがKangaroo2の特徴です。
このときのコンポーネントの組合せは以下のようになっています。
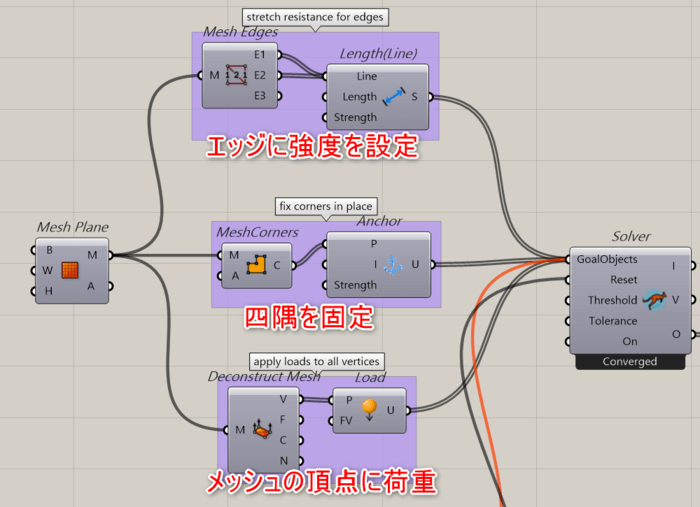
条件を設定するコンポーネントのことを「GoalObject」と呼びます。
上の画像では、[Length(Line)][Anchor][Load]がそれぞれGoalObjectに該当します。
コンポーネントの組み合わせ方の流れについては後半で解説します。
点の拘束条件を少し変えると以下のような形状にもなります。
ここでは両サイドのエッジの頂点を、XY方向の移動は許可、Z方向の移動は禁止にしています。
張力構造
メッシュのエッジに強度を与え、数か所の点を各位置に拘束すると以下のようになります。
テントの幕をポールの先端や地面に固定するイメージですね。

拘束する点を移動すれば、それに合わせて幕形状も追従し、エッジの強度に合わせて形状が一意に決まります。
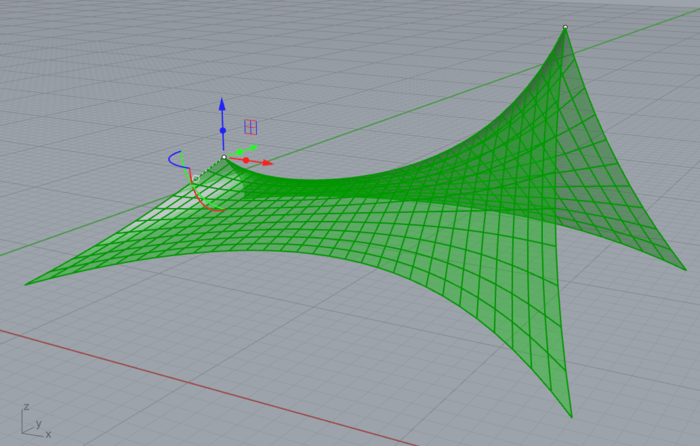
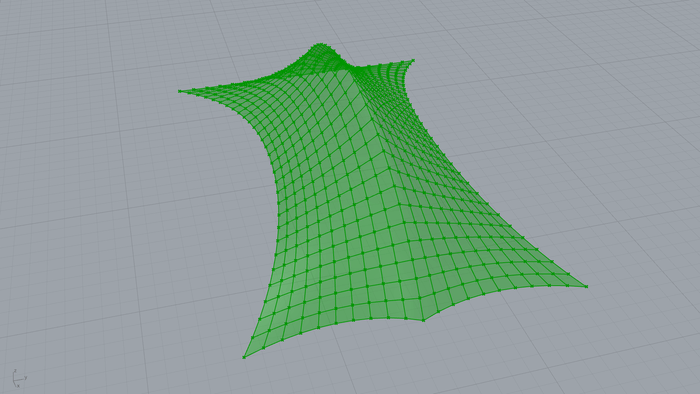
点ではなく、一部の点が曲線の上に乗るような拘束条件を与えると以下のような形状も作れます。
この例ではメッシュの中央の点をアーチ状の曲線上に拘束する条件を設定しています。
メッシュ最適化
このようなエッジの強度により引っ張り合ったり緩んだりする性質を利用すれば、最適なメッシュの構造を探索することにも利用できます。
このような手法は、メッシュ・リラクゼーション(Mesh Relaxation)とも呼ばれます。
極小曲面
以下は、シャボン玉や石鹸膜などに見られる平均曲率がゼロである曲面(=極小曲面)を作成した例です。

膨張、収縮
メッシュの各頂点に法線方向の荷重を設定できます。
正の値なら膨張、負の値なら収縮の振る舞いとなります。

衝突、接触
Kangaroo2では、オブジェクト同士の接触を条件に加えることができます。
以下は、チェーンの例でそれぞれの輪っかには接触条件を与えているためお互いにすり抜けないようになっています。また、Grasshopperのプレビューオブジェクトをマウスのドラッグで動かせる[Grab]という機能が用意されています。
布の振る舞い、ドレープ
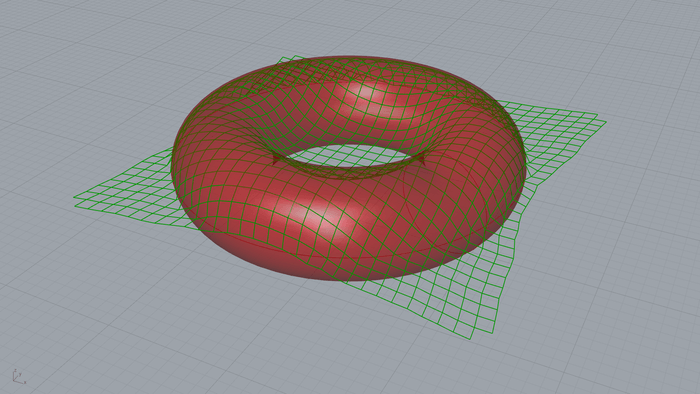
以下も接触の例で、メッシュの面をトーラス状の立体の上に覆い被せた例です。
メッシュには重力方向に荷重が掛かっていますが、メッシュとトーラスおよび作業平面に接触条件が設定されているため、すり抜けず、トーラスに沿ってたるんだ形になっています。
このように布を上から被せたような形状は、ドレープ(Drape)と呼ばれます。
充填(パッキング)
接触を応用すると、ある領域にオブジェクトを充填した形状を探索することができます。特に円を充填した形状やその手法は、サークル・パッキング(Circle Packing)と呼ばれます。
以下の例は、複数の円を曲面上に拘束し、かつ円同士の接触条件を設定した例です。限られた面積の中でお互いの円が押し合いながらできるだけ密になるよう配置されています。
この手法は、スピーカー穴や排気穴の最適な配置を求める場合などにも利用できます。
以下は、画像の濃淡に合わせて円の大きさを調整し、サークルパッキングを行った例です。

剛体、粒子運動、液体
接触の演算時には、任意の立体を変形を許さない剛体として設定することや、半径を指定し球体(=粒子)として設定することができます。
粒子の接触を応用すれば、液体のような振る舞いを擬似的に再現することもできます。
液体の粒子としての振る舞いではなく、波動現象としての振る舞いは、エッジの弾性を利用することで再現できます(参考:Ripple/Raindrop Pattern)。
梁の振る舞い
Kangaroo2では特に設定しない限り、各エッジは軸方向にしか抵抗を持たないトラス要素のように振る舞いますが、曲げやねじれに抵抗を持つビーム要素(梁)として振る舞うような条件を与えることもできます。
端点の支持を並進・回転の6自由度で設定できるGoalObjectも合わせて用いると以下のような挙動が再現できます。
折り紙
ヒンジ(折れ曲がり)を設定するGoalObjectにより、折り紙構造をシミュレートすることができます。
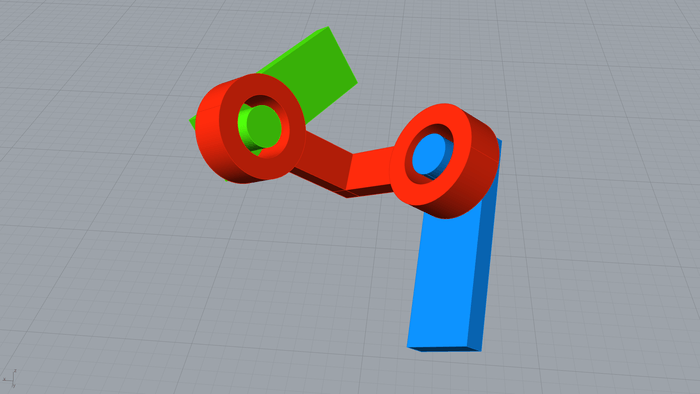
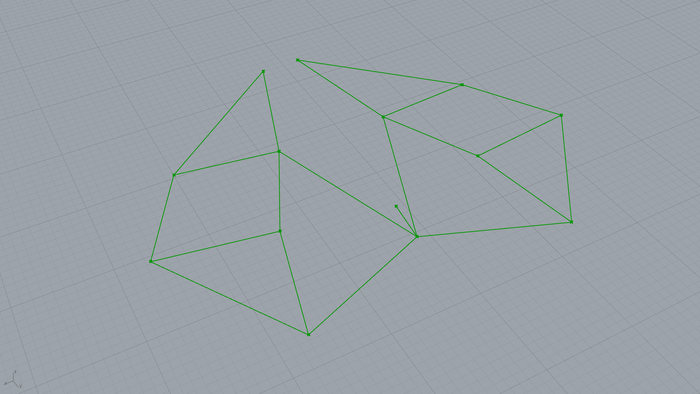
結合、アセンブリ、リンク機構
エッジ同士の接合部の回転軸を設定することで結合やリンク機構、アセンブリのシミュレートが行えます。
特殊な荷重(爆発、風)
1点に全方位に荷重が発生する爆発のような条件や、
風を受けたような荷重を発生させる条件も用意されています。
Kangaroo2の仕組み、構築の流れ
Kangaroo2の機能を利用する場合は、以下の流れでコンポーネントを組み合わせます。
①基本形状を作成
②計算条件を設定(=GoalObject)
③ソルバーでの演算
④結果を抽出
例えば、カテナリーのサンプルで見ると以下のような構成となります。
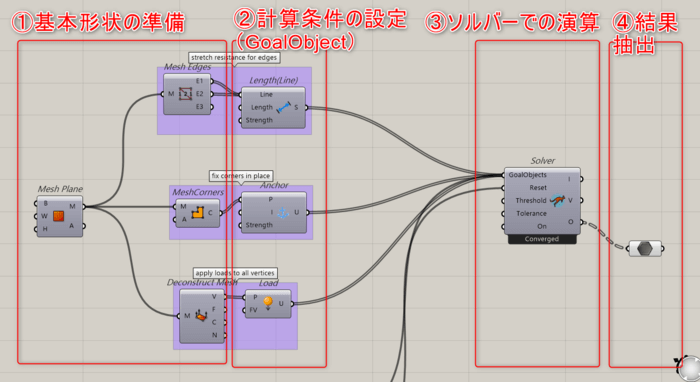
①基本形状の準備 ⇒ 基本形状を準備し、条件を適用するエッジや頂点を抽出します。
②計算条件の設定 ⇒ GoalObjectと呼ばれる計算条件や拘束条件を設定するための専用のコンポーネントに接続します。
③ソルバーでの演算 ⇒ GoalObjectをSolverに集約して接続します。計算をリセットしたり、ストップするための端子が用意されています。
④結果を抽出 ⇒ Solverから出力されたデータの中から、次の工程で使用するものや可視化するものを抽出します。
おおまかには上記のような流れとなります。
多くのGoalObjectは、「Strength」というその条件の優先度(重み付け)を設定する端子を持ちます。
このStrengthによって複数の条件のバランスを考慮し、最適な形状を探索します。
勘違いしやすいのですが、Kangaroo2にはヤング率やポアソン比、反発係数のような単位を持つ具体的な材料定数の設定をする機能はなく、あくまで各条件の重み付けによる相対的な形状の探索となるので、構造解析やCFDのような性能を評価するツールとして用いることはできませんのでご注意ください。
どのようなGoalObjectがある?
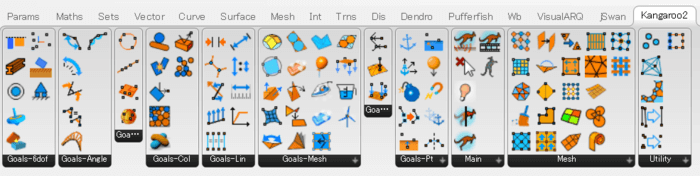
GoalObjectにはたくさんの種類があり、Kangaroo2タブの中でグループ分けされています。
各グループの概要は以下の通りです。
・Goals-6dof … 剛体運動などの6自由度に関する条件
・Goals-Angle … 角度に関する条件
・Goals-Co … オブジェクト間の位置関係に関する条件
・Goals-Col … 接触に関する条件
・Goals-Lin … エッジに関する条件
・Goals-Mesh … 面に関する条件
・Goals-On … オブジェクト上に拘束する条件
・Goals-Pt … 点拘束や点荷重など点に関する条件
・Main … ソルバーなど機能上主要なコンポーネント
・Mesh … メッシュの生成や抽出に関するコンポーネント
・Utility … その他のコンポーネント
各グループ内のそれぞれのコンポーネントの機能の詳細については、GrasshopperコンポーネントIndexのKangarooのページをご参照ください。
Grasshopperコンポーネント:Kangaroo2
今回は、Kanagaroo2の概要についてご紹介しました。
また機会があれば、それぞれの手法についてもう少し詳しく、チュートリアル形式などで解説できたらと思います。
