- Grasshopperの階層構造を理解し、編集を行っている人向け
- Grasshopperを使ってアルゴリズム作成したい人
- Grasshopper応用
- より柔軟にアルゴリズム処理を変化できる
- 少ないコンポーネント数でアルゴリズムを作成
- Grasshopperで階層ごとに処理を変える方法の紹介
このページでは、階層ごとに処理を変えるアルゴリズムを作成する方法を記述しています。
下記の様なグリッド(矩形)状に並んだ点を一筆書きの要領で繋いだポリラインを作成するアルゴリズムを作ってみたいと思います。
その際、
・X,Yの方向のそれぞれの間隔
・X,Y方向に配置するそれぞれの個数
を任意に変更できるよう作成してみます。
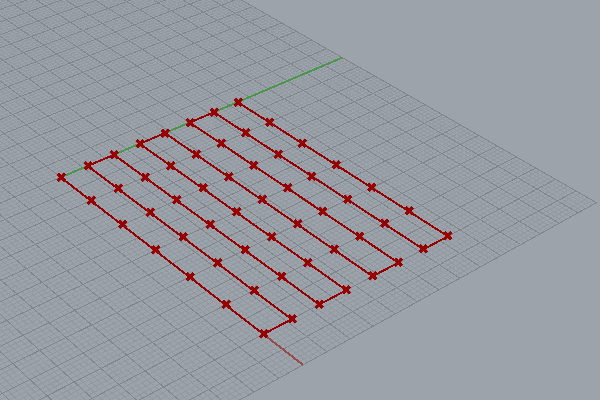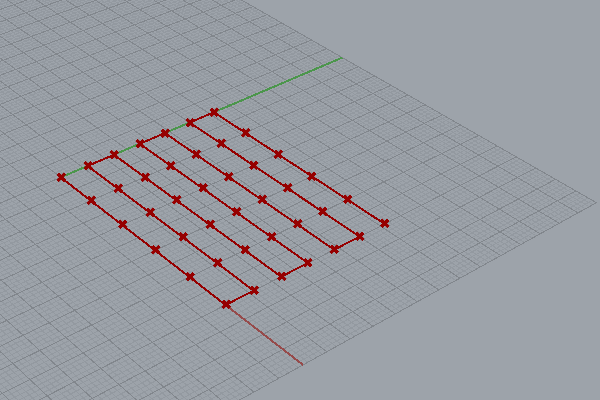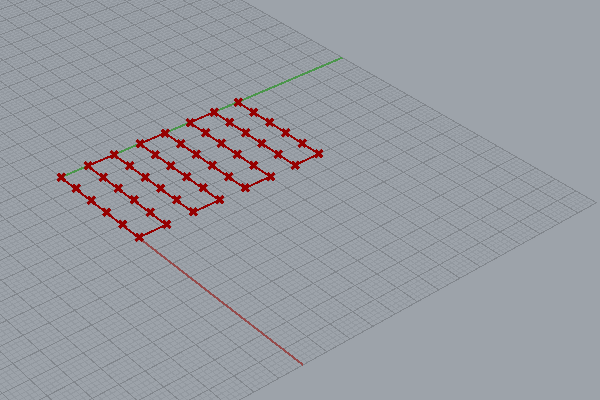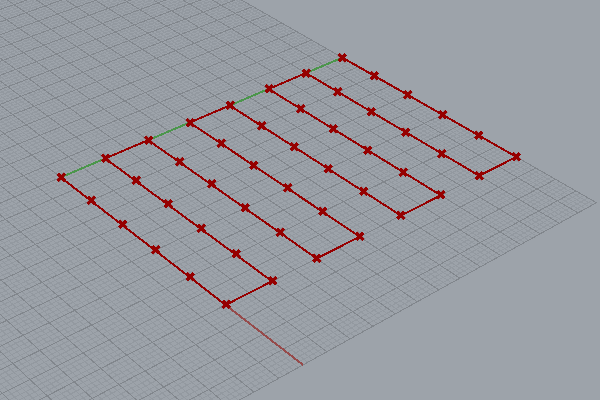
では、順にアルゴリズム作成過程を追ってみましょう。
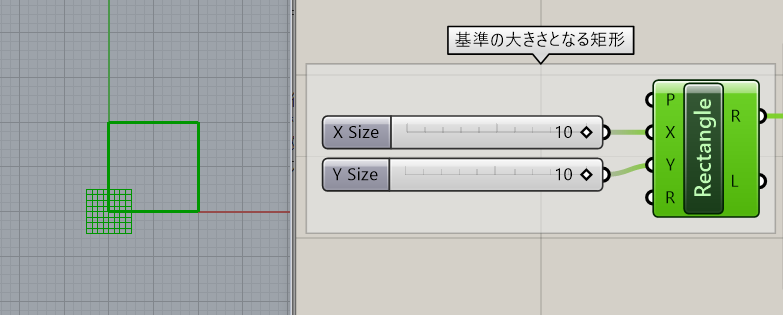
まず[Rectangle]コンポーネントで、矩形を作成します。この矩形がX,Yに隣り合う点同士の距離になります。
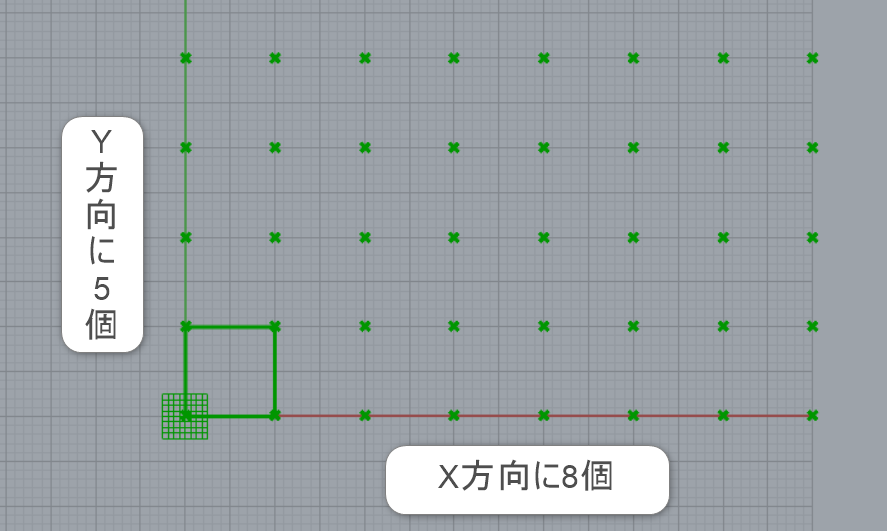
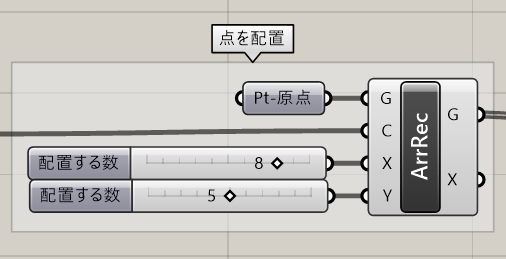
次に原点に配置した点を[Rectangular Array]コンポーネントで矩形上に配列します。X方向、Y方向にそれぞれ配置する数もここで指定します。
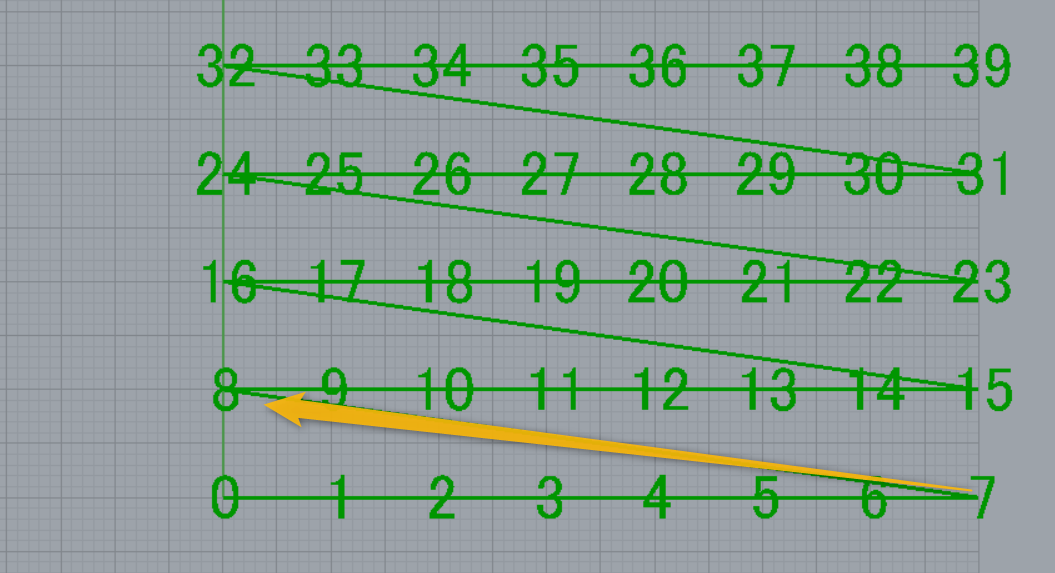
[PolyLine]コンポーネントを繋ぎ、点群を通るポリラインを作成してみます。この時点では最初に意図していた[コの字]に折り返すポリラインが作成できません。これは[PolyLine]コンポーネントはインデックス順に点を繋ぐので、0,1,2,3,4,5,6,7と点を繋いだ後に、8に繋がるためです。

望んだ形で[コの字]にポリラインを引くためには、下の図の様に2列目、4列目、と偶数列の点の並びを反転しないといけません。
この形を再現するために
・奇数列はそのまま変化をさせない
・偶数列は点の並びを反転する
というアルゴリズムを追加してみます。
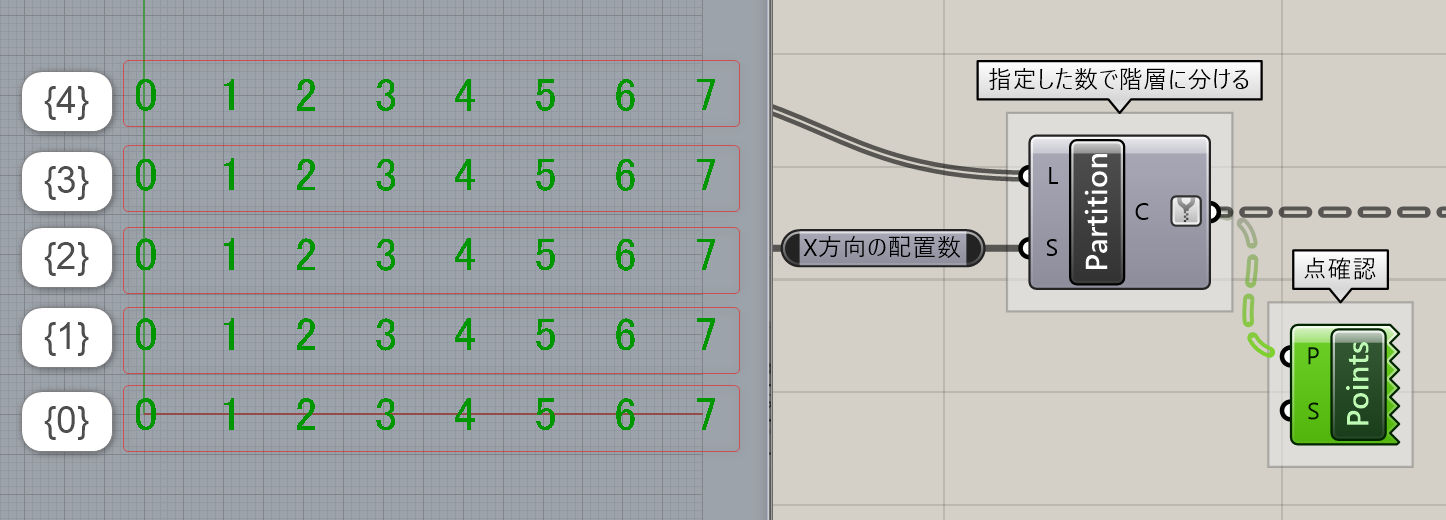
[Partion List]コンポーネントを使って、データを指定した数ずつ階層に分けます。分割する数はX方向の配置数を入力します。X方向の数で階層を分けたため、列ごとに異なる階層に設定することができました。
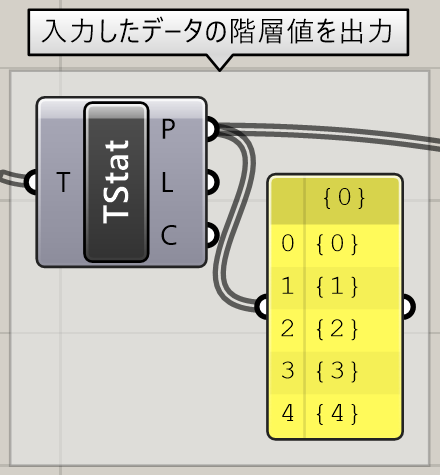
次にこのデータを[Tree Statics]コンポーネントに入力し、データの階層値を取得します。列が5個なので、{0}{1}{2}{3}{4}の計5個の階層値が出力されています。
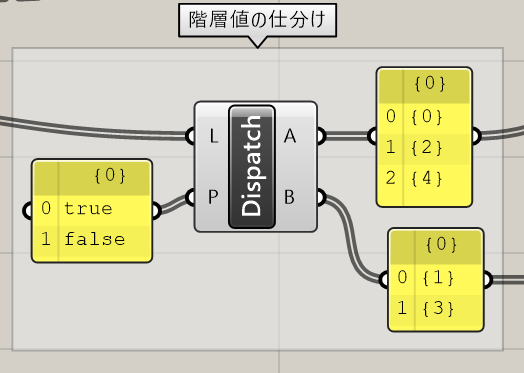
取得した階層値を[Dispatch]コンポーネントに繋ぎ、trueにあたる階層値をA端子から、falseにあたる階層値をB端子から出力します。[Dispatch]はP(Pattern)端子に入れたTrue・Falseの数が足りない場合、最後まで入力したパターンを繰り返します。なので、A端子からは{0}{2}{4}が、B端子からは{1}{3}が出力されます。
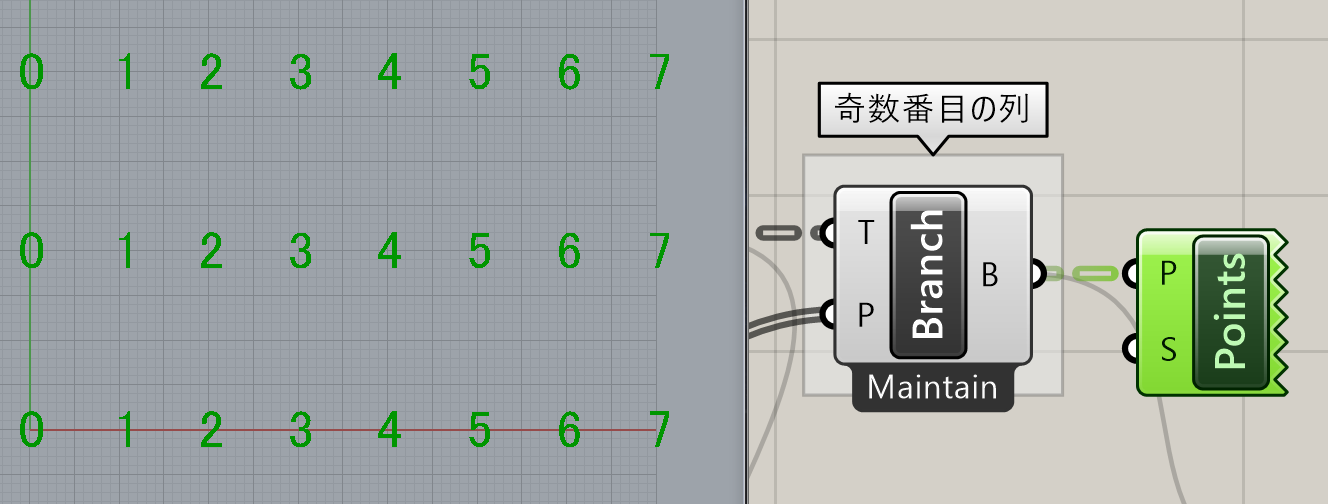
[Tree Branch]コンポーネントで、奇数番目の階層値のデータ、偶数番目のデータをそれぞれ取得することができます。
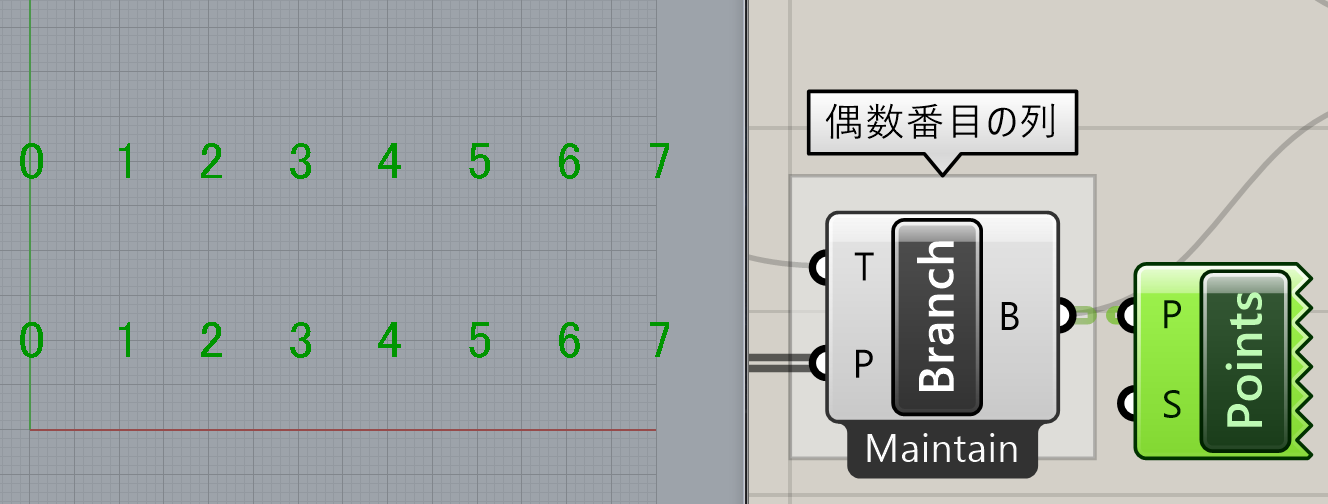
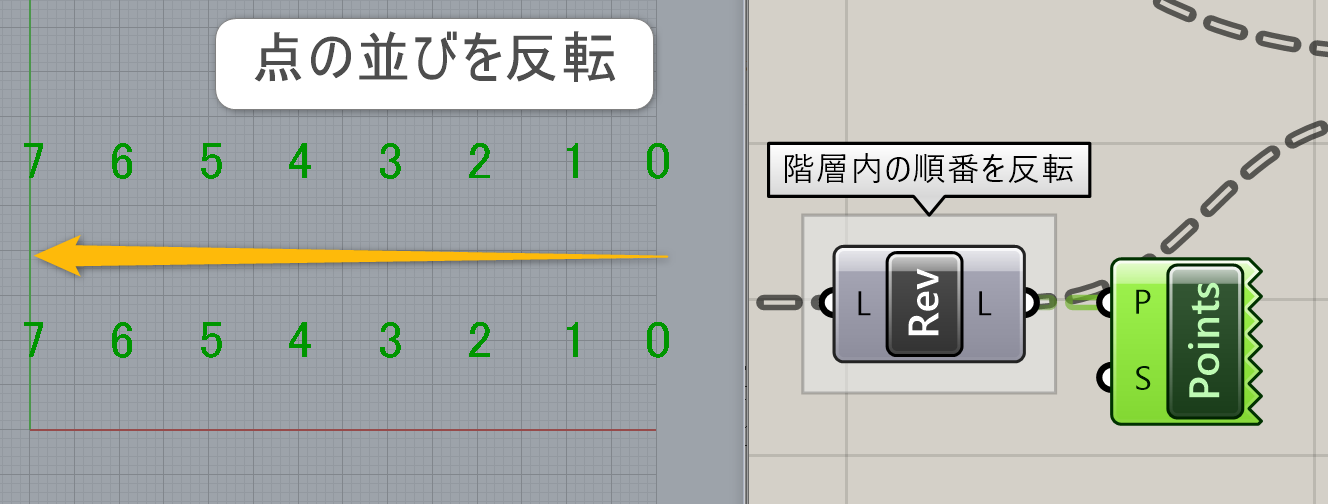
奇数番目には変化を加えず、偶数番目のデータだけ変更します。偶数番目のデータのみ、[Reverse List]コンポーネントで点の順番を反転します。
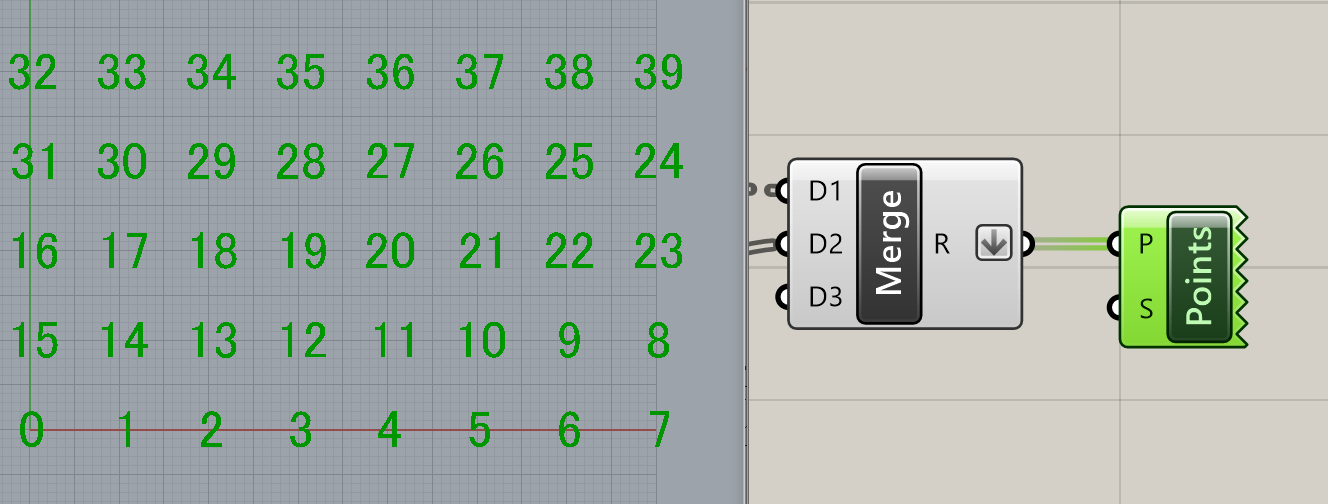
奇数番目、偶数番目のデータを[merge]コンポーネントで、再度まとめます。まとめた後にflattenオプションをつけて階層をなくします。出力を見ると意図した形に点を並び変えることができたのがわかります。
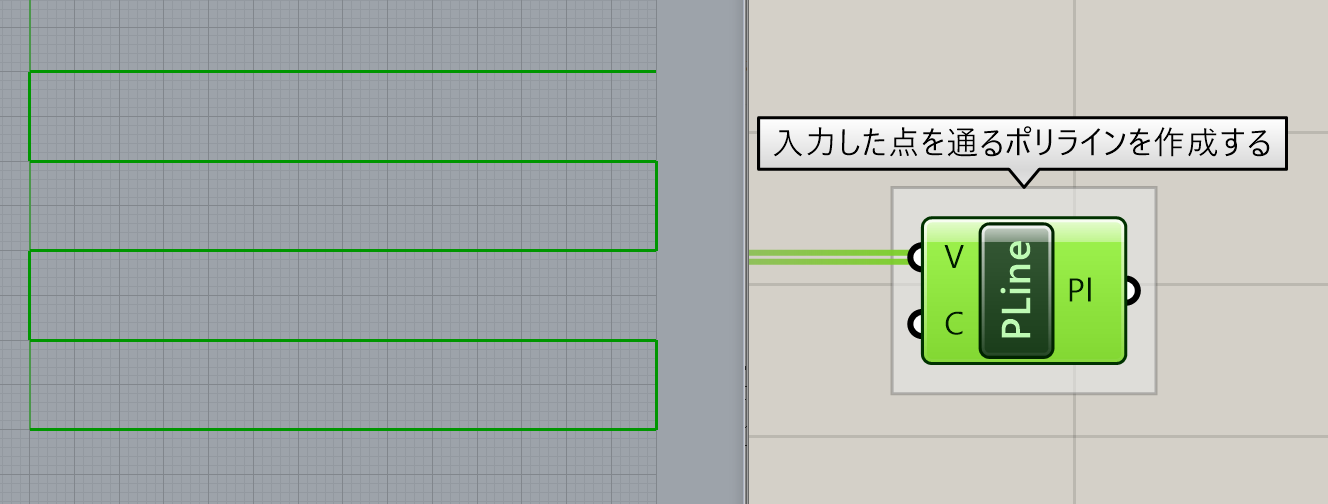
点群を[PolyLine]コンポーネントに繋ぎ、一筆書きの要領でポリラインを作成します。
上記のようなアルゴリズムで、階層ごとに処理を変えて望んだ形を作成するアルゴリズムができました。こういった形でアルゴリズムを作ると、XYの数、間隔を変更しても追従するアルゴリズムが作成できます。
補足1:
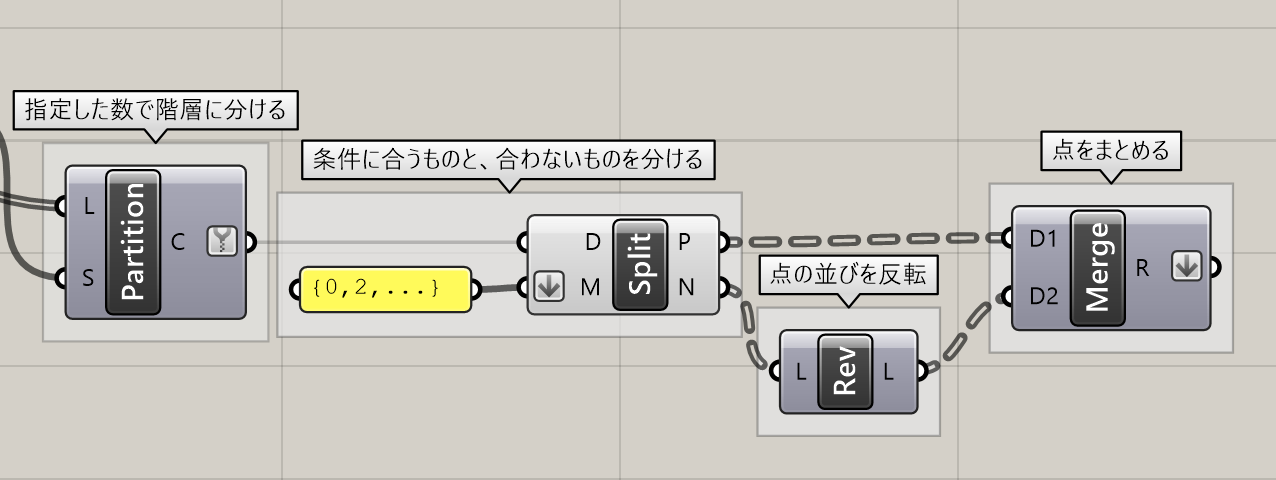
コンポーネント数を少なくアルゴリズムを作成するのであれば、下図のように[Split Tree]を使う方法もあります。
1.[Partition List]で階層ごとに分ける。
2.[Split Tree]でMaskで指定した条件に合うものと、合わないもので分ける。ここでの指定は、0,2,…とすることで、{0},{2},{4}の階層値をP端子から出力。それ以外はN端子から出力。
3.偶数番目の階層のみ、[Reverse List]で点を反転。
4.[Merge]でまとめる。
という流れです。
補足2:
もう少し条件が複雑な[Split Tree]を使った例を見てみます。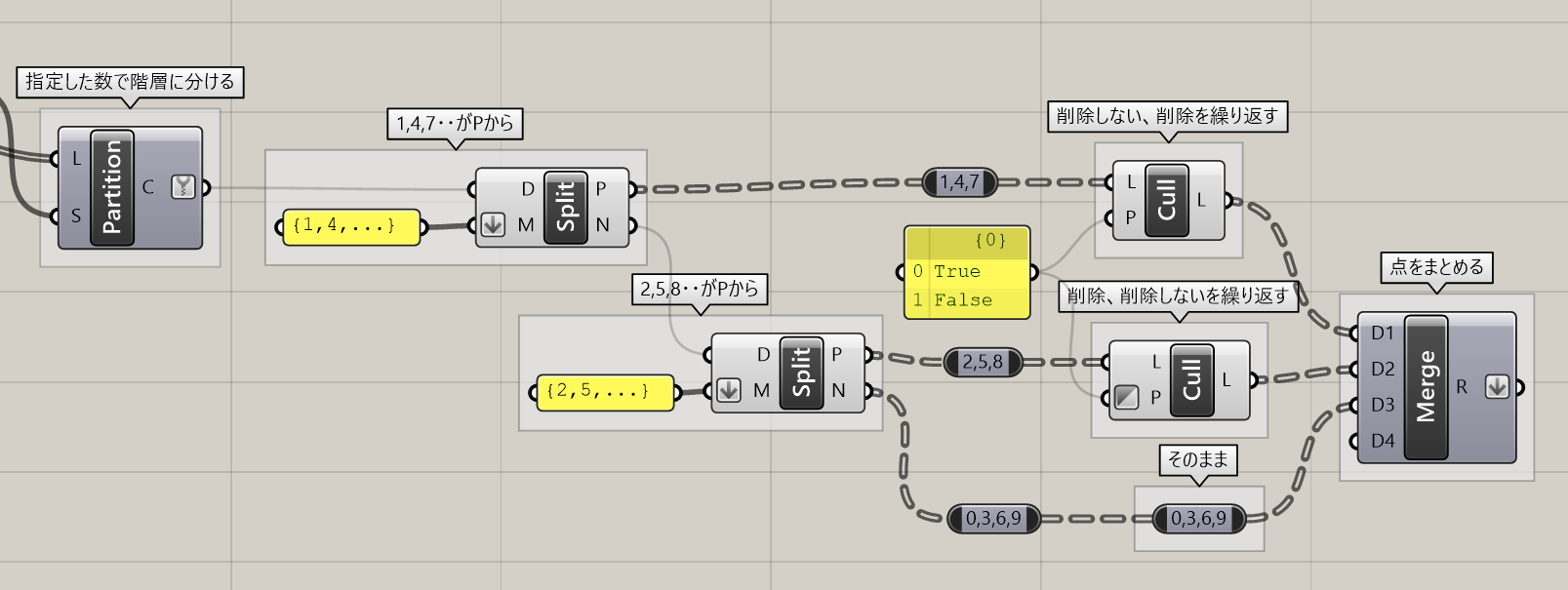
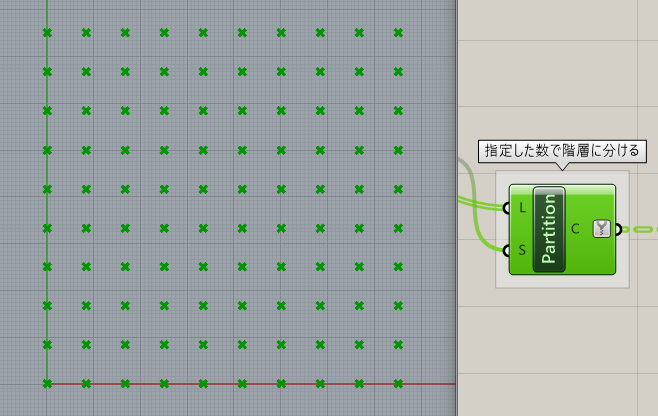
1.[Partition List]で点群を階層ごとに分ける。ここまでは以前と同じアルゴリズムです。
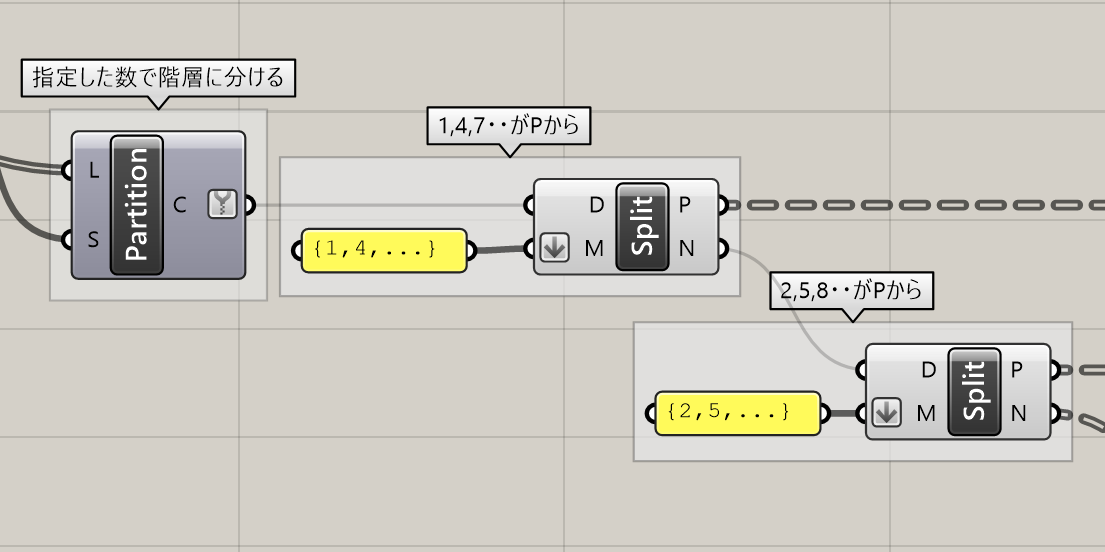
2.[Split Tree]を2回使用し、それぞれの条件に分ける。1回目は、1,4,7,…をPから、それ以外をNから出力。2回目は、2,5,8…をPから、それ以外をNから出力。
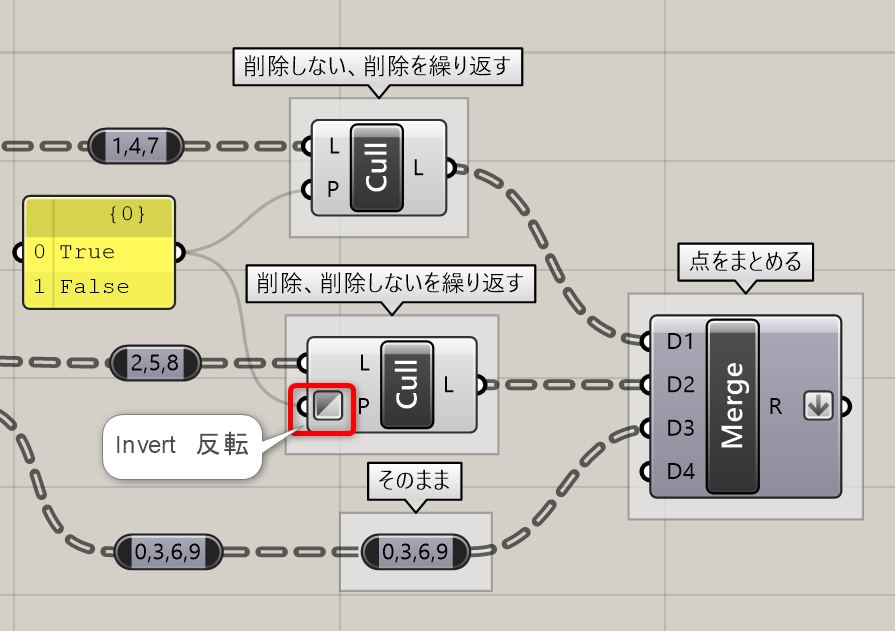
3.[Cull Pattern]を使用して、点を市松模様になるように削除。[Cull Pattern]はFalseにあたるデータを削除するため、1,4,7は削除しない、削除..を繰り返す。2,5,8はInvertオプションを使い、削除、削除しない…を繰り返す。0,3,6,9は変更しない。
最後に[Merge]を使用して、点群をまとめる。
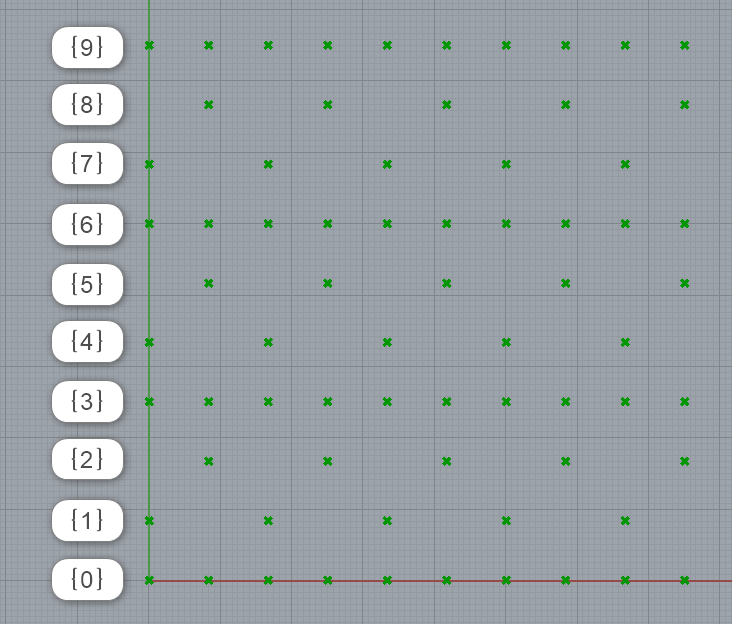
4.結果。{1}{2}の個所が市松模様。{4}{5}、{7}{8}も同様。{0}{3}{6}{9}は変化せず。
こういった形で階層により処理を変えることで、より柔軟にアルゴリズムの処理を変化させることができるようになります。是非、挑戦してみてください。
