Grasshopperでアルゴリズムを作成する際、階層構造を超えてデータを確認したい時に、やむを得ずFlattenして、階層を無くさざるを得ないことがあります。そんな時に[Unflatten Tree]コンポーネントを使うことで、階層構造を元通りにして、アルゴリズムを作成することができます。
- Grasshopperの階層構造を理解し、編集を行っている人向け
- Grasshopperを使ってアルゴリズム作成したい人
- Grasshopper応用
- 簡単な階層構造のリセット
- 階層構造の面倒な編集
- 変更した階層構造を基準に合わせ元通りにします
例えば、下記の様に複数の階層を持った文字列の末尾に通し番号を割り当てたいとします。元の[Text]内は複数階層があるので、Flattenで階層を無くさないと、[Concatenate]で文字を結合できません。
この例では[Concatenate]で文字列を結合後[Unflatten Tree]コンポーネントのTree(T)に、Flattenする前のデータをGuide(G)に入力することで、階層構造をFlattenする前に戻すことができます。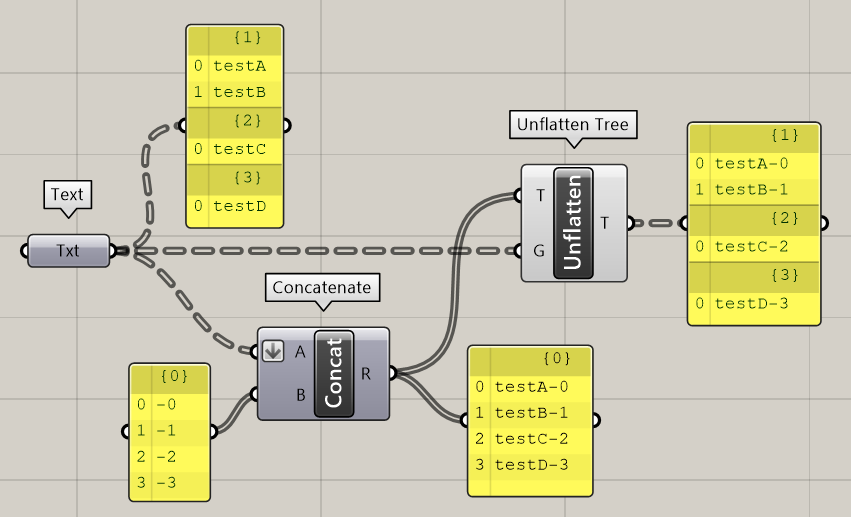
次に、もう少し複雑な例を見てみます。
六角形を用意し、曲線との距離に応じて六角形の頂点が伸び縮みする、というアルゴリズムを考えてみます。
大まかな考え方は、下記となります。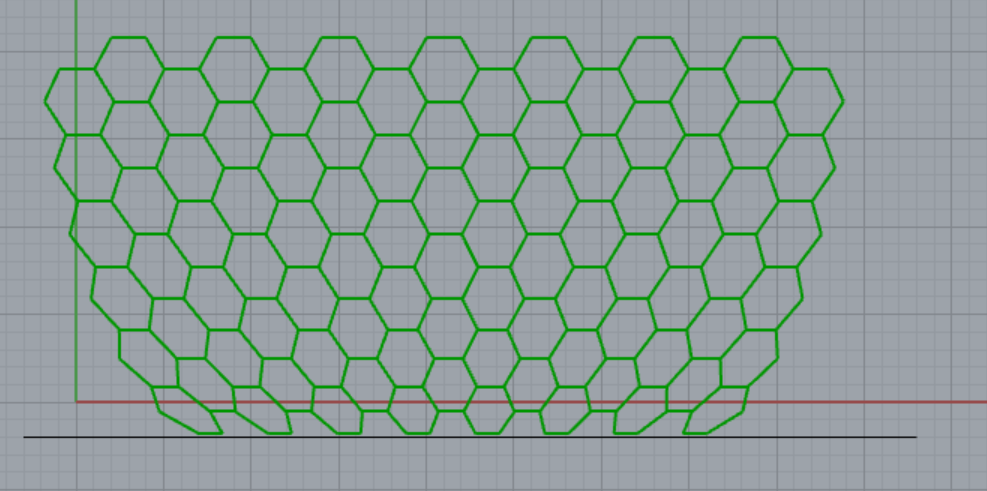
1.[Hexagonal]で六角形作図
2.[Discontinuity]で六角形の各頂点を取得
3.[CurveClosestPoint]で、曲線と2の六角形の頂点とのそれぞれの距離を測る
4.[Bounds]で3で求めた距離の最小から最大の範囲を求める
5.[Remap Numbers]と[Graph Mapper]を使い、適切なスケール値に変化させる
6.[Scale NU]で、頂点座標をXY方向に縮小
7.[PolyLine]で、再度ポリラインを作成する。(クリックで拡大)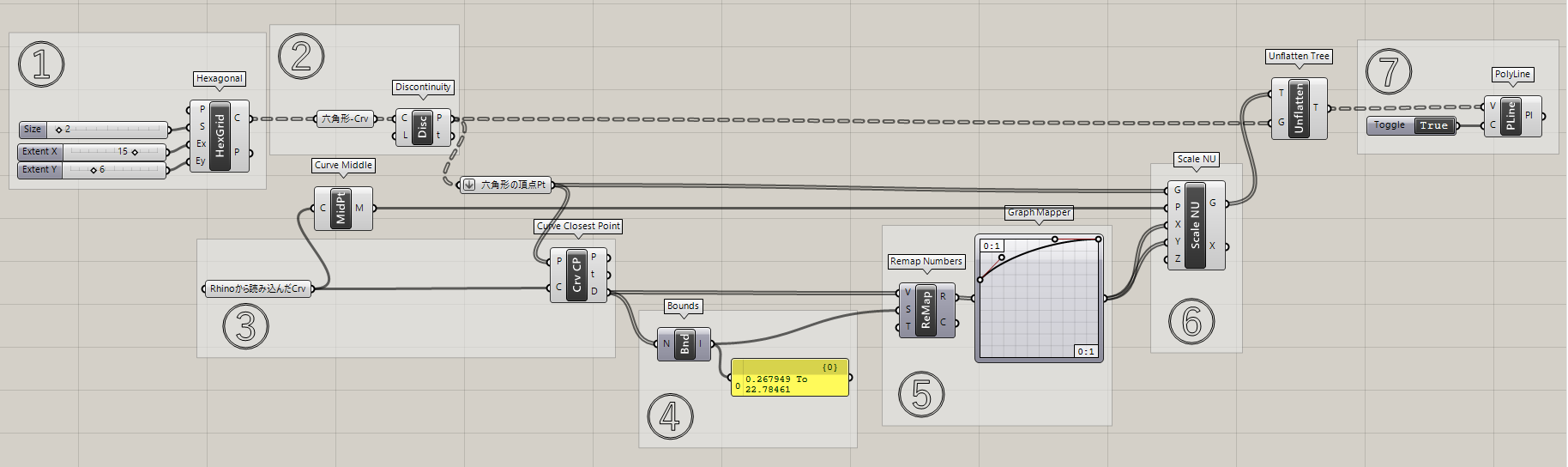
以降、順を追って確認してみます。
左図は、1で作成した六角形。
[Discontinuity]から出力される点は、六角形の各頂点が階層ごとに6つずつ分かれて出力されています(クリックで拡大)。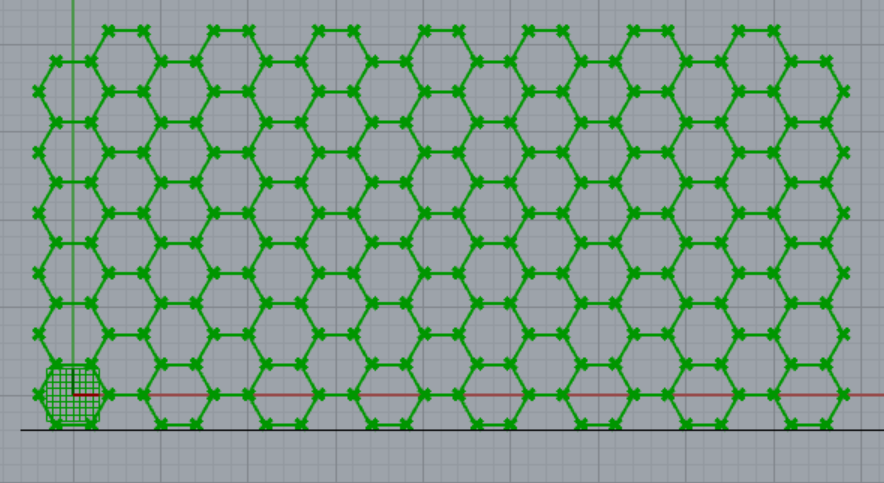
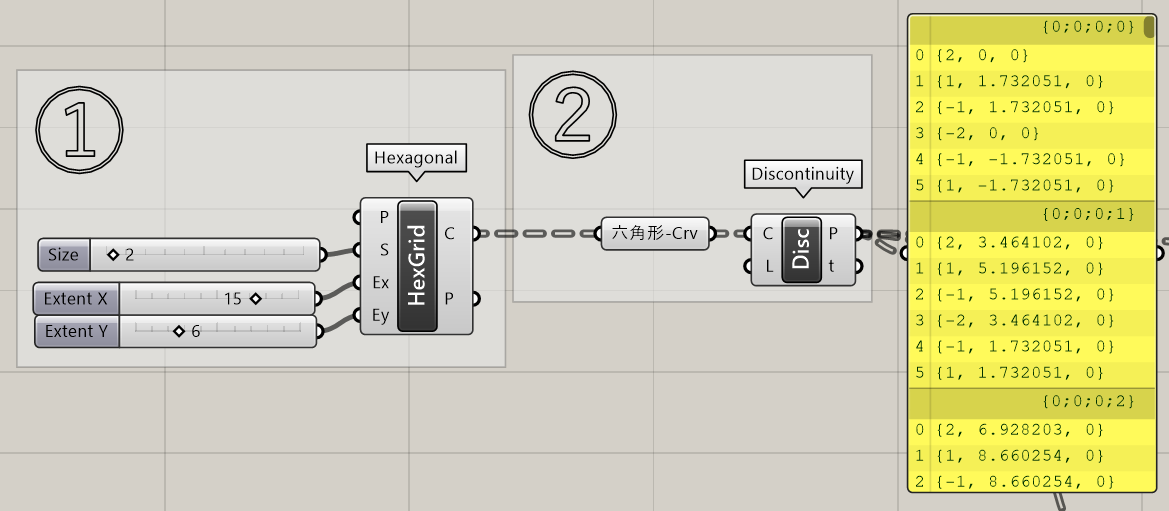
3.[CurveClosestPoint]を使い、Rhinoから読み込んだ曲線と六角形の頂点の距離を求めます。
また後の工程を考え、六角形の頂点をここでFlattenしておきます。Flatten後は、曲線と点の距離も階層がなくなりました。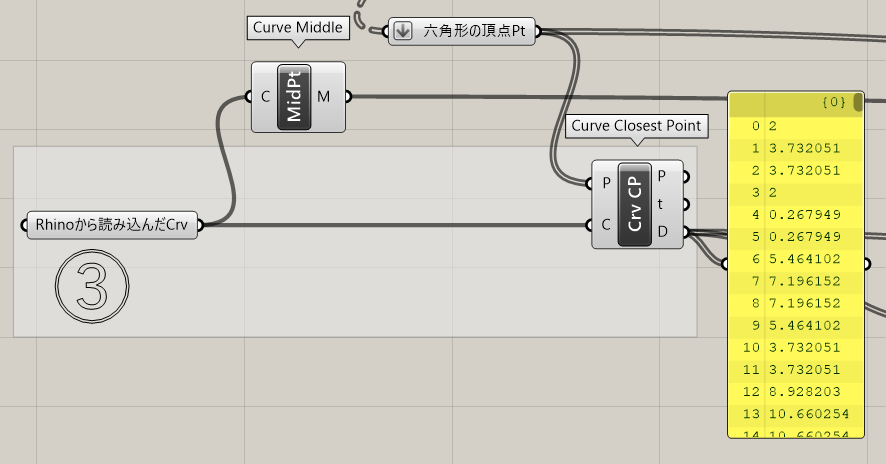
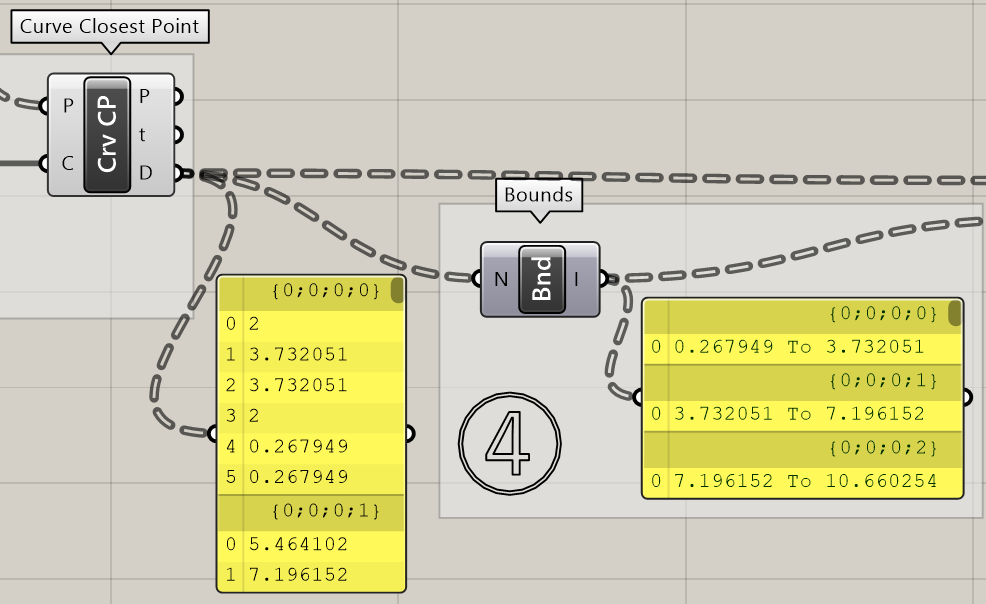
4.曲線と頂点の距離を、[Bounds]で最小から最大の範囲として出力しています(左図)。
Flattenしていないと、各六角形ごとに最小~最大の範囲を出力することになります(右図)。
ここでは複数の六角形を塊として、まとめて頂点を変形したいので、事前にFlattenしておく必要があります。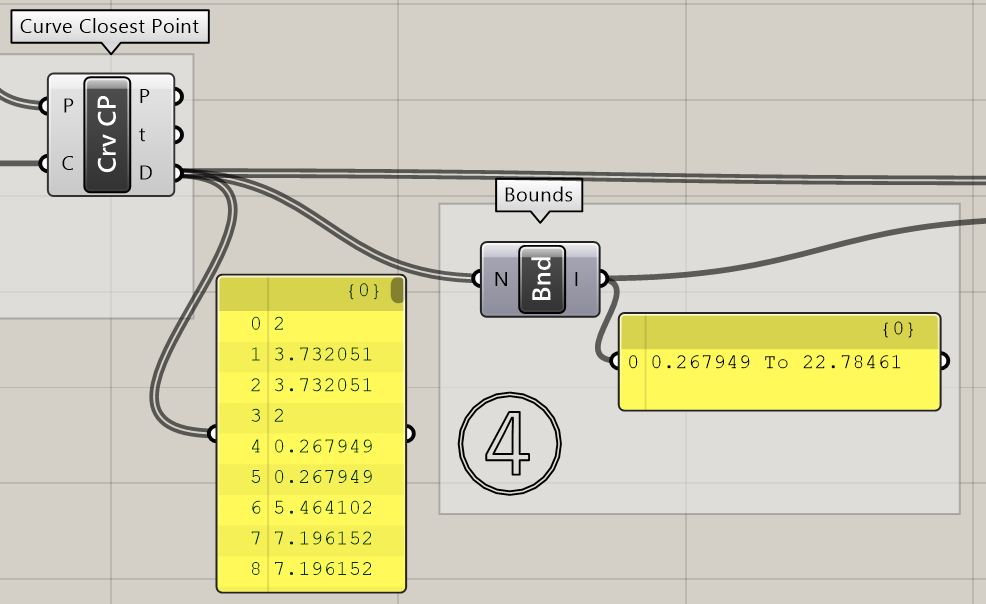
5.[Remap Numbers]で点と曲線の距離を0から1に変換し、[Graph Mapper]で任意の値に変更します。
[Bounds][Remap Numbers][Graph Mapper]は非常によく使う流れなので、詳しくはリンク先の「詳細」からご確認ください。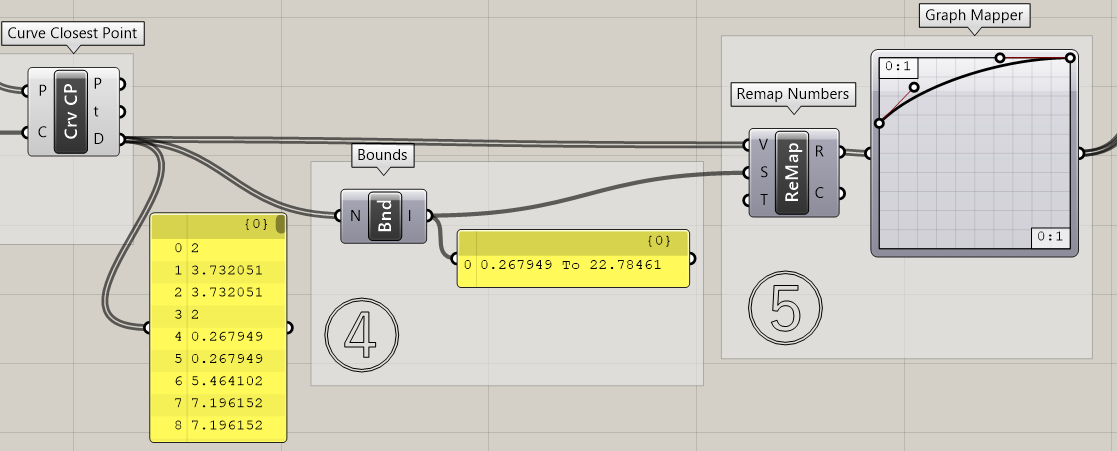
6.[Scale NU]で六角形の頂点を、曲線の中点に近づけた図。
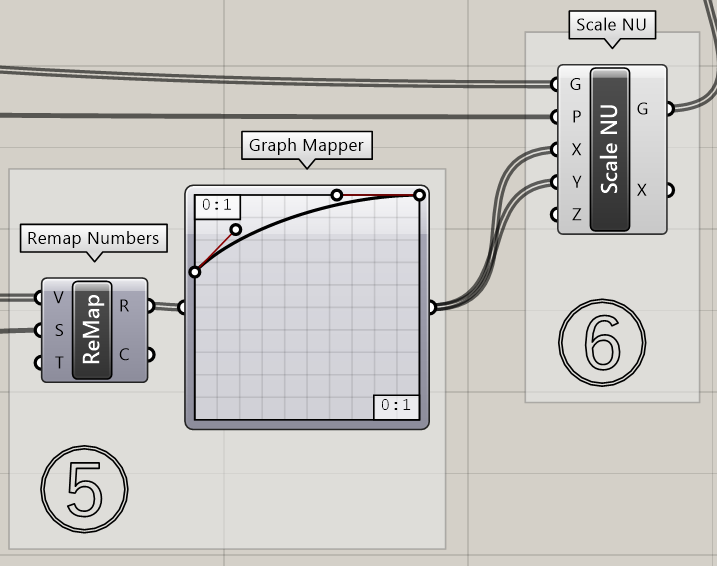
7.[PolyLine]で、六角形の各頂点をつないで一筆書きの要領で、ポリラインを作成したいと思います。
ですがFlattenで階層をなくした状態なので、六角形を作図することができません(左図)。
[Unflatten Tree]を使い、Flattenする前の階層構造に戻すことで、正しく六角形上のポリラインを作成することができます(右図)。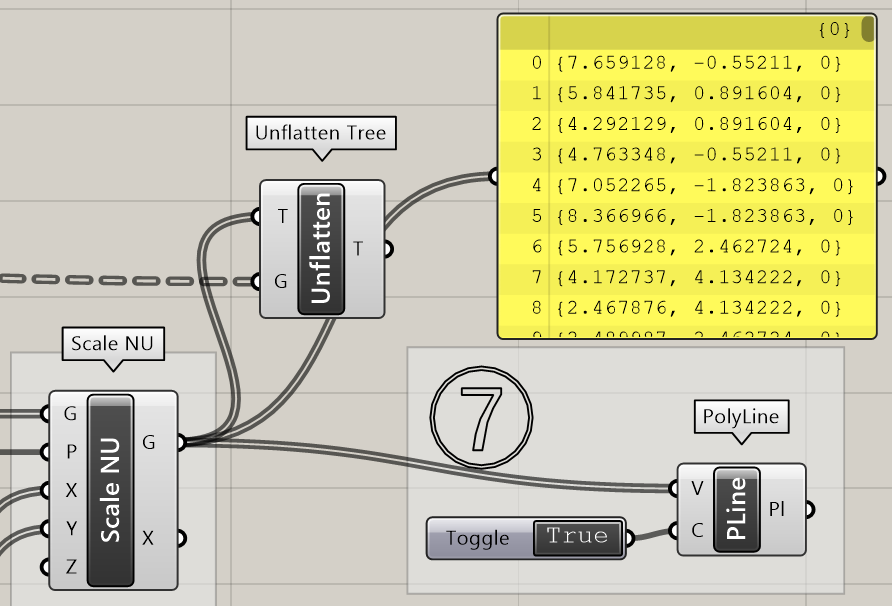
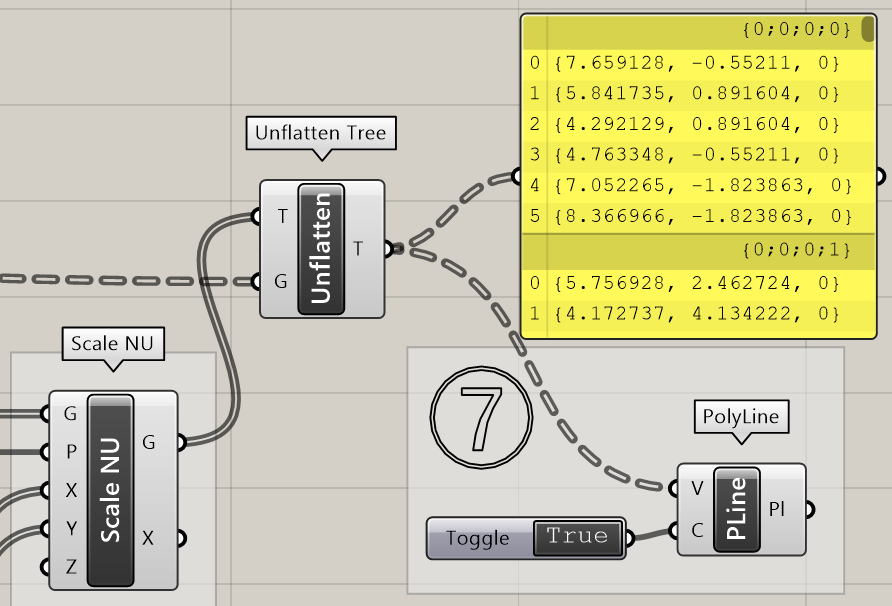
[Unflatten tree]は非常に便利な機能ですが、Treeに入力したデータをGuideに合わせるという仕様上、
TreeとGuideのデータの数が異なる場合はエラーとなります。
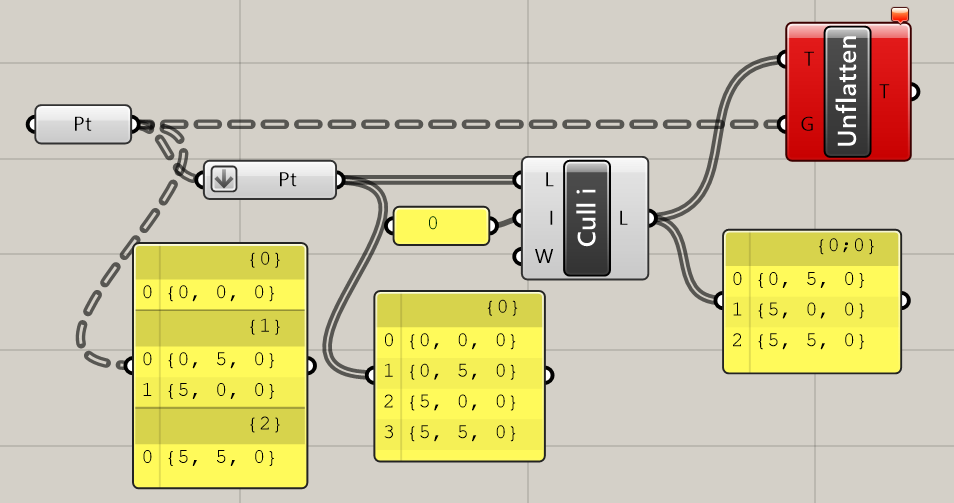
下記は、[Cull Index]で0番に該当するデータを削除したため、[Unflatten Tree]がエラーになった例です。
アルゴリズム作成途中にデータの数を変更しないようにご注意ください。